Vorbemerkung
Dieser einfache Selbsttest aus dem Jahr 2001 enthält 7 Fragen, die entwickelt wurden, um angehenden Informatikstudierenden ein Gefühl zu vermitteln, mit welchen Fragen man sich im Studium beschäftigen wird. Dabei wurden die Aufgaben so formuliert, dass keine Fähigkeiten vorausgesetzt werden, die man erst im Studium erlernen muss. Vielmehr handelt es sich um Grundfertigkeiten (man könnte auch Talent dazu sagen), die man als Informatiker haben sollte, um erfolgreich das Studium zu absolvieren.
Nimm dir in etwa eine Stunde Zeit, um die Aufgaben zu lösen. Falls die gefundenen Ergebnisse sehr stark von den Lösungsvorschlägen abweichen oder bei einer Aufgabe kaum eine Lösung zustandekommt, solltest du zumindest eine ausführliche Studienberatung in Anspruch nehmen und möglicherweise die Studienwahl noch einmal überdenken. Eventuell hilft auch ein weiterer Selbsttest (wieder verfügbar ab Ende März 2023) auf der Webseite der Fakultät Informatik.
Es seien drei Typen von Bauelementen gegeben.
 "Beide":
"Beide":- wenn genau an beiden Eingängen Strom anliegt, produziert der Ausgang Strom.
 "Einer reicht":
"Einer reicht":- sobald an einem Eingang Strom anliegt, produziert der Ausgang Strom.
 "Umkehr":
"Umkehr":- liegt am Eingang Strom an, so liegt keiner am Ausgang an; liegt am Eingang kein Strom an, so liegt er am Ausgang an.
1a) Leuchtet die Glühlampe in folgender Schaltung?
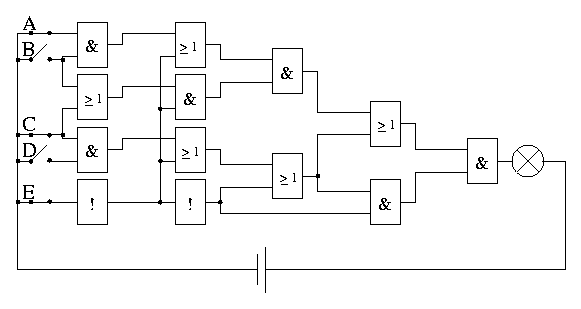
1b) Welche Bauelemente müssen in der folgenden Schaltung verwendet werden, um zu erreichen, dass die Lampe nur dann leuchtet, wenn folgendes gilt:
- Schalter C (als Notschalter) muss immer auf Aus stehen und
- entweder Schalter A und B gleichzeitig auf An stehen
- und/oder Schalter D und E gleichzeitig auf An stehen.
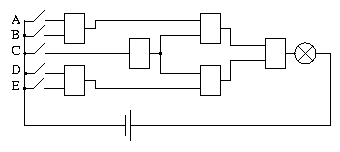
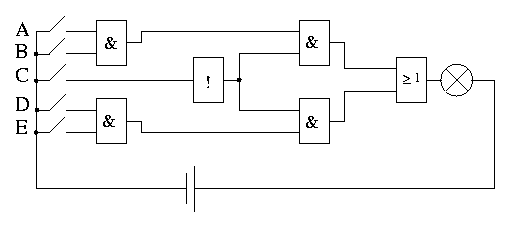
Mit dieser Aufgabe soll logisches Denkvermögen und die Fähigkeit, parallele Probleme zu erfassen, getestet werden.
Es empfiehlt sich, in der Grafik zu markieren, an welcher Stelle Strom anliegt und wo nicht. Dazu kann man entweder Farbe verwenden oder an die entsprechenden Leitungen eine Markierung setzen (1=Strom, 2=kein Strom).
Dann betrachtet man jedes der Bauelemente von den ersten Eingängen (links) bis zum letzten Ausgang (rechts) und ermittelt aufgrund der Werte, die an den Eingängen anliegen die Ausgangsbelegung anhand der Beschreibung.
In der folgenden Grafik ist eine Leitung mit Strom rot markiert, Leitungen ohne Strom sind schwarz. Daraus resultiert, daß die Lampe leuchtet.
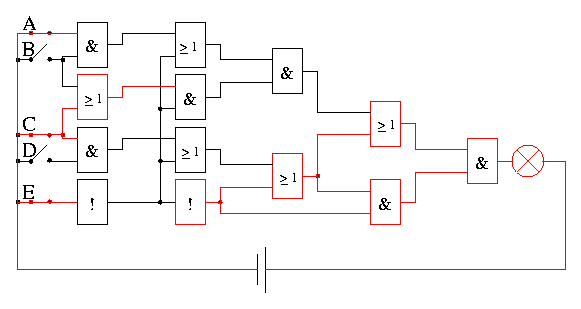
Da Schalter A und Schalter B beide gleichzeitig angeschaltet sein müssen, wird dies mit Hilfe eines Beide-Bauelements zu einer Information zusammengefaßt, die angibt, ob beide Schalter aktiv sind.
Analog gilt dies für die Zusammenfassung des Stromes von Schalter D und E.
Der Strom darf nun nur dann weiterfließen, wenn Schalter C keinen Strom durchläßt. Es gibt nun kein Bauelement, welches nur dann Strom produziert, wenn an einem Eingang Strom anliegt und an dem anderen nicht. Daher muß ein Trick verwendet werden und der Stromfluß von Schalter C umgekehrt werden, bevor es mit den Strömen zusammengefaßt werden, die von den ersten beiden Bauteilen produziert werden.
Aus dem umgekehrten C und den beiden Zwischenströmen werden zwei neue Zwischenströme generiert, wenn Zwischensignal und das umgekehrte C Strom führen.
Schließlich reicht es aus, wenn eines der beiden letzten Zwischensignale aktiv ist, um die Lampe zum Leuchten zu bringen.
Es gibt eine Gruppe von Personen. Einige kennen sich gut und erzählen einander jedes Geheimnis, andere können sich nicht leiden und reden nicht miteinander. Folgende Personen sind insgesamt bekannt: Guido, Gudula, Wolf, Petr, Peter, Werner, Winfried, Dieter, Wolfgang, Uwe, Hanno, Andreas.
Kann nun ein Geheimnis, welches Guido kennt, zu Hanno durchdringen, wenn folgende Beziehungen gelten?
- Guido spricht nur mit Petr und Gudula
- Gudula spricht nur mit Wolf und Guido
- Wolf spricht nur mit Peter und Gudula
- Petr spricht nur mit Guido, Wolfgang und Peter
- Peter spricht nur mit Wolf, Petr, Wolfgang, Werner, Winfried und Dieter
- Werner spricht nur mit Peter und Winfried
- Winfried spricht nur mit Peter und Werner
- Dieter spricht nur mit Wolfgang, Hanno und Peter
- Wolfgang spricht nur mit Petr, Peter, Uwe und Dieter
- Uwe spricht nur mit Wolfgang und Andreas
- Hanno spricht nur mit Andreas und Dieter
- Andreas spricht nur mit Hanno und Uwe
Was ist der kürzeste Weg (die wenigsten Personen, die das Geheimnis weitersagen müssen) von Werner zu Andreas?
Diese Frage soll testen, wie gut man konkrete Probleme abstrahieren und die dahinter verborgene Struktur modellieren kann.
Die hier genannten Personen bilden ein Netzwerk aus, in dem die Informationen verbreitet werden. In der Informatik nennt man eine solche Struktur Graph.
Die Personen stellen Kommunikationspunkte (Knoten) dar, die entweder verbunden sind oder auch nicht. Die Informationen können nur entlang einer Verbindung (Kante) wandern.
Mit diesem Wissen läßt sich ein Bild zeichnen.
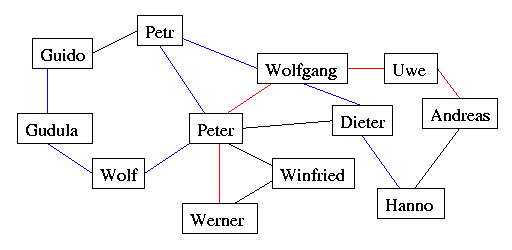
In dieser Grafik kann man nun entlang dieser Kanten wandern und dabei den Weg markieren. Eine mögliche Lösung der ersten Teilaufgabe ist blau gekennzeichnet. (Es gibt noch eine zweite, die hier nicht verraten wird ;-)
Die Lösung der zweiten Teilaufgabe - in rot gekennzeichnet - findet man intuitiv, indem man zuerst irgendeinen Weg sucht und diesen dann schrittweise verbessert, bis kein besserer zu finden ist. Dieses Verfahren führt wahrscheinlich nicht immer zur besten Lösung. Welches geeignetere Verfahren man verwenden kann, wird man im Studium lernen. (Auch hier gibt es eine 2. Lösung, die man leicht anhand des Bildes ersehen kann.)
Für einen Dachstuhl müssen Holzbalken zurechtgesägt werden. Dabei werden Balken zu 10 m Länge geliefert. Benötigt werden folgende Zuschnitte:
- 1 mal 5 Meter
- 2 mal 2 Meter
- 3 mal 6 Meter
- 4 mal 3 Meter
- 6 mal 1 Meter
3a) Wieviele 10-m-Balken müssen gekauft werden?
3b) Wie werden die Schnitte gesetzt?
Diese Aufgabe stellt ein Optimierungsproblem dar für das es ein Lösungsverfahren zu ermitteln gilt, damit möglichst wenig Holz gekauft werden muß.
Eine optimale Lösung für diese recht einfach wirkende Problem besteht aus einem Verfahren, welches sehr aufwändig ist. Daher soll an dieser Stelle nur ein Näherungsverfahren vorgestellt werden, welches noch immer gute Resultate liefert, aber nicht immer das bestmögliche Ergebnis erzeugt. (In diesem Beispiel aber schon.)
Man sollte mit dem Zuschnitt der größeren Stücke beginnen, damit aus den Reststücken die kleineren Teilstücke hergestellt werden können.
Zuerst sortiert man die Schnittaufträge der größe nach, beginnend mit dem Größten.
- 3 mal 6 Meter
- 1 mal 5 Meter
- 4 mal 3 Meter
- 2 mal 2 Meter
- 6 mal 1 Meter
Im ersten Schritt nehmen wir einen neuen Balken und schneiden daraus das größte herzustellende Teilstück heraus. Der Rest wird aufgehoben.
Von nun an wird geprüft, ob aus den Reststücken mindestens eins ausreichend lang ist, um daraus das aktuelle Teilstück zu sägen. Wenn es solchte Reste gibt, so nehmen wir das kleinste dieser. Ansonsten wird ein neuer Balken zersägt.
Daraus ergibt sich folgende Lösung, wobei die Reihenfolge der zu schneidenden Teilstücke angegeben ist:
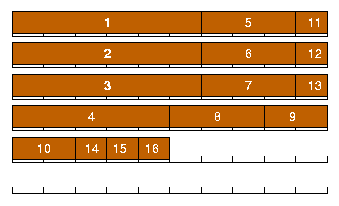
Beim Surfen im Internet stellen Sie fest, daß die Webseiten nicht schnell genug angezeigt werden. Sie nutzen derzeit einen Athlon Prozessor mit 2,1 GHz, 512 MB Arbeitsspeicher und ein 56k-Modem an einem analogen Telefonanschluß. Wie könnte man erreichen, daß die Webseiten schneller angezeigt werden?
- eine schnellere Pentium IV CPU einbauen
- mehr Arbeitsspeicher einbauen
- ein Internetmodem verwenden
- einen anderen Provider nehmen
- das Laden von Bildern deaktivieren
Als Informatiker muß man oft Probleme lösen, die im Spannungsfeld zwischen Wirtschaft und Technik liegen. Wer zu sehr auf Schlagwörter vertraut oder gar den Versprechungen der Werbung blind glaubt, verschleudert schnell viel Geld. Am Anfang sollte daher eine gründliche Überlegung stehen warum denn die Webseiten nicht schnell genug angezeigt werden:
Normale Webseiten erfordern nur relativ wenig Aufwand um ihre Darstellung zu berechnen, extrem aufwändige Seiten hingegen können die CPU sehr belasten. Der angegebene Prozessor ist allerdings leistungsfähig genug um auch komplexere Seiten aufzubereiten - also wird der Einbau einer schnelleren CPU wahrscheinlich keine Geschwindigkeitszuwächse bringen.
Etwas Ähnliches gilt für die Größe des Arbeitsspeichers: Mit 512 MB ist dieser groß genug für das Betrachten der allermeisten Webseiten. Lediglich wenn neben dem Webbrowser noch andere Programme ausgeführt werden, die viel Arbeitsspeicher verlangen, kann ein Ausbau Geschwindigkeitsvorteile bringen.
Wenn nun der Rechner schnell genug ist, könnte noch eine zu langsame "Anlieferung" der Daten die Anzeige der Webseiten bremsen. Allerdings ist die Antwortmöglichkeit "ein Internetmodem einbauen" keine besonders "expertentaugliche" Antwort, da der Begriff "Internetmodem" überhaupt nichts über die real genutzte Geschwindigkeit aussagt. Zuerst wäre zu klären was denn das für ein Gerät ist und was er wirklich kann.
Genauso ist es grundsätzlich nicht richtig zu meinen, ein anderer Provider wäre schneller. Wenn der Provider die Daten schneller liefert als sie das Modem auf den Rechner übertragen kann, würde ein Providerwechsel nichts erreichen. Ebensowenig kann der Provider verantwortlich gemacht werden, wenn schon der Rechner von dem die Daten geholt werden sollen, nicht schnell genug ist.
Ein guter Tipp ist jedoch meist das Abschalten der Anzeige der Bilder. Zwar sieht man dann nicht mehr die ganze Webseite, dafür müssen aber auch viel weniger Daten (Bilder brauchen erheblich mehr Übertragungszeit als einfacher Text) übertragen und dargestellt werden. ;-)
In einem Haus hängen auf dem Dachboden drei Glühbirnen (wobei man davon ausgehen kann, dass sie funktionieren und ausgeschaltet sind). Die dazugehörigen Schalter befinden sich aufgrund eines Designfehlers im Keller. Es ist leider auch nicht bekannt, welcher Schalter zu welcher Glühbirne gehört. Der Hausbesitzer - ein ausgesprochen fauler Informatiker ;-) - möchte mit möglichst wenig Aufwand herausfinden, welcher Schalter welche Glühbirne bedient.
Er befindet sich im Keller und will nur ein einziges mal die lange Treppe bis auf den Dachboden steigen. Wie kann er trotzdem die Zuordnung zwischen den Schaltern und Glühbirnen herausfinden? Dabei hilft ihm keine andere Person, es sind keine technischen Hilfsmittel erlaubt, der Keller hat keine Fenster und darf nicht noch einmal betreten werden nach Verlassen.
Mit dieser Aufgabe soll getestet werden, wie gut man in der Lage ist, einen Situation vollständig zu erfassen. Gerade bei dieser Aufgabe sieht man schön, daß man beim Modellieren der Welt oft wichtige Attribute übersieht.
Ganz offensichtlich ist die Tatsache, dass eine Glühbirne Licht erzeugt, so lange Strom hindurchfließt. Doch damit kann nur einem Schalter eine Glühbirne zugeordnet werden. Es fehlt also eine Mlöglichkeit, die letzten beiden Schalter zuzuordnen.
Beim ganaueren Überlegen fällt auf, daß eine Lampe noch ein weiteres Attribut hat, welches vom Stromfluß abhängig ist: Die Temperatur. Glühlampen, durch die Strom fließt, werden heiß. Lampen, durch die vor kurzer Zeit Strom geflossen ist, sind warm.
Damit ergibt sich eine recht einfache Lösung:
- die ersten beiden Schalter anschalten
- 2-3 Minuten warten
- den zweiten Schalter wieder ausschalten
- so schnell wie moeglich auf den Dachboden laufen
- die beiden dunklen Lampen vorsichtig mit der Hand auf Wärme testen
- Die leuchtende Lampe wird von Schalter 1 geschalten
- Die dunkle aber warme Lampe wird von Schalter 2 geschalten
- Die dunkle aber kalte Lampe wird von Schalter 3 geschalten
Die Funktion der Fibonacci-Zahlen ist folgendermaßen definiert:
| f(n)={ | 1 | n=1 oder n=2 | |
| f(n-1)+f(n-2) | sonst |
Bestimmen Sie den Wert von f(7).
Diese Frage zielt auf das Verständnis für rekursive Darstellung mathematischer Folgen.
Die Berechnung des Wertes kann auf zwei Weisen erfolgen. Die eine Version arbeitet streng nach Vorschrift die entsprechenden rekursiven Aufrufe ab, die zweite Version baut eine Tabelle mit Zwischenwerten auf, um so den Rechenaufwand zu reduzieren.
Version 1
Die Berechnung von f(7) wird laut Vorschrift als f(6)+f(5) ausgeführt.
f(6) ist f(5)+f(4)
f(5) ist f(4)+f(3)
Also ist f(7) = (f(5)+f(4)) + (f(4)+f(3))
daraus folgt f(7) = ((f(4)+f(3)) + (f(3)+f(2))) + ((f(3)+f(2)) + f(2)+f(1))
daraus folgt f(7) = (((f(3)+f(2))+(f(2)+f(1))) + ((f(2)+f(1))+1) + (((f(2)+f(1))+1) + 1+f(1)))
daraus folgt f(7) = ((((f(2)+f(1))+1+(1+1)) + (1+1)+1) + (((1+1)+1) + 1+f(1)))
daraus folgt f(7) = ((((1+1)+1+(1+1)) + (1+1)+1) + (((1+1)+1) + 1+f(1)))
daraus folgt f(7) = 13
Version 2
| n | f(n) |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2* |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
*) Ab hier immer Summe der beiden vorhergehenden Zeilen.
Ein Programmiersystem besteht aus den folgenden Befehlen:
| AUSGABE x | gibt x auf den Bildschirm aus | |
| WENN x MACHE y | sofern x eine wahre Aussage enhält, wird y ausgeführt | |
| GEHE ZU x | setzt die Ausführung an Zeile x fort | |
| (x und y können einfache Variablen, Ausdrücke oder wieder Befehle sein) | ||
Ein Programm besteht aus numerierten Zeilen. Diese enthalten nun die oben genannten Befehle oder auch mathematische Ausdrücke der Form variable := ausdruck. Ein math. Ausdruck kann z.Bsp.: eine einfache Zahl, eine math. Operation (1+2, 3*x, ...) oder auch ein Vergleich (1<2, 2=x, ...) sein.
Wie kann man damit ein Programm realisieren, welches 5 mal in Folge "Hallo Uni" ausgibt, ohne einfach 5 mal den Befehl AUSGABE "Hallo Uni" hinzuschreiben.
Programme schreiben ist nur eine von vielen Fähigkeiten, die ein Informatiker kennen muß. Zumeist werden auch keine Industrie-Programmiersprachen verwendet, sondern akademische Sprachen, die erfunden wurden, um einen bestimmten Sachverhalt darzustellen.
Bevor man ein Programm schreiben kann, muß man sich erst im Klaren sein, auf welche Weise man das Problem überhaupt lösen möchte. Diese Lösungsvorschrift nennt man Algorithmus. Sobald man festgelegt hat, welche Sprache man nutzt, weiß man auch, welche Befehle man für sein Programm verwenden kann.
Um nun 5 mal nacheinander den Text auszugeben, ist es nun möglich, den Ausgabebefehl solange zu wiederholen, bis man genug Text ausgegeben hat. Dazu verwendet man einen Datenspeicher, der die Anzahl der bereits ausgegebenen Zeilen enthält. Anfägnlich ist natürlich noch keine Zeile ausgegeben und man setzt den Zahlenspeicher auf den Wert Null.
1 anzahl := 0
Nun kann man den Text einmal ausgeben:
2 Ausgabe "Hallo Uni"
Nachdem man nun den Text einmal ausgegeben hat, muß man den Zähler um 1 erhöhen. Dazu nimmt man den alten Zählerstand, addiert 1 hinzu und speichert den Wert wieder ab:
3 anzahl := anzahl +1
Nun kann es sein, daß man noch nicht genug Zeilen ausgegeben hat. Ist dies der Fall, so muß man erneut in Zeile 2 gehen, um von dort ab die nächste Zeile auszugeben und die Anzahl wieder erhöhen um danach wieder vergleichen zu können....
4 Wenn anzahl < 5 mache: Gehe zu 2
Ist die anzahl bereits größer oder gleich 5, dann wird nicht mit Zeile 2 fortgesetzt und das Programm ist beendet.
Das gesamte Programm sieht also folgendermaßen aus:
1 anzahl := 0 2 Ausgabe "Hallo Uni" 3 anzahl := anzahl +1 4 Wenn anzahl < 5 mache: Gehe zu 2

