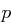 , so dass
, so dass 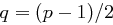 ebenfalls eine ungerade Primzahl ist. (Dieses ist nicht trivial!) Weiter werden zwei primitive Elemente
ebenfalls eine ungerade Primzahl ist. (Dieses ist nicht trivial!) Weiter werden zwei primitive Elemente 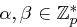 gewählt, mit
gewählt, mit 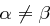 . Der Wert
. Der Wert 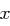 mit
mit 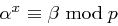 bleibt geheim, die anderen Daten sind öffentlich.
bleibt geheim, die anderen Daten sind öffentlich.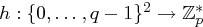 ist definiert als
ist definiert als
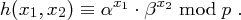
| Hashverfahren | Extension von Hashfunktionen |
Diese Hashfunktion beruht auf dem Diskreten Logarithmus Problem.
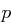 , so dass
, so dass 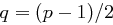 ebenfalls eine ungerade Primzahl ist. (Dieses ist nicht trivial!) Weiter werden zwei primitive Elemente
ebenfalls eine ungerade Primzahl ist. (Dieses ist nicht trivial!) Weiter werden zwei primitive Elemente 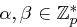 gewählt, mit
gewählt, mit 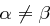 . Der Wert
. Der Wert 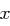 mit
mit 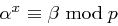 bleibt geheim, die anderen Daten sind öffentlich.
bleibt geheim, die anderen Daten sind öffentlich.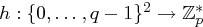 ist definiert als
ist definiert als
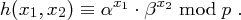
Für diese Hashfunktion ist es vermutlich schwer, Kollisionen zu finden, wie der folgende Satz zeigt.
Satz 14
Wenn eine Kollision für die Chaum-van Heigst-Pfitzmann Hashfunktion 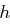 gegeben ist, dann ist der diskrete Logarithmus
gegeben ist, dann ist der diskrete Logarithmus 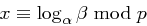 effizient berechenbar.
effizient berechenbar.
Beweis Gegeben ist eine Kollision, also zwei Paare 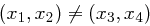 mit
mit
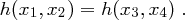

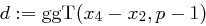 . Aus
. Aus 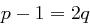 und
und 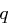 prim folgt
prim folgt 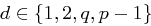 . Entsprechend den möglichen Werten von
. Entsprechend den möglichen Werten von 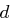 unterscheiden wir vier Fälle.
unterscheiden wir vier Fälle.
Fall 1: Sei 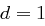 . Dann existiert das Inverse
. Dann existiert das Inverse 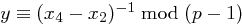 und es folgt
und es folgt
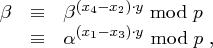
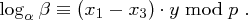
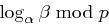 zu bestimmen, in diesem Fall also mit dem erweiterten Euklidischen Algorithmus lösen (Bestimmung von
zu bestimmen, in diesem Fall also mit dem erweiterten Euklidischen Algorithmus lösen (Bestimmung von 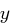 ).
).
Fall 2: Sei 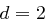 . Mit
. Mit 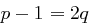 und
und 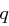 ungerade ergibt sich
ungerade ergibt sich 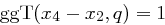 . Damit existiert das Inverse
. Damit existiert das Inverse 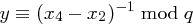 und es folgt
und es folgt
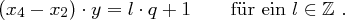
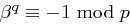 , da
, da 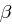 erzeugendes Element in
erzeugendes Element in 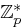 ist,
ist, 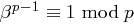 und die Gleichung
und die Gleichung 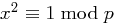 genau zwei Lösungen hat. Es ergibt sich:
genau zwei Lösungen hat. Es ergibt sich:
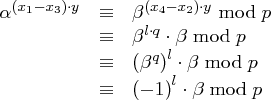
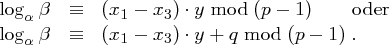
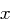 in
in 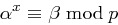 kann dann leicht die richtige Lösung ermittelt werden.
kann dann leicht die richtige Lösung ermittelt werden.
Fall 3: Sei 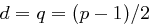 und damit
und damit 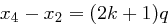 für ein
für ein 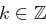 . Mit
. Mit 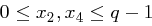 folgt aber
folgt aber 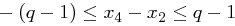 , also ist
, also ist 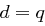 nicht möglich.
nicht möglich.
Fall 4: Für 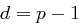 folgt
folgt 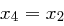 . Mit
. Mit 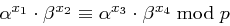 ergibt sich
ergibt sich 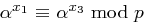 , also
, also 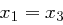 , da
, da 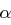 primitiv ist. Nach Annahme war jedoch
primitiv ist. Nach Annahme war jedoch 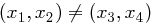 .
.