2. Suchen und Sortieren

2.1 Binäre Suche

Dieses Teilkapitel überschneidet sich stark mit dem aus der Vorlesung Theoretischen Informatik. Dennoch habe ich es hierhin kopiert, da ja nicht gararntiert ist, dass alle Teilnehmer und Teilnehmerinnen dieses Kurses auch in TI waren.

Erinnern Sie sich noch an das hier?

Ein Telefonbuch. Bildquelle: Wikimedia Commons

Vielleicht sind Sie ja dafür tatsächlich zu jung. Es ist ein Telefonbuch. Wenn man eine Telefonnummer herausfinden will, zum Beispiel vom Kfz-Mechaniker Windisch aus Freudenberg, dann schaut man im Telefonbuch unter "W" nach und blättert. Und heute? Da benutzt man immer noch ein Telefonbuch. Dies ist dann aber elektronisch, und das Blättern tun auch nicht Sie, sondern ein Rechner (oder viele). Sie können zum Beispiel Das Telefonbuch verwenden oder eine Suchmaschine Ihrer Wahl.

Und ob Sie eine Telefonnummer suchen oder etwas ganz Anderes, ein Großteil von dem, was Rechner erledigen müssen, beinhaltet, irgendwo Inhalte aus einer riesigen Datenmenge rauszufischen. Grund genug, diesem Thema ein paar Vorlesungsstunden zu widmen.

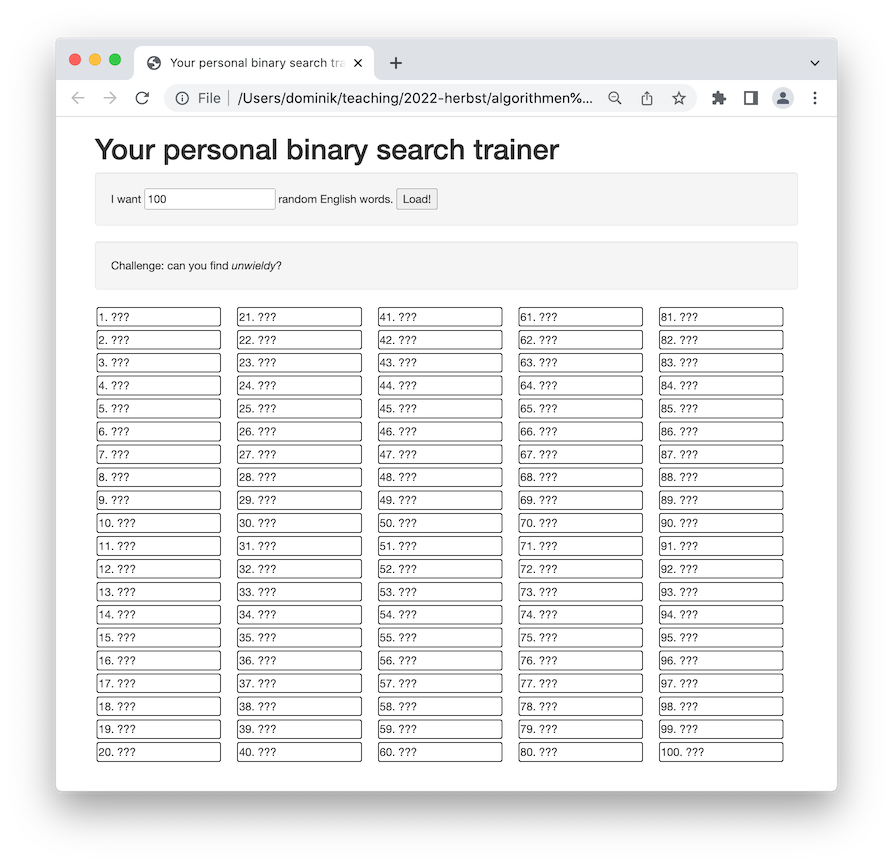
Um konkret zu werden: in der Datei englishVocabulary.txt finden Sie eine Liste von über 50.000 englischen Wörtern. Schauen Sie nach. Fällt Ihnen etwas auf? Die Wörter sind aphabetisch sortiert. Das sollte uns bei der Suche helfen. Spielen Sie das folgende Spiel, in dem Sie auf den Screenshot klicken:

Demo (binäre Suche)

Klicken Sie auf den Screenshot und spielen das Spiel.

Können Sie das gesuchte Wort mit höchstens sieben Klicks finden? Wahrscheinlich haben Sie rausgefunden, dass Sie als erstes irgendwo in der Mitte klicken sollten. Falls das dortige Wort "zu groß" ist, suchen Sie in der ersten Hälfte weiter; falls es zu klein ist, suchen Sie in der zweiten Hälfte weiter.

Abstraktion

Versuchen wir nun, die Aufgabenstellung und das Prinzip der binären Suche genauer zu verstehen. Wir haben ein Array $A$ der Größe $n$ gegeben. Es ist sortiert, es gilt also $A[0] \leq A[1] \leq \dots \leq A[n-1]$. Lassen Sie sich von dem mathematischen Symbol $\leq$ nicht täuschen. Es muss sich bei den Eleemnten $A[i]$ nicht um Zahlen handeln. Ganz generell kommen die Elemente aus einem Universum $\mathcal{U}$, auf dem eine lineare Ordnung definiert ist. Ohne jetzt definieren zu wollen, was das genau bedeutet, sei nur dies gesagt: die Elemente lassen sich vergleichen. In englishVocabulary.txt beispielsweise haben wir Strings gegeben, die wir alphabetisch (Mathematiker würden sagen: lexikographisch) vergleichen können.

Des Weiteren haben wir einen Suchwert $x$ gegeben. Ziel ist es, die Position $i$ mit $A[i] = x$ zu finden oder zu dem Schluss zu kommen, dass $x$ im Array $A$ nicht vorkommt. Hierfür führen wir zwei Indizes $l$ und $u$, welche für lower bound und upper bound stehen. Für diese gilt immer \begin{align} A[l] \leq x \lt A[u] \label{eqn-binary-search-invariant} \end{align} gilt. Wir wählen anfangs $l=-1$ und $u = n$, wobei wir die Konvention im Hinterkopf haben, dass $A[i] = -\infty$ für $i \lt 0$ und $A[i] = \infty$ für $i \geq n$.

Konvention: $A[-i] = -\infty$ für alle $i \lt -1$ und $A[i] = \infty$ für alle $i \geq n$. Insbesondere also $A[-1] = -\infty$ und $A[n] = \infty$.

Mit diesen "Randwerten" ist $A$ immer noch sortiert; allerdings müssen wir bei der Implementierung aufpassen, diese Array-Position nicht anzufassen. Die binäre Suche bildet nun das (abgerundete) arithmetische Mittel zwischen $l$ und $u$, nämlich $$ m := \floor {\frac{l + u}{2} } $$ und schaut nach, ob $A[m]$ kleiner oder größer als $x$ oder im Besten Fall gleich $x$ ist. Wenn $x \lt A[m]$ gilt, setzen wir $u := m$; wenn $ A[m] \leq x $ gilt, dann setzen wir $l := m$; in jedem Fall gilt $(\ref{eqn-binary-search-invariant})$ auch für die neuen Schranken $l$ und $u$. Wir wiederholen diesen Schritt, bis $u = l + 1$ gilt. In diesem Falle gilt entweder $A[l] = x$ und wir haben $x$ gefunden, oder aber \begin{equation} A[l] \lt x \lt A[l+1] \ , \end{equation} woraus wir schlussfolgern können, dass $x$ gar nicht in $A$ vorkommt. In der Praxis würden wir natürlich sofort abbrechen, wenn $A[m] = x$ gilt; für eine theoretische Worst-Case-Analyse spielt dies allerdings keine Rolle.

Algorithmus (Binäre Suche, Pseudocode)

Gegeben ein sortiertes Array $A[0..n-1]$ und einen Key $x$.

binarySearch(Array A, key x):                                
    l := -1, u := m 
    while u - l > 1: 
        m := (l+u)/2 
        if A[l] <= x then 
            l = m 
        else 
            u = m 
    return m

Die Funktion binarySearch(A,x) gibt den größten Index $j \in \Z$ zurück, für den $A[j] \leq x$ gilt.

Extremfälle. Falls $x$ kleiner ist als alle Elemente in $A$, dann gibt binarySearch den Wert $-1$ zurück. Dies ist ja korrekt, da per Konvention $A[-1] = -\infty$ gilt und somit $A[-1] = -\infty \lt x$. Falls $x$ größer als alle Elemente in $A$ ist, gibt binarySearch den Wert $n-1$ zurück. Falls $A$ ein leeres Array ist, also $n=0$ gilt, dann ist $x$ jedoch sowohl kleiner als auch größer als alle Elemente von $A$. Die Funktion binarySearch müsste laut unseren vorherigen Angaben also sowohl $-1$ als auch $n-1$ zurückgeben. Dies stellt glücklicherweise keinen Widerspruch dar, da ja in diesem Falle $-1 = n-1$ gilt. (Der letzte Absatz klingt vielleicht pedantisch; es lohnt sich allerdings, solche Extremfälle durchzudenken, gerade wenn Sie vorhaben, Ihre Algorithmen auch zu implementieren.)

Laufzeitanalyse. Wenden wir uns der Frage zu, wie viele Schritte die while-Schleife in binarySearch im schlimmsten Falle durchläuft, in Abhängigkeit von $n$. Betrachten wir hierfür den Wert $u-l$ und wie er sich im Verlauf der Ausführung verändert. Nach einem Schleifendurchlauf wird der Wert $u-l$ entweder zu $$ \floor {\frac{u+l}{2}} - l $$ oder $$ u - \floor {\frac{u+l}{2}} \ , $$ je nachdem, ob wir im linken oder rechten Teilintervall weitersuchen.

Behauptung. $\floor {\frac{u+l}{2}} - l = \floor{ \frac {u-l}{2}} $ und $ u - \floor {\frac{u+l}{2}} = \ceil { \frac{u-l}{2}}$.

Beweis. Falls $u-l$ eine gerade Zahl ist, dann ist $u+l$ auch eine gerade Zahl, und wir können in allen Gleichungen die Aufrundungs- bzw. Abrundungsstriche weglassen. In diesem Falle sind die beiden Gleichungen also korrekt.

Falls nun $u-l$ eine ungerade Zahl ist, dann ist $u+l$ auch ungerade; des Weiteren gilt für ungerade Zahlen $k$, dass $\floor{\frac{k}{2}} = \frac{k-1}{2}$ und $\ceil{\frac{k}{2}} = \frac{k+1}{2}$. Die erste behauptete Gleichung wird also zu

$$ \floor {\frac{u+l}{2}} - l = \frac{u+l-1}{2} - l = \frac{u-l-1}{2} = \floor{ \frac{u-l}{2}} \ , $$ wie behauptet. Die zweite Gleichung wird zu $$u - \floor {\frac{u+l}{2}} = u - \frac{u+l-1}{2} = \frac{u-l+1}{2} = \ceil {\frac{u-l}{2}} \ ,$$ und beide Gleichungen gelten. $\square$

Setzen wir $k := u-l$. Wir sehen also, dass anfangs $k=n+1$ gilt und in jedem Durchlauf $k$ durch höchstens $\ceil{\frac{k}{2}}$ ersetzt wird. Wir enden, wenn $k=1$ erreicht ist.

Wieviele Schritte braucht es, bis aus $k=n+1$ schlussendlich $k=1$ geworden ist? Machen wir es uns einfach und betrachten den Fall, dass $k$ immer gerade ist (bis auf $k=1$), also zum Beispiel $8 \rightarrow 4 \rightarrow 2 \rightarrow 1$. Für $n=8$ brauchen wir also (im Worst Case) drei Schleifendurchläufe. Für $n=32$ erhalten wir $32 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1$ und benötigen fünf Durchläufe. Unsere Beobachtung: wenn $n = 2^d$ gilt, die Länge unseres Arrays also eine Zweierpotenz ist, so wird binarySearch genau $d$ Schleifendurchläufe durchlaufen, also $\log_2(n)$ viele. Wenn nun $n$ etwas größer ist, also zum Beispiel $2^d + 1$, so durchläuft $k$ folgende Wertfolge: $$ 2^d + 1 \rightarrow 2^{d-1} + 1 \rightarrow \dots \rightarrow 9 \rightarrow 5 \rightarrow 3 \rightarrow 2 \rightarrow 1 $$ und wir benötigen insgesamt $d+1$ Durchläufe. Zusammenfassend: falls für den Startwert $k=n+1 \in \{2^{d-1}+1,\dots, 2^{d}\}$ gilt, so werden im Schlimmsten Fall $d$ Schleifendurchläufe benötigt. Kompakt lässt sich dies wie folgt formulieren:

Theorem Die Anzahl der Schleifendurchläufe von binarySearch auf einem Array aus $n$ Elementen ist im Worst Case $ \ceil{ \log_2 (n+1)}$.

Der genaue Ausdruck $ \ceil{ \log_2 (n+1)}$ ist schwierig zu merken. Allerdings wird es einfacher, wenn Sie sich folgende Beobachtung einprägen:

Beobachtung Die Binärdarstellung der Zahl $n$ besteht aus genau $ \ceil{ \log_2 (n+1)}$ Bits.

Also zum Beispiel $ (7)_2 = 111, (16)_2 = 1000$ und so weiter. Prägen Sie sich also zwei Dinge ein: (1) die binäre Suche auf einem Array mit $n$ Elementen braucht im schlimmsten Fall so viele Durchläufe, wie die Binärdarstellung der Zahl $n$ Bits hat; (2) dies ist ungefähr $\log_2(n)$.

Implementierung in Python

Schreiben wir nun eine kleine Funktion in Python, die binäre Suche implementiert.

def binarySearch (data, x):
    lower = -1
    upper = len(data)  
    while (upper - lower > 1):
        lookup = (upper + lower) // 2
        if (data[lookup] <= x):
            lower = lookup 
        else:
            upper = lookup 
        # end if 
    return lower

Python-Programme sind oft sehr kurz, weil Sie im Gegensatz zu Elm oder Java keine großen Typendeklarationen machen müssen und Fehlerbehandlung gänzlich ausblenden können. Daher eignet sich Python wunderbar, um Algorithmen quick and dirty zu implementieren. Verwenden Sie aber Python bitte nicht, um die Steuerungssoftware eines Atomkraftwerks zu schreiben!

Übungsaufgabe Kopieren Sie den Python-Code in eine Datei binarySearch.py und speichern Sie die Datei in einem sinnvollen Verzeichnis, beispielsweise home/AuK/code/binarySearch/. Speichern Sie auch englishVocabulary.py dort ab. Fügen Sie die folgende Zeile an den Anfang der Datei binarySearch.py ein:

from englishVocabulary import wordlist_sorted, wordlist_unsorted

Öffnen Sie eine Konsole und starten Sie das Python-Programm im Repl-Modus:

~/AuK/code/binarySearch $ python3 -i binarySearch      
binarySearch(wordlist_sorted, "yak")
57885
wordlist_sorted[57885]
'yak'

Geben Sie per Hand ein sortiertes Array ein, also beispielsweise data = [1,4,9,16,25] und spielen damit rum.

Testen Sie Grenzfälle wie Suchwörter, die kleiner sind als alle Einträge oder solche, die größer sind als alle. Was geschieht bei leeren Arrays?

Übungsaufgabe Schreiben Sie eine Funktion linearSearch, die das Array in linearer Suche durchgeht und dadurch auch auf unsortierten Arrays funktioniert.

Testen Sie sie auf der unsortierten Wortliste wordlist_unsorted, die ebenfalls englishVocabulary.py definiert ist.

Laufzeit mesen

Mit Python können Sie recht einfach die Laufzeit Ihrer Funktionen messen. Um das Ihnen noch leichter zu machen, habe ich ein kleines Modul timeMyPrograms.py geschrieben. Kopieren Sie die Datei in Ihren Verzeichnis .../code/binarySearch und fügen Sie oben in binarySearch.py die Code-Zeile

from timeMyPrograms import *

ein. Dann können Sie die Laufzeit wie folgt messen:

~/AuK/code/binarySearch $ python3 -i binarySearch
binarySearch(wordlist_sorted, "processor")
39136
measure_alg(binarySearch, wordlist_sorted, "processor")
1.2775002687703818e-05

Ganz allgemein können Sie mit measure_alg(alg, p_1, p_2, ..., p_n) die Laufzeit des Aufrufs von alg(p_1, p_2, ..., p_n) empirisch messen. Beachten Sie, dass die Zahl 1.2775002687703818e-05 die Floating-Point-Schreibweise ist für

\begin{align*} 1.2775002687703818 \times 10^{-5} \ . \end{align*} Die Laufzeit beträgt also eine gute hunderttausendstel Sekunde.

Übungsaufgabe Messen Sie empirisch die Laufzeit Ihrer Implementierungen von binarySearch und linearSearch. Um welchen Faktor unterscheiden sie sich?

Implizite binäre Suche

Binäre Suche taucht auch oft auf, ohne dass explizit ein Array vorliegt. Beispielsweise, wenn wir die ganzzahlige Wurzel einer Zahl berechnen wollen:

\begin{align*} {\rm intSqrt} : \mathbb{N} & \rightarrow \mathbb{N} \\ n & \mapsto \floor{\sqrt{n}} \end{align*}

Wir wollen hier explizit nicht auf die bereits vorhandene Bibliotheksfunktion math.sqrt zurückgreifen. Diese arbeitet insbesondere mit Floating-Point-Zahlen und liefert daher auch schnell falsche Ergebnisse:

~/AuK/code/binarySearch $ python3 -i binarySearch      
def sqrtInt(n): return math.floor(math.sqrt(n))                        
sqrtInt(16):
4
n = 3**40
sqrt(n*n) - n
-33 # Ouch!

Wir müssen es also selbst implementieren. Denken wir nach: ${\rm intSqrt}(n)$ ist die größte ganze Zahl $k$ mit $k^2 \leq n$. Daher der folgende Algorithmus:

def intSqrt(n):
    k = 0
    while (k*k <= n):
        k = k+1
    return k-1

Übungsaufgabe Experimentieren Sie mit der Funktion intSqrt. Wie weit kommen Sie mit vertretbarer Laufzeit? Was ist der Zusammenhang zwischen $n$ und der Laufzeit von intSqrt?

Was ist die Größe einer ganzen Zahl?

Die Laufzeit von intSqrt(n) ist ungefähr proportional zu der Anzahl der Schleifendurchläufe und somit zu $\sqrt{n}$ selbst. Das klingt jetzt gar nicht so schlecht. Nehmen wir aber als Beispiel einmal die Zahl $n := 2^{60}$. Offensichtlich ist $\sqrt{n} = 2^{30}$. Dies ist ungefähr eine Milliarde. Unser Algorithmus braucht also eine Milliarde Schleifendurchläufe. Auf einem schnellen Rechner und mit der C-Implementierung ginge das vermutlich in erträglicher Zeit über die Bühne. Ein zeitgenössisches Macbook (Stand Herbst 2023) mit einem Apple M2 Pro Prozessor hat 12 CPU-Kerne, von denen jeder bis zu 3,5 GHz hat. Seien wir unrealistisch optimitisch und nehmen an, ein Schleifendurchlauf von intSqrt bräuchte einen Prozessortakt, und darüberhinaus ist alles perfekt parallelisierbar (also auf die 12 CPU-Kerne) verteilbar, so dass das Macbook pro Sekunde $12 \cdot 3.5 \cdot 10^9 = $ 42 Milliarden Durchläufe schafft.

In diesem (unrealistisch optimistischen) Szenario würde intSqrt(2**80) also $\frac{\sqrt{2^{80}}{42 \cdot 10^9}} \approx 31$ Sekunden dauern. intSqrt(2**100) bereits tausendmal so lange, also fast einen halben Tag. Ist das gerechtfertigt? Ist 2**100 eine "große" Zahl? Fragen wir Python:

2**100                        
1267650600228229401496703205376

Das passt wunderbar auf eine Zeile. Gemessen an der Anzahl an Stellen, die wir brauchen, um diese Zahl zu repräsentieren, ist sie recht klein. Im Allgemeinen bemisst man die Größe einer Zahl (im Kontext von Algorithmen) als ihre Bitlänge, also die Anzahl der Bits in ihrer Binärdarstellung. Wie bereits weiter oben diskutiert hat die Zahl $n$ die Bitlänge

\begin{align*} \ceil{\log_2 (n+1)} \end{align*}

Anders herum gesagt: eine $k$-stellige Zahl $n$ (in Bits) ist mindestens $2^{k-1}$ und höchstens $2^{k - 1}$. Die Funktion intSqrt(n) benötigt also mindestens

\begin{align*} \sqrt{2^{k-1}} = 2^{\frac{k-1}{2}} \end{align*}

Schleifendurchläufe. Somit ist die Laufzeit exponentiell in der Bitlänge $k$. Intuitiver ausgedrückt: wenn wir die Bitlänge um 2 Bits erhöhen, dann verdoppelt sich die Laufzeit.

Quadratwurzel mit binärer Suche

Wenn wir ein Array mit den Quadratzahlen $A = [0, 1, 4, 9, 16, ..., m^2]$ gegeben haben, dann können wir für eine Eingabezahl $0 \leq n \leq k^2 $ per binärer Suche das größte $k$ lokalisieren, für das $A[k] \leq n$ gilt. Da $A[k] = k^2$, so gilt dann eben auch $k = {\rm sqrtInt} (n)$.

~/AuK/code/binarySearch $ python3 -i binarySearch.py                        
array = [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100]                        
binarySearch(array, 48)
6

Wir können also mittels binärer Suche die Quadratwurzel berechnen. Natürlich müssen (dürfen) wir das Array $A$ nicht explizit konstruieren (das würde zu viel Zeit und Platz beanspruchen). Wir müssen also eine implizite binäre Suche durchführen, in welcher der Array-Zugriff

        if (data[lookup] <= x):

durch einen Funktionsaufruf ersetzen.

Übungsaufgabe

Schreiben Sie in Python eine Funktion intSqrt (n), die die Funktion $$ n \mapsto \floor {\sqrt{n}} $$ berechnet. Ihre Funktion soll ohne Probleme die Quadratwurzel hundertstelliger Zahlen berechnen können.

Übungsaufgabe Messen Sie die Laufzeit Ihres Algorithmus mit measure_alg (intSqrt, 2**100), beispielsweise.

Legen Sie eine Tabelle an: wie entwickelt sich die empirisch gemessene Laufzeit mit der Bitlänge der Eingabezahl? Tip: Sie müssen schon sehr große Zahlen eingaben (tausendstellige, zehntausendstellige), um die Laufzeit zu "spüren".

Wenn Sie die Bitlänge verdoppeln, wie verändert sich die Laufzeit?

Untere Schranken

Übungsaufgabe

Ich habe Ihnen einen speziellen Algorithmus vorgestellt, der das gegenwärtige Suchareal in jedem Schritt halbiert. Ist dies optimal? Versuchen Sie zu beweisen, dass man im Schlimmsten Fall auch $ \ceil { \log_2 (n+1)}$ Schritte benötigt.

Formulieren Sie in Gedanken die binäre Suche als Spiel . Bob kennt das Array $A$. In jedem Schritt fragt Alice einen index $i$ an und Bob antwortet mit $A[i]$. Alice will möglichst schnell den Wert $x$ finden, und Bob will dies verzögern.
Tun Sie so, als wäre Bob ein adaptiver Gegner. Das heißt, er kann sich das Array $A$ Schritt für Schritt während des Spiels ausdenken. Er muss aber immer konsistent antworten, d.h. wenn Alice sowohl die Indizes $i \lt j$ angefragt hat, müssen Bobs Antworten die Bedingung $A[i] \lt A[j]$ erfüllen.
Zeigen Sie, dass Sie den adaptiven Bob durch einen nicht-adaptiven Bob ersetzen können (also durch ein Array $A$, dass von vornherein feststeht), so dass Alice dennoch nicht schneller zum Ziel kommt (hier ist es wichtig, dass Alice deterministisch ist, also keinen Zufall verwenden darf).