2. Suchen und Sortieren

2.3 Mergesort

Jetzt lernen wir den ersten "effizienten" Algorithmus kennen: Mergesort. Dieser Algorithmus teilt array in zwei gleich große Hälften array1 und array2, sortiert diese (rekursiv, durch einen Aufruf von Mergesort selbst), und verschmilzt die beiden sortieren Teil-Arrays mit Hilfe einer Subroutine merge zu einer großen sortieren Gesamtliste.

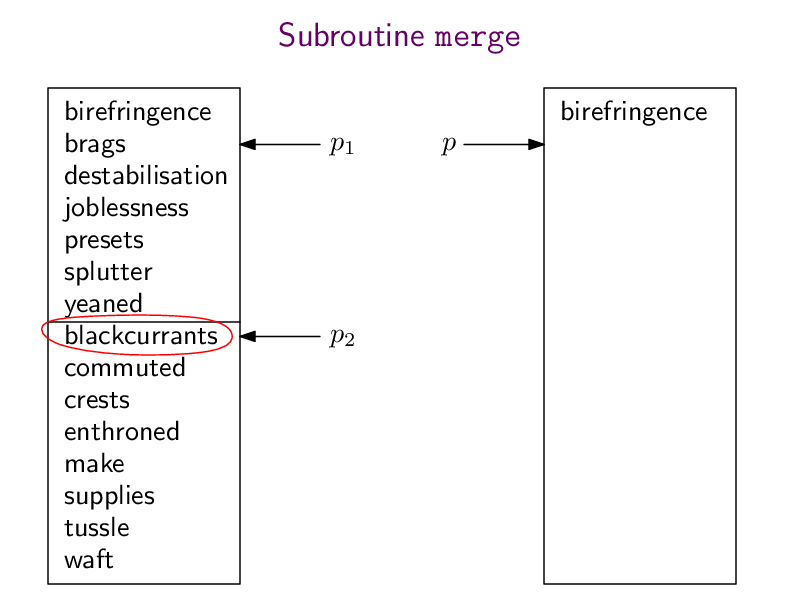
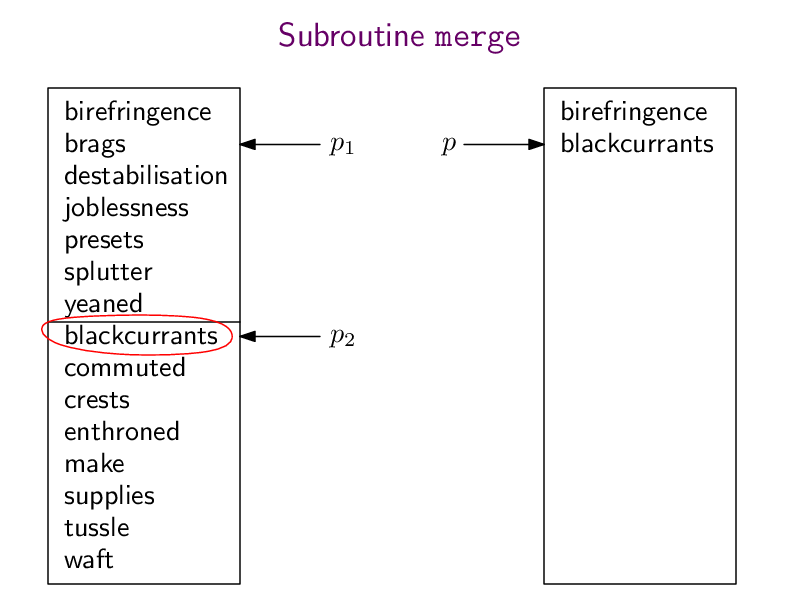
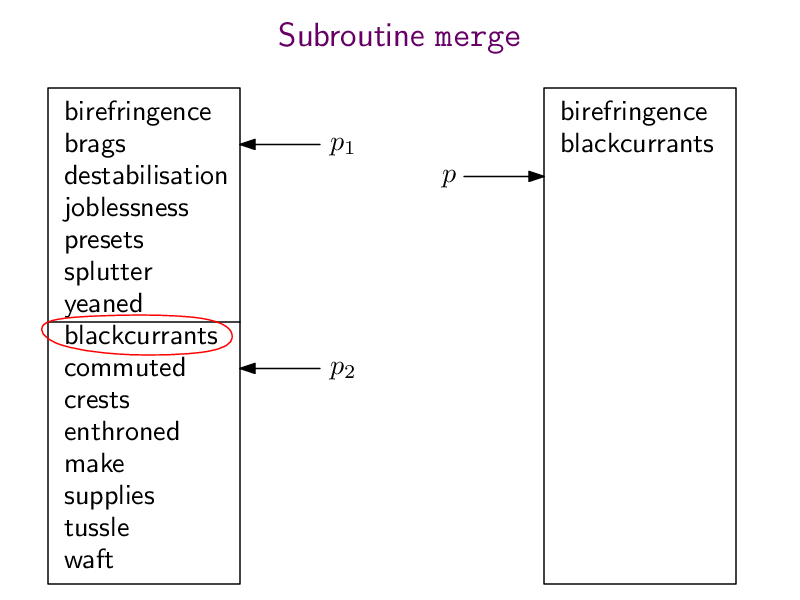
Hier wieder die pdf-Datei mergeSort.pdf mit der ganzen Animation und hier meine Python-Implementierung:

def merge (array1, array2):
    n1 = len(array1)
    n2 = len(array2)
    n = n1 + n2
    result = [0] * n
    p = 0 # pointer to where to insert the next element into result
    p1 = 0 # pointer to where to read the next element of array1
    p2 = 0 # pointer to where to read the next element of array2

    while (p < n):
        if (p2 == n2 or (p1 < n1 and array1[p1] < array2[p2])):
            result[p] = array1[p1]
            p1 = p1+1
        else:
            result[p] = array2[p2]
            p2 = p2+1
        p = p+1
    return result

def mergesort(array):
    if (len(array) < 2):
        return array
    middle = len(array) // 2
    array1 = array[0:middle]
    array2 = array[middle:]
    array1 = mergesort(array1)
    array2 = mergesort(array2)
    return merge(array1, array2)                    
                

Bevor wir die Laufzeit analysiere, sollten wir den Algorithmus experimentell testen. Hierzu brauchen wir wieder folgende Dateien:

• Kopieren Sie den obigen Code in eine Datei mergeSort.py. In den gleichen Ordner wie diese kopieren Sie bitte
• timeMyPrograms.py und
• englishVocabulary.py, falls diese noch nicht in dem Ordner sein sollten.

python3 -i mergeSort.py
measure_alg (selectionSort, wordlist_unsorted)
210.4567011850013 # Laufzeit in Sekunden
measure_alg (insertionSort, wordlist_unsorted)
343.31445141899894 # überraschend, dass es länger dauert
measure_alg (mergesort, wordlist_unsorted)
0.3041463459994702
                

Der Unterschied zwischen den langsamen Algorithmen SelectionSort und InsertionSort und dem schnellen Mergesort ist gigantisch: Mergesort ist über tausendmal schneller als Insertion-Sort und knapp 700 mal schneller als SelectionSort. Dabei gibt es mehrere Dinge, die oberflächlich gegen Mergesort sprechen:

• Mergesort ist rekursiv. Es wird also Overhead für das Stack-Management geben.
• Mergesort ist nicht in-place: wir vergeben in Zeile 5 von Mergesort neuen Speicherplatz, während Insertion-Sort und Selection-Sort rein auf dem gegebenen Platz von array arbeiten.

Was Sie hier sehen, ist nicht clevere Implementierung. Was Sie sehen, ist ein überlegener Algorithmus.

Suboptimale Laufzeitanalyse

Wie können wir von hier aus die maximale Anzahl von Vergleichsoperationen in einem Aufruf von mergeSort(array) bestimmen? Da MergeSort ein rekursiver Algorithmus ist, bietet es sich immer an, seinen Rekursionsbaum zu skizzieren. Für ein Array der Größe 14 sähe der zum Beispiel so aus:

Jedes graue Rechteck stellt einen Aufruf von mergesort dar, und die Zahl darin ist die Größe des Arrays bei diesem Aufruf. Wie wir in Lemma 1.2 gesehen haben, ist die Zahl in dem grauen Rechteck auch eine obere Schranke für die Anzahl der Vergleiche, die merge macht, um die zwei Teilarrays wieder zu einem großen zusammenzufügen. Daher:

Gibt es eine einfache Formel für diese Summe? In der Tat:

Sehen Sie: jede "Ebene" des Baumes bis auf die letzte ergibt in Summe 14, also im Allgemeinen \(n\), die Größe des Eingabearrays. Um uns das Leben einfacher zu machen, runden wir großzügig auf und sagen: jede Ebene summiert sich zu höchsetns \(n\) auf. Daher gilt: die Anzahl der Vergleiche ist \(n\) mal die Anzahl der Ebenen im Baum. Der Rekursionsbaum hat genau

\begin{align*} \ceil {1 + \log n } \end{align*}

Ebenen. Daher schließen wir nun:

Optimale Analyse

Wir beginnen mit einer verbesserten Version von Lemma 1.2:

Mit diesem frischen Wissen betrachten wir noch einmal den Rekursionsbaum:

Wie zuvor ist die schwarze Zahl im Rechteck die Größe des Teilarrays; die rote daneben ist eins weniger und stellt eine obere Schranke für die Vergleichsoperationen dar, die merge an diesem Knoten ausführt. Im weiteren sei \(d\) die Höhe des Baumes, also der größte Abstand von einem Blatt zur Wurzel; in anderen Worten: die Anzahl der Ebenen minus 1. Wir numerieren die Ebenen mit 0 beginnend, also \(0, 1, 2, \dots, d\). Sammeln wir ein paar Fakten:

1. \(d = \ceil{\log n }\).
2. Ebene \(d\), also die unterste, hat nur rote Nullen, erzeugt also keine Vergleichsoperationen. Das sehen wir auch im Pseudocode, weil dann nämlich die Bedingung len(array) < 2 erfüllt ist und Zeile 22 ausgeführt wird.
3. Die Ebenen \(0, 1, 2, \dots, d-1\) haben \(1, 2, 4, \dots, 2^{d-1}\) Knoten. Ganz allgemein: Ebene \(i\) hat \(2^i\) Knoten, solange \(0 \leq i \leq d-1\) ist.

Wir können von nun an Ebene \(d\) ignorieren. Die Sume der schwarzen Zahlen in den Ebenen 0 bis \(d-1\) ist \(nd\). Die der roten Zahlen ist \(nd\) minus die Anzahl der Knoten in den Ebenen \(0\) bis \(d-1\).

\begin{align*} \textnormal{Anzahl der Knoten in den Ebenen } 0, \dots, d-1 = 1 + 2 + 4 + \cdots + 2^{d-1} = 2^d - 1\ . \end{align*} Und somit ist die Gesamtzahl der Vergleichsoperationen maximal \(nd - 2^d + 1\).

Die Schranke von \(n-1\) Vergleichsoperationen für merge ist eine obere Schranke. Für manche Arrays kann es schneller gehen. Um nun zu zeigen, dass auch unsere Analyse von mergeSort optimal ist, müssen wir ein Array der Länge \(n\) konstruieren, so dass jeder Aufruf von merge im Rekursionsbaum die maximal mögliche Anzahl von Vergleichsoperationen nach sich zieht. Jedes Teilarray muss also auch wieder "so schlimm wie möglich" aussehen.