4.3 Binäre Suchbäume

In vielen Fällen wollen wir nicht nur am Anfang oder Ende unserer Datenstruktur etwas schreiben, sondern an beliebigen Stellen. Ganz allgemein wünschen wir uns eine Datenstruktur, die folgende Operationen unterstützt:

find <key>           // findet das Paar (key,value) und gibt value zurück (oder null, wenn nicht vorhanden)
insert <key> <value> // fügt das Paar (key,value) ein und löscht ein etwaiges älteres Paar (key, oldValue) 
delete <key>         // löscht das Paar (key,value), sofern vorhanden

Wir wollen also Key-Value-Paare speichern, ähnlich wie in der Liste german-words.txt. Eine solche Datenstruktur nennt man im Allgemeinen ein Dictionary. Die meisten Programmiersprachen bieten Dictionarys bereits in der ein oder anderen Form an. Hier setzen wir uns mit den Möglichkeiten auseinander, ein solches zu implementieren und untersuchen jeweils, wie schnell (oder langsam) die jeweiligen Operationen sind.

Als Stack, also z.B. verkettete Liste.
- find <key>: wir müssen, wenn wir Pech haben, die ganze Liste durchlaufen; $O(n)$.
- insert <key> <value>: wir legen das Paar einfach auf den Stack drauf; das braucht $O(1)$ Zeit; wenn wir allerdings vermeiden wollen, dass es mehrere Einträge mit dem gleichen Key gibt, dann müssen wir die ganze Liste durchlaufen: $O(n)$.
- delete <key>: gleich wie find
Als Array, das immer nach den Werten der Schlüssel sortiert ist (z.B. alphabetisch, aufsteigend).
- find <key>: Wir wenden binäre Suche an: $O(\log n)$.
- insert <key> <value>: Wir können den Einfügeort mittels binärer Suche schnell finden, müssen dann aber alles, was danach kommt, um eins nach rechts verschieben: $O(n)$.
- delete <key>: gleiches wie find; wir können zwar mittels binärer Suche die Stelle finden, müssen aber alles, was rechts davon steht, um eins nach links verschieben.

Um alle drei Operationen insert, find, delete in schneller (hier: $O(\log n)$) Laufzeit zu implementieren, brauchen wir eine neue Datenstruktur. Als erstes stellen wir den Binärbaum vor. Ein Binärbaum ist eine rekursive Datenstruktur, die entweder

ein leerer Baum ist, bestehend aus einem Blatt, oder
ein innerer Knoten mit einem Datenelement (beispielsweies einem String) und einem linken Kind und einem rechten Kind, die wiederum Binärbäume sind.

Den obersten Knoten nennen wir die Wurzel. Es ist recht problemlos, Binärbäume als Datentypen in Java oder Elm zu definieren.

public class BST {
    public String data;
    public BST leftChild;
    public BST rightChild;
    public BST (String data, BST left, BST right) {
        this.data = data;
        leftChild = left;
        rightChild = right; 
    }
}

module BST exposing (..)


type BST
    = Leaf
    | Node String BST BST

Den folgenden Baum:

können wir dann wie folgt erzeugen:

// in Java
BST tree = new BST("z", new BST("e", null, new BST ("a", null, null)), null);

-- in Elm                                    
tree: BST 
tree = Node "z" (Node "e" Leaf (Node "a" Leaf Leaf)) Leaf

Binäre Suchbäume (Binary Search Trees, BST)

Ein Binärbaum ist ein Binärer Suchbaum (Abkürzung BST), wenn die in den inneren Knoten gespeicherten Elemente geordnet sind; konkret: wenn ein innerer Knoten das Element $x$ hat, dann sind alle Elemente im linken Teilbaum kleiner als $x$ und alle Elemente im rechten Teilbaum größer als $x$. Wir sprechen nun auch nicht mehr von Elementen, sondern von Schlüsseln / Keys. Hier sehen Sie ein Beispiel, in welchem nacheinander Schlüssel in einen anfangs leeren BST eingefügt werden:

Klicken Sie auf das folgende Bild, um zu meiner interaktiven BST-App zu gelangen. Hier können Sie mit insert, find, delete experimentieren.

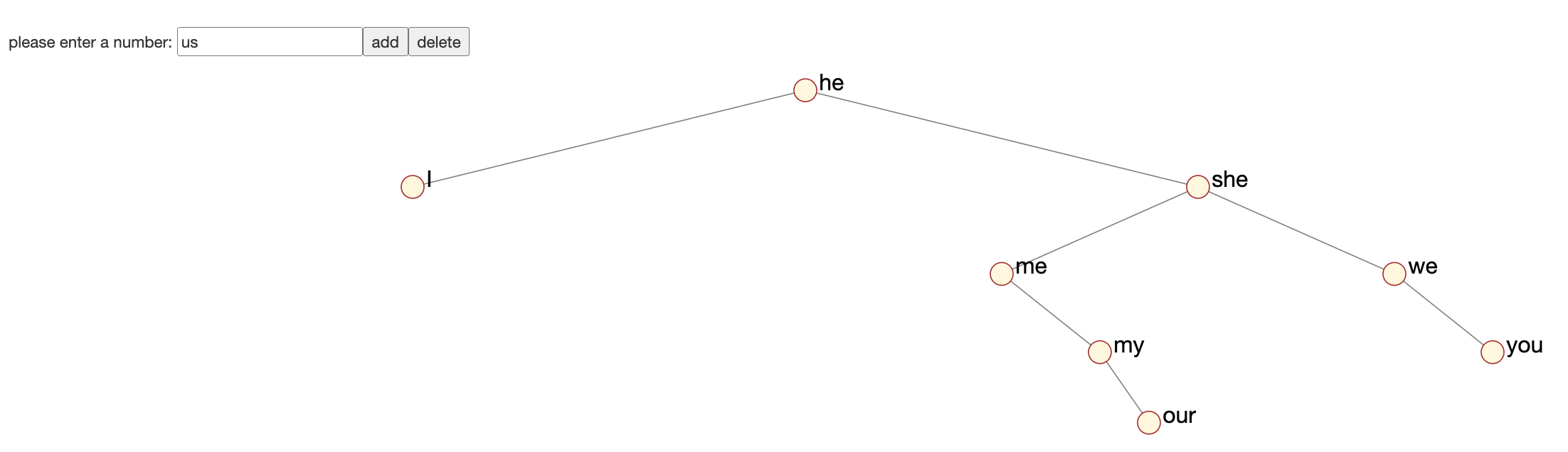
Hier finden Sie meine Java-Implementierung für binäre Suchbäume: BT.java

Im folgenden werden wir BSTs formal definieren und Methoden zum Suchen, Einfügen und Löschen finden.

Definition

Ein binärer Suchbaum, kurz BST (vom Englischen binary search tree) ist wie folgt rekursiv definiert: es ist entweder ein leerer Baum, den wir mit $\box$ bezeichnen, oder er ist nichtleer und von der Form

wobei in diesem Falle

wir $x$ als den Key des Wurzelknotens bezeichnen,
$L$ und $R$ wiederum BSTs sind,
alle Keys in $L$ kleiner als $x$ sind,
alle Keys in $R$ größer als $x$ sind.

Beachten Sie, dass wir im obigen Beispiel mit of, to, in... die leeren BSTs nicht gezeichnet haben. Mit den leeren BSTs müsste das Endergebnis des oberen Baums dann so aussehen:

Der (Pseudo-) Code für Suchen (find) und Einfügen (insert) in einem BST schreibt sich fast von selbst:

Der Code für das Einfügen ist nur leicht komplizierter:

Löschen ist etwas schwieriger. Ich teile es auf in delete, was erst einmal den Key überhaupt sucht und dann deleteRoot aufruft, was den Wurzelknoten mitsamt Key löscht.

Für delRoot müssen wir uns was überlegen. Einfach ist es, wenn der linke Teilbaum leer ist; dann ergibt delRoot(T) einfach den rechten Teilbaum. Ganz analog, wenn der rechte Teilbaum leer ist:

Wenn aber weder der linke noch der rechte Teilbaum leer ist, was dann? Eine Idee wäre, im rechten Teilbaum $R$ das kleinste Element zu finden; dieses sitzt in einem Blatt von $R$, und zwar ganz links; dann schreiben wir dieses Element in den Wurzelknoten und löschen das entsprechende Blatt von $R$.

Ich hatte fehlerhaft angenommen, dass das Minimum von $R$ in einem Blatt wohnt. Das muss nicht der Fall sein. Wie also können wir es löschen? Brauchen wir hierfür Rekursion oder geht es einfacher?

Übungsaufgabe Schreiben Sie Pseudo-Code für findMin und deleteMin.

Übungsaufgabe Machen Sie in dem obigen Beispiel weiter und fügen Sie he, by, or, on, do, if, me ein.

Übungsaufgabe Nehmen Sie den obigen Suchbaum und löschen Sie of.

Ganz allgemein finden wir BSTs gut, wenn Sie geringe Höhe haben. Die Höhe eines Baumes ist der Abstand von der Wurzel zu dem am weitesten entfernten Blatt. Wir schreiben $\height(T)$. Für ein Array $[a_1, a_2, \dots, a_n]$ schreiben wir ${\rm BST}([a_1, a_2, \dots, a_n])$ für den BST, der entsteht, wenn wir die Elemente des Arrays in dieser Reihenfolge einfügen. Zum Beispiel:

und damit $\height({\rm BST}([1,2,3])) = 2$ und $\height({\rm BST}([2,1,3])) = 1$.

Übungsaufgabe Stellen Sie sich vor, Sie fügen die Elemente $a_1, a_2, \dots, a_n$ in einen anfangs leeren BST ein. Nennen wir diesen Baum ${\rm BST}([a_1, a_2, \dots, a_n])$. Jetzt fügen Sie ein weiteres Element $a_{n+1}$ ein. Offensichtlich kann die Höhe des Baumes nicht abnehmen, also $$ \height(\BST(\array)) < \height([{\rm BST}](\array + [{\rm new\_element}])) $$ Wenn wir aber das Array ändern und am Anfang ein Element einfügen, dann kann dies tatsächlich die Höhe verringern:

Finden Sie ein Array $[a_0, a_1, a_2, \dots, a_n]$, so dass $$ \height(\BST([a_0, a_1, a_2, \dots, a_n])) < \height(\BST([a_1, a_2, \dots, a_n])) $$ gilt.

Tip. Meine Beispiel-Arrays haben Größe 4 bzw. 5. Ich habe also ein Array der Länge 5, welches mir einen Baum der Höhe 2 gibt; wenn allerdings das erste Element im Array nicht da wäre, würde das restliche Array (der Länge 4) mir einen Baum der Höhe 3 (also schlechter) geben.

Übungsaufgabe Wiederholen Sie die vorherige Aufgabe aber versuchen Sie, ein extremeres Ergebnis zu erreichen. Ich habe beispielsweise ein Array array gefunden, für das gilt $$ \height(\BST(\array)) > 2 \cdot \height(\BST([a_0] + \array)) - 2 \ . $$ In Worten, wenn Sie das erste Element $a_0$ wegnehmen, dann verdoppelt sich die Höhe des Baumes ungefähr. Finden Sie so ein Beispiel.

Übungsaufgabe Im Geiste der vorherigen beiden Aufgaben, zeigen Sie, dass das Wegnehmen des Elements $a_0$ am Anfang des Arrays die Höhe des resultierenden BSTs nicht mehr als verdoppeln kann, also $$ \height(\BST(\array)) < 2 \cdot \height(\BST( [a_0] + \array)) $$ Hinweis. Das ist nicht ganz einfach. Ich empfehle Ihnen, Ihr Array als $[p, a_1, a_2, \dots, a_n]$ zu schreiben und dann mit $[b_1,\dots,b_k]$ die Elemente zu bezeichnen, die kleiner als $p$ sind (in der Reihenfolge, in der sie in $\array$ vorkommen), und mit $c_1,\dots,c_{n-k}$ diejenigen, die größer als $p$ sind. Vergleichen Sie dann $\height(\BST([b_1,\dots,b_k]))$ mit $\height(\BST([a_1,\dots,a_n]))$.

Beobachtung Die Laufzeitkomplexität für find, insert, delete in einen BST ist begrenzt durch die Höhe des Baumes, also die Länge des längsten Pfades von der Wurzel zu einem Blatt.

Übungsaufgabe Finden Sie eine "schlechte" Sequenz von $n$ insert-Operationen, die insgesamt quadratisch viele Schritte verursacht, also $\Theta(n^2)$ viele.

Die Herausforderung ist nun, die Implementierung von Binärbäumen so anzupassen, dass keine degenerierten Bäume entstehen, dass also idealerweise die Höhe des Baumes möglichst klein ist. Wie klein kann sie überhaupt sein? Wenn ein Baum Höhe $d$ hat, also die Länge eines Pfades von Wurzel zu einem Blatt höchstens $d$ Kanten hat, dann können wir die Knoten des Baumes in Level $0,1,2,\dots,d$ einteilen, wobei der Wurzel in Level 0 sitzt. Da jeder Knoten maximal zwei Kinder hat, gibt es in Level $i$ maximal $2^i$ Knoten. In Level $d$ gibt es nur noch Blätter. Also gibt es maximal $$ 1 + 2 + 4 + 8 + \cdots + 2^{d-1} = 2^d-1 $$ innere Knoten, und somit ist $n$, die Anzahl der gespeicherten Schlüssel-Wert-Paare, höchstens $$ n \leq 2^d - 1 \ . $$ Wir lösen diese Ungleichung nach $n$ auf und erhalten

Beobachtung. Sei $T$ ein BST mit $n$ inneren Knoten, also $n$ Schlüssel-Wert-Paaren. Dann gilt $$ \height(T) \geq \log_2(n+1) \ . $$

Soweit die untere Schranke. Dieses Optimum von $\log_2(n+1)$ wird im Ernstfall nicht realistisch sein, aber vielleicht $2 \log(n+1)$ oder Ähnliches, können wir also $O(\log n)$ erreichen? Ich werde im folgenden drei Methoden vorstellen, wie wir Tiefe $O(\log n)$ erreichen können. Für alle sind insert und delete deutlich komplexer als für "naive" BSTs.

Treaps. Wir haben bereits gesehen, dass BSTs besonders schlecht werden, wenn die Elemente in geordneter Reihenfolge eingefügt werden. Was, wenn die Reihenfolge zufällig ist? Treaps simulieren eine zufällige Einfüge-Reihenfolge, indem sie jedem Schlüssel-Wert-Paar ein Gewicht zuordnen. "Leichte" Elemente sollen dann im BST höher stehen als "schwere". Dies garantiert, dass der BST immer so aussieht, als hätten wir die Elemente von leicht nach schwer sortiert eingefügt. Wenn wir schließlich die Gewichte zufällig wählen, sieht der BST so aus, als hätten wir die Elemente in zufälliger Reihenfolge eingefügt.
Vorteil. Treaps sind recht einfach zu implementieren; wir müssen nur pro Element zusätzlich ein Gewicht speichern.

Nachteil. Treaps sind randomisiert; alle oberen Schranken gelten also nur im Erwartungswert. Das heißt, Sie können rein theoretisch Pech haben und mit einem degenerierten Baum und hohen Suchzeiten enden. Die Laufzeitanalyse ist moderat kompliziert (wenn Sie keine Erfahrung mit Wahrscheinlichkeitsrechnung haben).
B-Bäume. Der Idealfall eines BSTs ist ja, dass er perfekt balanciert ist, also alle Blätter gleichen Abstand von der Wurzel haben. Das geht aber selbst theoretisch nur dann, wenn die Anzahl der Elemente die Form $n = 2^d-1$ hat. Die Idee der B-Bäume ist, dass wir die Bedingung jeder innere Knoten hat genau zwei Kinder aufweichen in jeder innere Knoten hat zwei oder drei Kinder. Diese flexiblere Struktur erlaubt uns, jederzeit alle Blätter auf gleichem Niveau zu halten und somit immer eine perfekt balancierte Struktur zu unterhalten.
Vorteil. Die Laufzeitanalyse ist extrem einfach. Die Höhe ist immer maximal $O(\log n)$.
Nachteil. Die Implementierung ist etwas komplizierter.
Rot-Schwarz-Bäume (Red-Black-Trees). Dies sind wiederum "richtige" BSTs, in denen jeder innere Knoten genau zwei Kinder hat. Jeder innere Knoten bekommt eine Farbe Schwarz oder Rot, die gewissen Regeln unterworfen sind. Diese Regeln helfen uns, sicherzustellen, dass die Höhe des Baumes immer $O(\log n)$ ist.
Vorteil. Rot-Schwarz-Bäume sind BSTs, und dadurch ist der Code für find genau der Gleiche wie für naive BSTs. Die Laufzeitanalyse ist offensichtlich.

Nachteil. Die Regeln für insert und delete müssen mehrere verschiedene Fälle von Knotenfärbungen beachten; das erschwert die Implementierung und auch das Verständnis.

Beachten Sie, dass in der Praxis weitere Vor- und Nachteile dazukommen können, die von Anwendungsfall zu Anwedungsfall variieren. Schwierigkeit der Laufzeitanalyse und Schwierigkeit der Implementierung sind für die Praxis auch nicht wirklich von Relevanz, da Sie ja meistens auf Implementierungen zurückgreifen können.