5.8 Programmierprojekt: Schildkrötenzeichner
Organisatorisches
Abgabetermin: Montag, 3. Juli 2023
Aufgaben: Die in diesem Teilkapitel als Testataufgabe gekennzeichneten Aufgaben.
Format: Kompilierfähige Elm-Quelldatei. Ich werde bei jeder Testataufgabe darauf extra eingehen.
Material: Die elm-Dateien, die wir bereits in der Veranstaltung geschrieben haben oder die Sie als Hilfsdateien brauchen werden, finden Sie gezippt in elm-project-sources-for-students.zip. Ihr Code soll/darf auf diesem aufbauen.
Fragen und Probleme: Wenn Sie an einer Stelle nicht weiterkommen, kontaktieren Sie mich einfach.
Das Projekt
Ziel dieses Programmierprojektes ist es, eine kleine Zeichenrobotersprache zu entwerfen. Wir
folgen hier
recht genau dem in Christian Wagenknechts und Michael Hielschers Buch Formale Sprachen,
abstrakte Automaten und Compiler,
allerdings wird unsere Implementierung anders sein.
Bei der Zeichensprache handelt es sich um eine Turtle Graphics, eine
Schildkrötengrafik. Die "Schildkröte" ist ein imaginärer Cursor, den Sie mit den Befehlen
move und rotate
steuern können. Zusätzlich können Sie mit pen eine Farbe wählen.
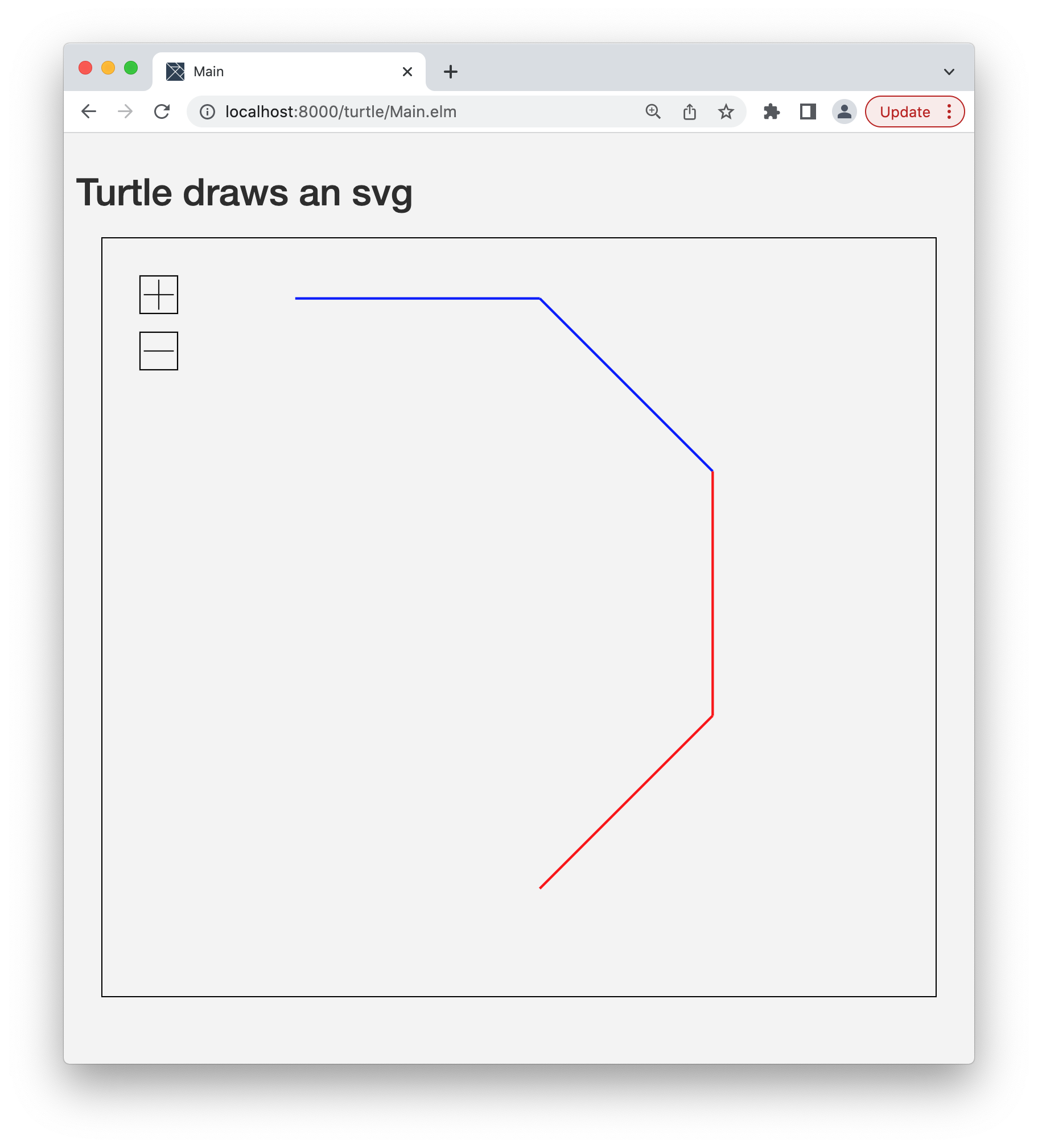
würde beispielsweise folgendes Bild erzeugen:pen blue;move 100;rotate 45;move 100;rotate 45;pen red;move 100;rotate 45;
Unsere Sprache soll auch repeat-Befehle zulassen: mit repeat n [ P ]
wird das Programm P
wiederholt, und zwar P in der Position und Richtung,
die sie am Ende der ersten Ausführung erreicht hat.
width 0.1;repeat 20 [jump 200;turn 20;repeat 100 [move 300;turn 170;]]
erzeugt dann beispielsweise das folgende, deutlich komplexere Bild:

Ziel ist es, eine Web-Anwendung zu schreiben, in der die User links ein Turtle-Programm eingeben können und die dann das Programm in eine Zeichnung übersetzt. Den Code, der gewisse Elm-Objekte dann konkret als Svg-Grafik zeichnet (wie in den Screenshots) werde ich Ihnen zur Verfügung stellen. Wir werden dieses Ziel in mehrere kleine Schritte zerlegen.
- Lexing. Der Eingabe-String soll in logische Bausteine (Tokens) zerlegt werden,
wobei auch schon der Whitespace eliminiert wird.
Beispielsweise:
Dies können Sie mit einem Mealy-Automaten ähnlich zum letzten Programmprojekt erledigen.Turtle.lex "pen green; repeat 10 [move 5; rotate 45;]"[Command "pen", Value "green", Semic, Command "repeat", Value "10", Open, Command "move", Value "5", Semic, Command "rotate", Value "45", Semic, Close] : List TurtleToken -
Parsing. Hierfür brauchen wir eine kontextfreie Grammatik, die die obigen Tokens als
Terminalsymbole nimmt.
"pen"ist also ein Terminalsymbol unserer Grammatik. Eine Regel wäre beispielsweise -
Den Parse-Tree (also Ableitungsbaum) in eine sinnvolle Datenstruktur übersetzen,
beispielsweise
type TurtleCommand = Pen String | Rotate Float | Move Float | Repeat Int (List TurtleCommand) -
Ein Elm-Programm schreiben, dass eine
List TurtleCommanddann konkret zeichnet. Hierfür werde ich Ihnen einen Großteil des Codes zur Verfügung stellen. Alternativ: eine Funktion, die eineList TurtleCommandin einen String umwandelt, der die Zeichnung im svg-Format beschreibt, sodass Sie dann die Zeichnung als svg-Datei abspeichern können.
Wir werden uns nun jeden einzelnen Schritt genauer ansehen.
1. Lexing
TurtleLexer.elm, die einen
Typ TurtleToken oder ähnlich definiert und einen Mealy-Automaten implementiert,
welcher
den Programm-String wie oben exemplarisch illustriert in solche Tokens zerlegt:
Turtle.lex "pen green; repeat 10 [move 5; rotate 45;]"[Command "pen", Value "green", Semic, Command "repeat", Value "10", Open, Command "move", Value "5", Semic, Command "rotate", Value "45", Semic, Close] : List TurtleToken
Abgabeformat: eine Datei TurtleLexer.elm, die eine Funktion
parse: String -> List TurtleToken oder ähnliches implementiert und
mehrere Beispielstrings definiert, anhand derer die Funktion parse getestet
werden kann.
2. Parsing.
Hier definieren Sie eine kontextfreie Grammatik, deren Terminalsymbole die Tokens der letzten
Aufgabe sind,
und die die Struktur der Turtle-Programme (insbesondere die Verschachtelung mit den
repeat-Befehlen)
beschreibt.
repeat n [ Block ] innerhalb von
Block wieder
repeat-Befehle auftauchen können. Eine Subtilität ist hier, dass die
Terminalsymbole
die TurtleTokens sind. In der Produktion
Command -> pen color;ist
color ein Terminalsymbol.
Wenn Sie sich unsicher sind, was erlaubt sein soll und was nicht, fragen Sie mich einfach!
Abgabeformat: eine Textdatei, in der Sie die Grammatik definieren.
Abgabeformat: ein Bild mit der Zeichnung des Automaten.
Char sind sondern irgendwelche Tokens, könnte die Signatur so aussehen:
turtleGrammar : ContextFreeGrammar TurtleToken TurtleNonterminal ... turtleDKautomaton : DKAutomaton TurtleToken TurtleNonterminal TurtleDKstate
Der Kernpunkt ist nun, dass die Transition, die der Automat bei Eingabe des Tokens
Value "red" macht, unabhängig davon ist, ob da jetzt red oder
blue oder was auch sonst was steht; das sind ja alles Inkarnationen der
gleichen "Terminalsymbol-Vorlage". In Elm können Sie das einfach mit Pattern Matching
erledigen:
delta : State -> Symbol TurtleToken TurtleNonterminal -> State =
delta state symbol =
case (state, symbol) of
(bla, Command "move") ->
Ihr Code hier
(bla, Value s) ->
Hier lasen Sie offen, ob jetzt Value "red" oder Value "10" oder sonst was steht
...
und schon kann Ihr DK-Automat eine unendliche Menge von Terminalsymbolen verkraften, weil diese eben per Pattern Matching zu endlich vielen Fällen zusammengefasst werden.
Abgabeformat: eine Datei TurtleGrammar.elm.
Jetzt sollten Sie eigentlich Ihre Datei
TurtleGrammar.elm
in meine Datei
importieren
und sich die Parse-Bäume anschauen:
-- import Tgrammar as Grammarimport TurtleGrammar as Grammar
3. Vom Parsebaum zum Turtle-Programm
Wir haben nun einen Parsebaum, dessen Knoten mit Nichtterminalen wie beispielsweise
ProgramLine oder Program beschriftet ist und dessen Blätter
Terminalsymbole wie Command "move" oder Value "100" sind.
Wir müssen das nun in eine problemspezifische Datenstruktur übersetzen.
TurtleProgram.elm an, in welcher
Sie folgenden Datentypen definieren:
type TurtleCommand
= Pen String
| Rotate Float
| Move Float
| Repeat Int (List TurtleCommand)
type alias TurtleProgram : List TurtleCommand
Abgabeformat: die Datei TurtleProgram.elm.
parseTreeToTurtleProgram: ParseTree TurtleToken TurtleNonterminal -> TurtleProgramwelches einen Parsebaum in ein Objekt vom Typ TurtleProgram umwandelt.
Hierfür müssen Sie rekursiv durch den Parsebaum gehen und schauen, um welches
Nichtterminal es sich am aktuellen Knoten handelt und den dann entsprechend
übersetzen.
Abgabeformat: die Datei TurtleGrammar.elm, die nun eine
Funktion
parseTreeToTurtleProgram : String -> List TurtleCommandHinweis. Das Umwandeln des Parsebaumes in das Turtle-Programm ist unangenehm. Insbesondere, weil Sie im Baum "vorausschauen" müssen, was Ihr Knoten für Kinder hat. Hier ist ein Code-Beispiel von mir, wo ich einen Knoten im Parsebaum, dessen erstes Kind ein "Move"-Command ist, in ein TurtleProgram umwandle:
Branch Grammar.Command [ Leaf (Lexer.CommandName "pen"), Leaf (Lexer.Parameter color), Leaf Lexer.Semicolon ] ->
Result.Ok (Pen color)
Beachten Sie, dass der Ausdruck in dieser Pattern-Matching-Zeile sehr verschachtelt ist. Insbesondere wird hier gematcht:
-
ein innerer Knoten (also
Branch), der mit nicht NichtterminalGrammar.Commandbeschriftet ist und - der drei Kinderknoten hat, die alle Blätter sind
Leafund
Bevor wir das Programm in eine Svg-Grafik übersetzen, wollen wir noch eine Sache erledigen:
das Programm glattstreichen. Damit meine ich, dass wir einen TurtleCommand
der Form
Repeat 5 listübersetzen in die Liste
list ++ list ++ list ++ list ++ list
TurtleProgram.elm eine Funktion
straightenTurtleProgram : TurtleProgram -> TurtleProgramdie ein Turtle-Programm in ein äquivalentes ohne
Repeat
übersetzt, indem sie die Repeat-Operationen ausführt, das
zu Wiederholende also tatsächlich wiederholt.
Abgabeformat: die Datei TurtleProgram.elm, nun mit
der gewünschten Funktion.
4. Das Programm als Svg zeichnen
In Elm gibt es den DatentypSvg msg, der Svg-Elemente in der Html-Seite darstellt (die
dann gezeichnet werden können). Der folgende Code erzeugt ein Svg-Objekt, ein rotes Geradensegment
mit Dicke 1.5 darstellt:
Svg.line
[ Svg.Attributes.x1 "100"
, Svg.Attributes.y1 "0.5"
, Svg.Attributes.x2 "300"
, Svg.Attributes.y2 "200"
, Svg.Attributes.stroke "red"
, Svg.Attributes.strokeWidth "1.5"
]
[]
Die Signatur ist
Svg.line : List (Svg.Attribute msg) -> List (Svg msg) -> Svg msgMit Hilfe dieser Funktion können Sie nun Ihr Turtle-Programm in eine Liste von Svg-Elementen übersetzen.
TurtleProgram.elm eine Funktion
turtleProgramToSvg : TurtleProgram -> List (Svg smg)
Abgabeformat: die Datei TurtleProgram.elm mit
der gewünschten Funktion.
Nun müssen Sie noch alles zusammenflicken. In der Datei DrawLR0Parser.elm sehen Sie, wie ich Svg-Objekte zeichne. Die entsprechende Code-Zeile ist
ZoomSvg.view model.svgCanvas [] dieListeIhrerSvgObjekte
DrawTurtle.elm auf Basis
meiner Datei DrawLR0Parser.elm,
die alles zusammenführt: Sie können hier ein Turtle-Programm eingeben, auf Draw
klicken
und dann wird auf dem SvgCanvas das Ergebnis gezeichnet.
Abgabeformat: die Datei DrawTurtle.elm, nun mit
der gewünschten Funktion.
5. Challenge: von kontextfreier Grammatik zum DK-Automaten
Mittlerweile haben Sie bestimmt festgestellt, dass es sehr mühsam sein kann,
den DK-Automaten per Hand auf dem Papier zu konstruieren. In diesem
Abschnitt schreiben wir eine Elm-Funktion, die aus einer gegebenen kontextfreien
Grammatik automatisch den DK-Automaten baut. Als erstes
überlegen wir uns einen Datentyp für die
Zustände des DK-Automaten. Ein typischer Zustand wäre ja zum Beispiel
type alias DottedRule tt nt =
{ leftSide : nt
, beforeDot : List (Symbol tt nt)
, afterDot : List (Symbol tt nt)
}
und somit steht auch klar, was die Zustände unseres DK-Automaten sind:
type alias DKstate tt nt = List (DottedRule tt nt)
Wie bauen Sie jetzt daraus einen DK-Automaten? Naja, Sie müssen den gar nicht
explizit bauen, d.h. Sie müssen nicht unbedingt alle Zustände berechnen. Sie
können einfach die Funktionen
delta und whichReduction
implementieren.
Wie kommen Sie nun von einem DKstate zum Folgezustand,
wenn Sie ein Zeichen, beispielsweise

List.filter und List.map
hinkriegen. Leider ist es damit nicht getan; von closure:
- wenn
In unserem Fall ist die Relation die
Schreiben wir nun eine allgemeine Funktion closure, die die Hülle einer
Menge unter einer gegebenen Relation berechnet. Als erstes müssen wir uns
überlegen, wie wir Mengen darstellen:
- Mengen. Eine Menge stellen wir einfach als Liste dar:
List a. Wir müssen nun allerdings aufpassen, dass wir Elemente nicht mehrfach einfügen. MitList.member a listkönnen Sie überprüfen, obain der Liste vorkommt. Dies ist potentiell ineffizient, weil wir lineare Suche verwenden. Für leistungsfähige Anwendungen bräuchten wir eine Datenstruktur (Hashtable, B-Bäume etc.), um Mengen darzustellen. Für dieses Projekt ist die naive Implementierung mit Listen allerdings ausreichend schnell. - Relationen. Am praktiabelsten ist es, wenn wir eine
Relation auf Objekten mit Typ
aals Funktionrelation: a -> List adarstellen;relation xliefert dann die Liste aller Objekte
AbstractDKautomaton.elm, die den
Datentyp DottedRule und eine Funktion
epsilonFollowers : DottedRule tt nt -> List (DottedRule tt nt)Abgabeformat: die Datei DottedRule.elm.
Wie berechnet man nun eine Hülle im Allgemeinen, wenn man die Relation
relation : a -> List a gegeben hat?
Hier meine Empfehlung: unterhalten Sie zwei Listen closed und open.
Die Idee ist, dass closed diejenigen Elemente closed oder open ist.
Jetzt nehmen Sie ein Element closed und bestimmen per
Aufruf der Funktion relation die Menge der Folge-Elemente. Sie
fügen alle Folge-Elemente der Liste open hinzu und verschieben
open nach closed.
Allerdings müssen Sie aufpassen: wenn ein Element bereits in closed ist,
sollte es nicht mehr in open eingefügt werden, sonst haben Sie eine Endlosschleife.
closure : (a -> List a) -> List a -> List a
closure relation set =
...
Abgabeformat: eine Datei Closure.elm mit
der Funktion closure.
Jetzt können Sie eigentlich den DK-Automaten implementieren: der Zustand ist
eine Menge (in Elm: eine Liste) von Dotted Rules, und für die Zustandsübergangsfunktion
closure als Subroutine verwenden.
Jetzt brauchen Sie nur noch whichReduction zu implementieren, welches
Ihnen eine "abgearbeitete Dotted Rule"
AbstractDKautomaton.elm die Funktionen
deltaGeneral : (ContextFreeGrammar tt nt) -> (DKstate tt nt) -> (Symbol tt nt) -> (DKstate tt nt) whichReductionGeneral : (ContextFreeGrammar tt nt) -> (DKstate tt nt) -> Maybe (Production tt nt)und schließlich eine Funkton
buildDKautomaton : ContextFreeGrammar tt nt -> DKAutomaton tt nt (DKstate tt nt)die aus einer kontextfreien Grammatik den fertigen DK-Automaten baut.
Abgabeformat: die Datei AbstractDKautomaton.elm.