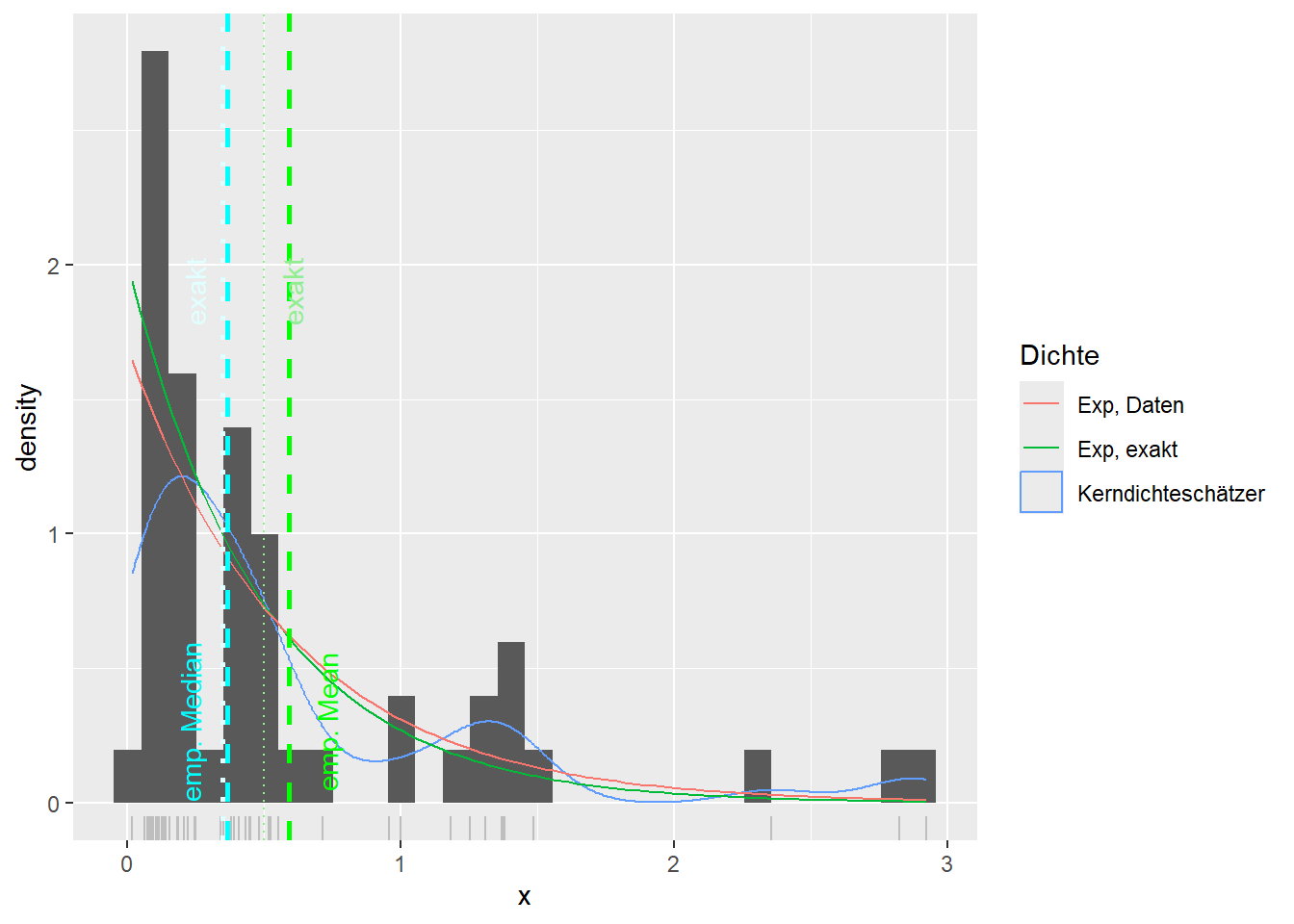
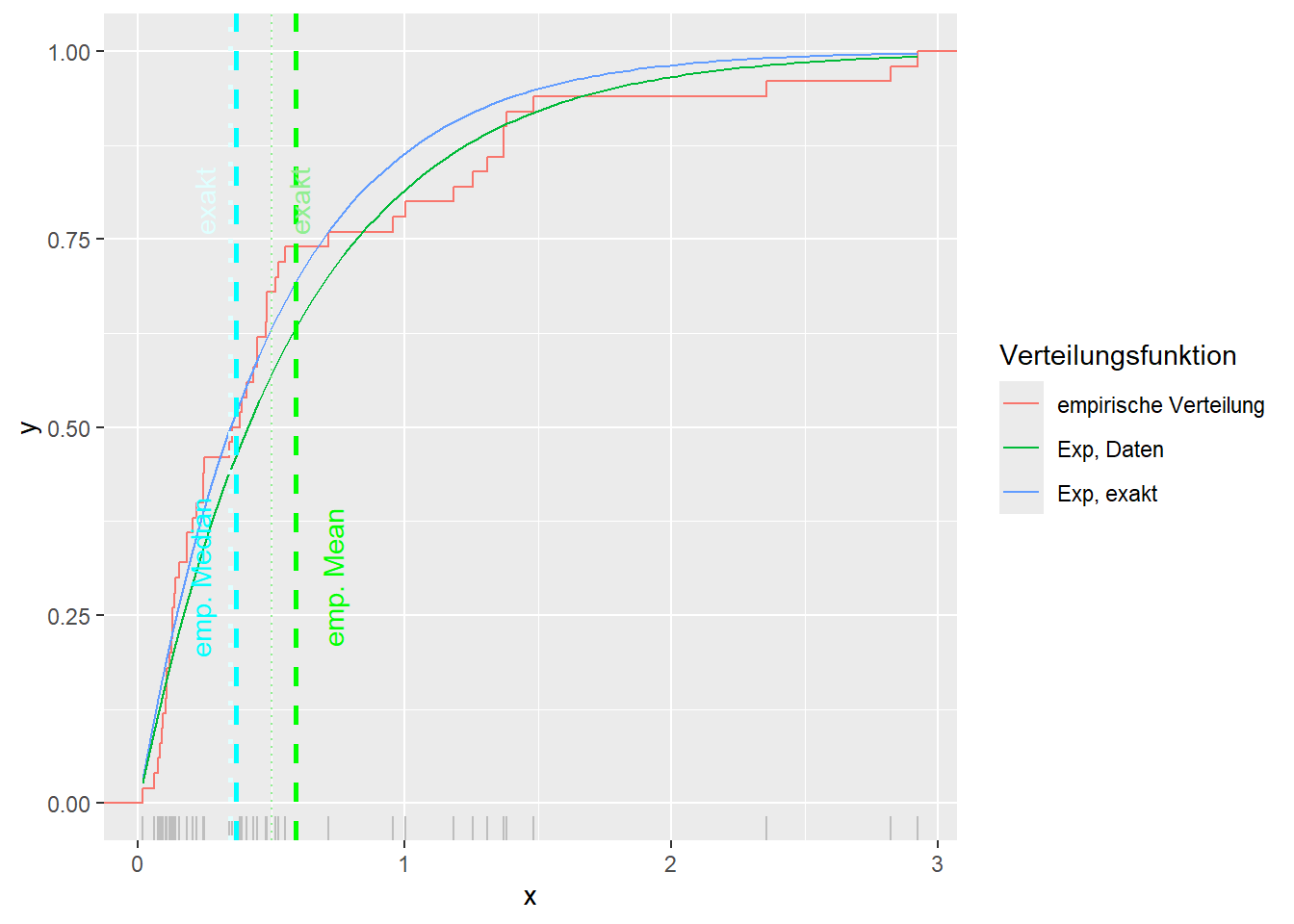
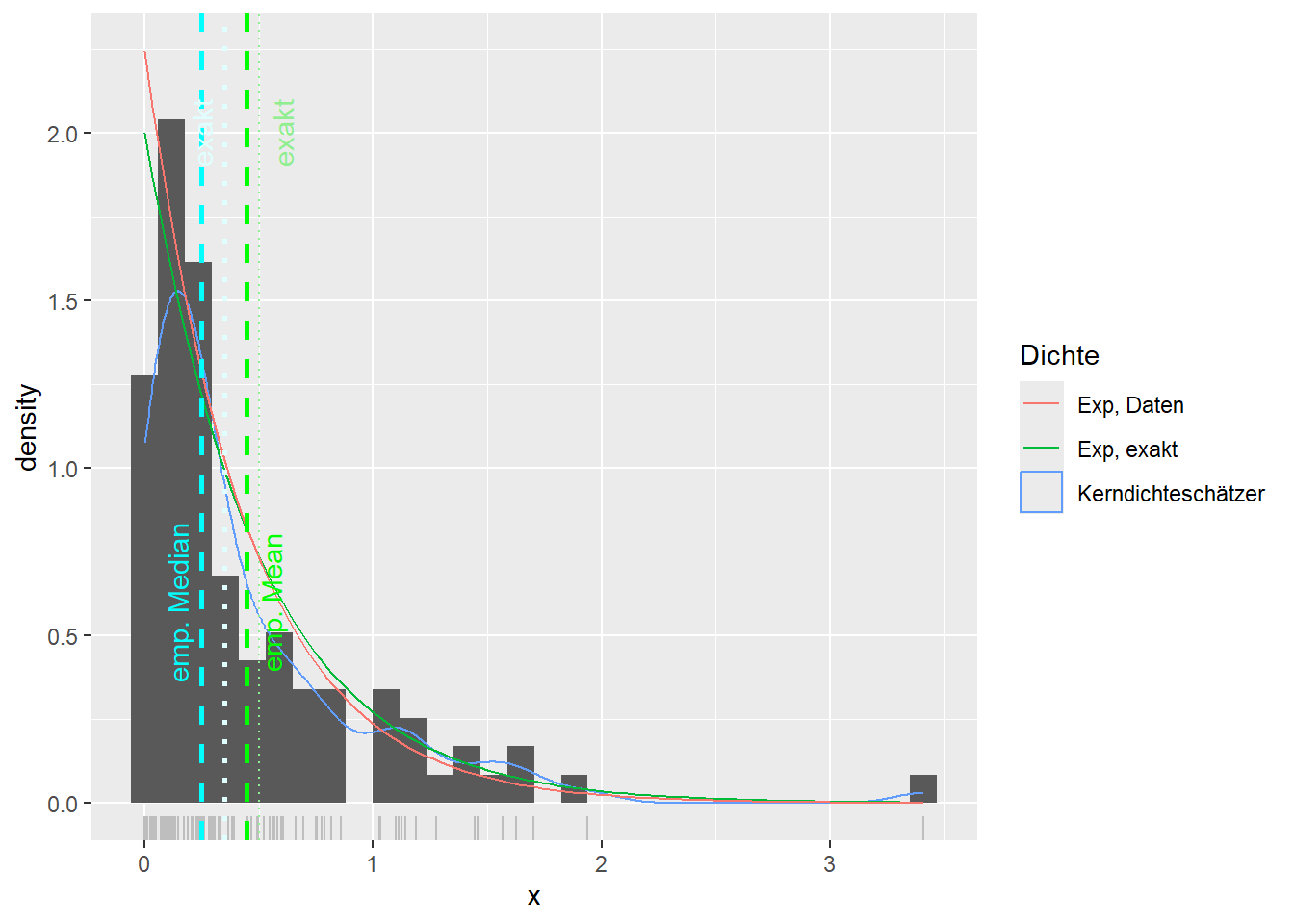
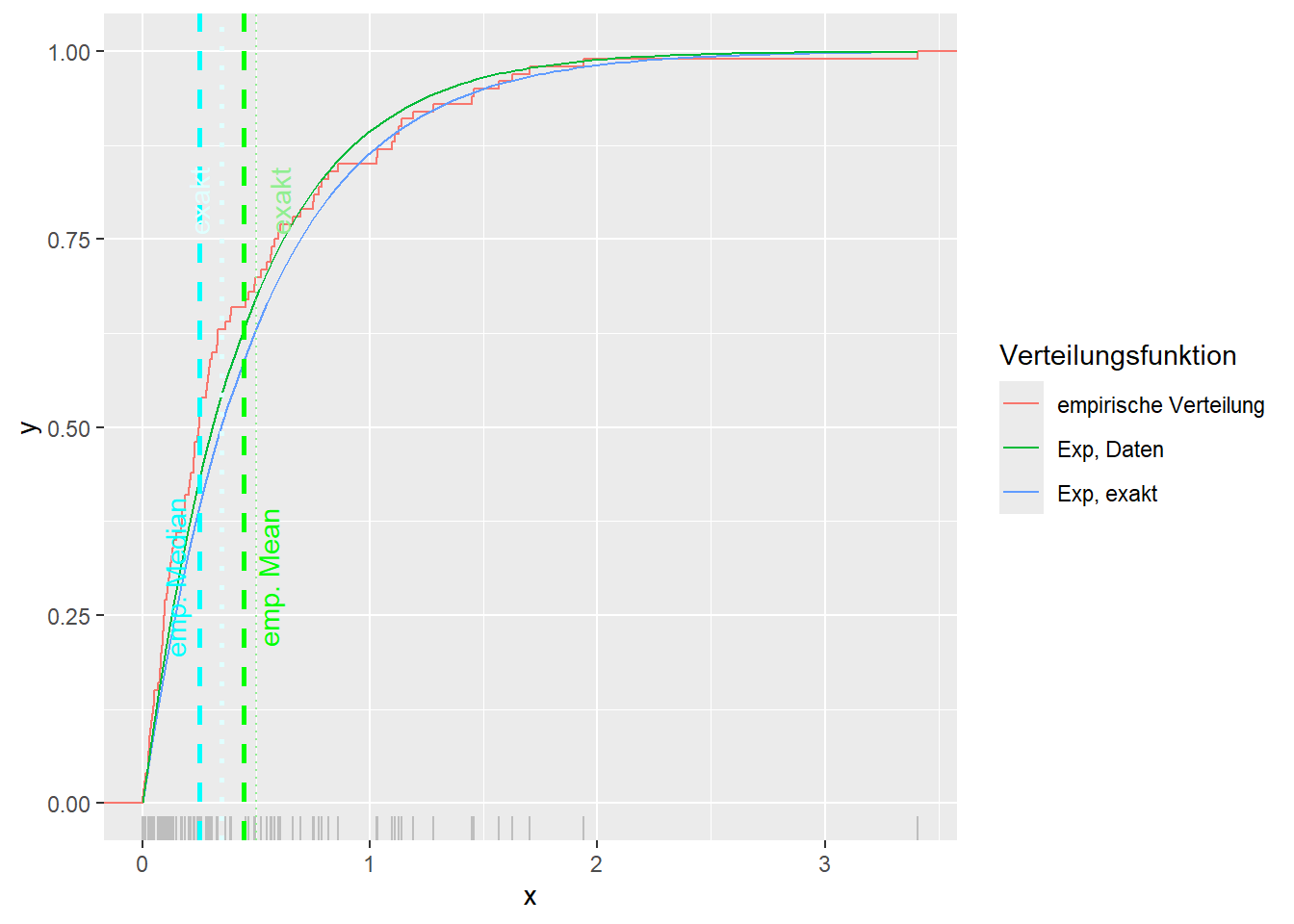
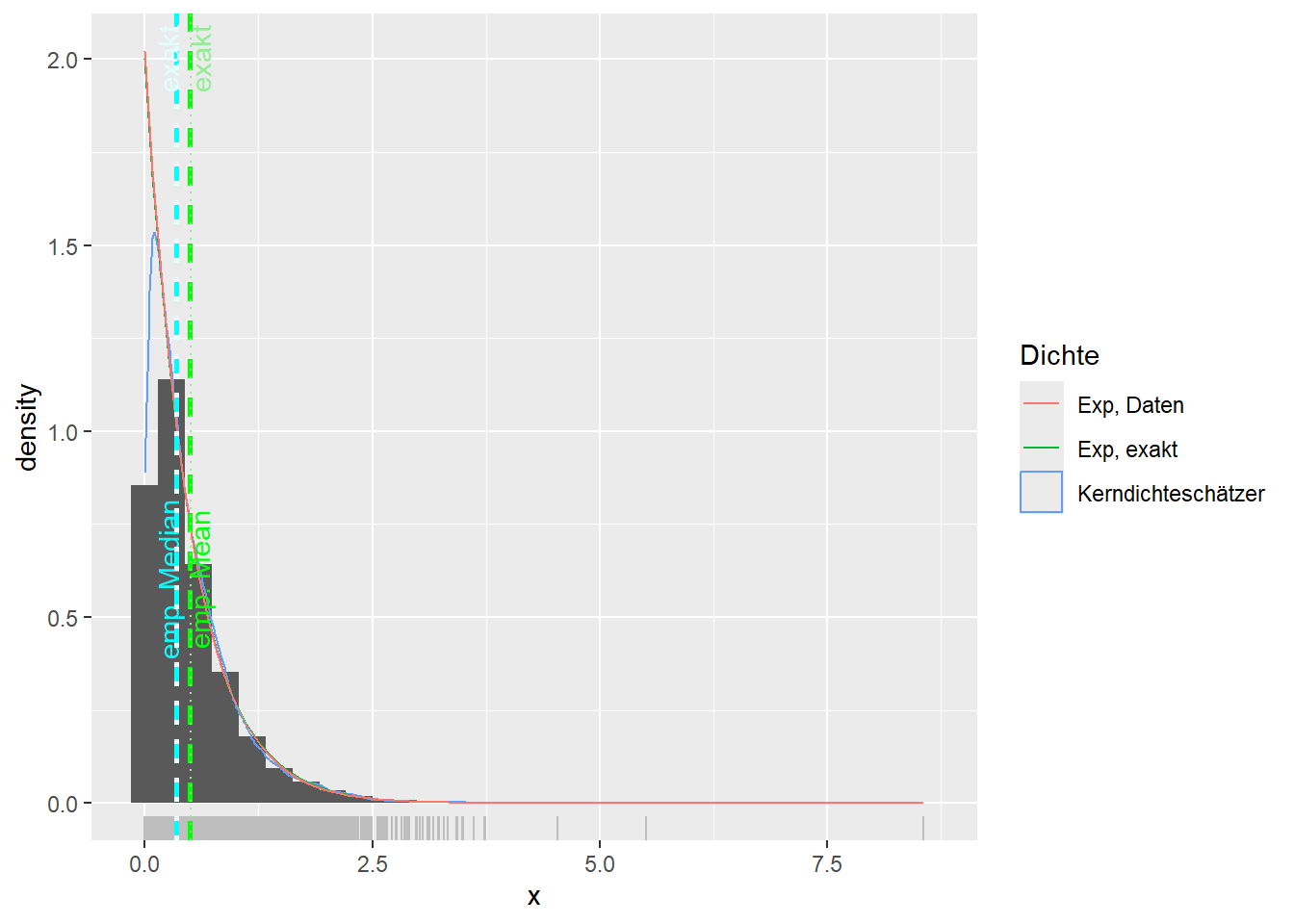
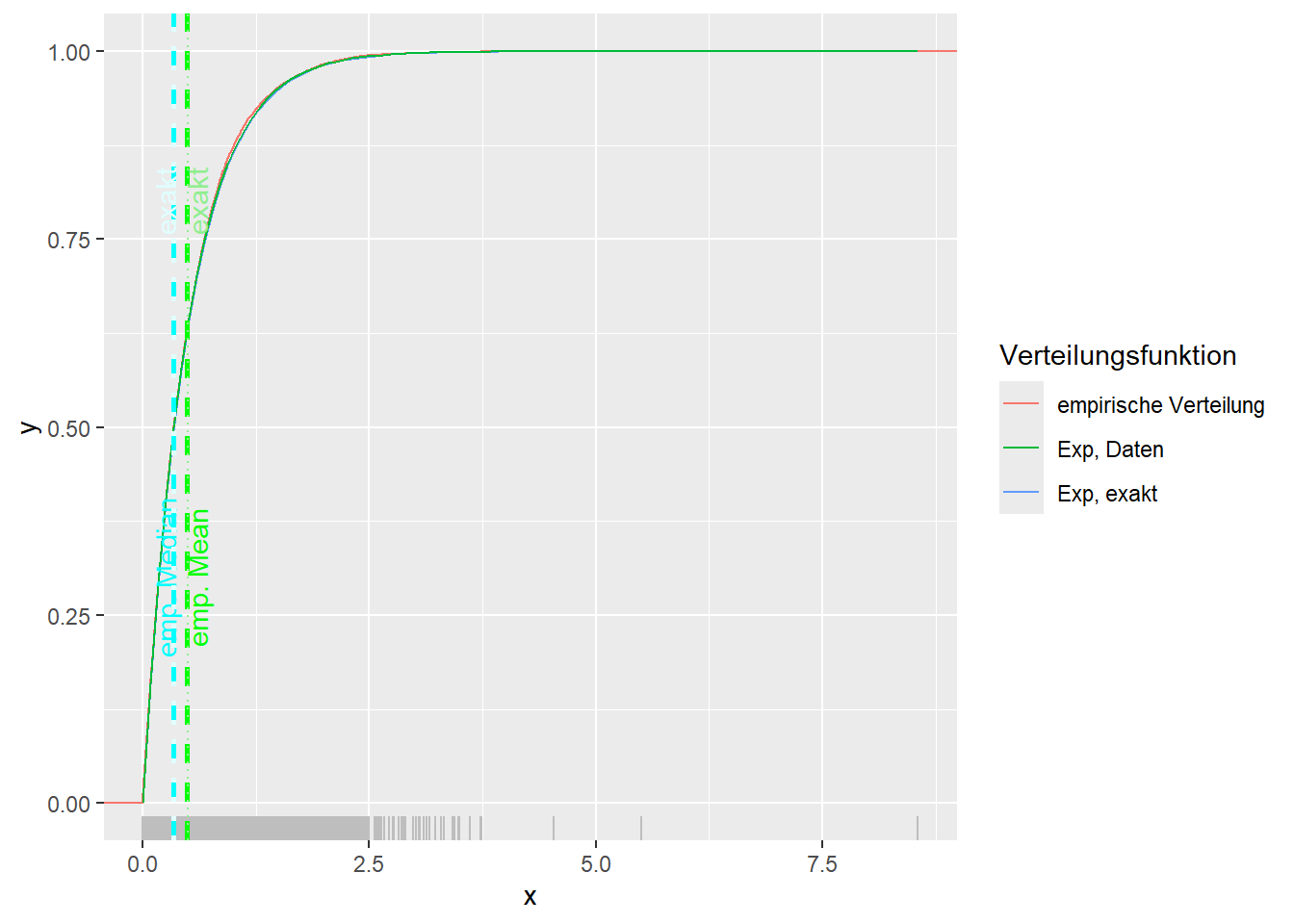
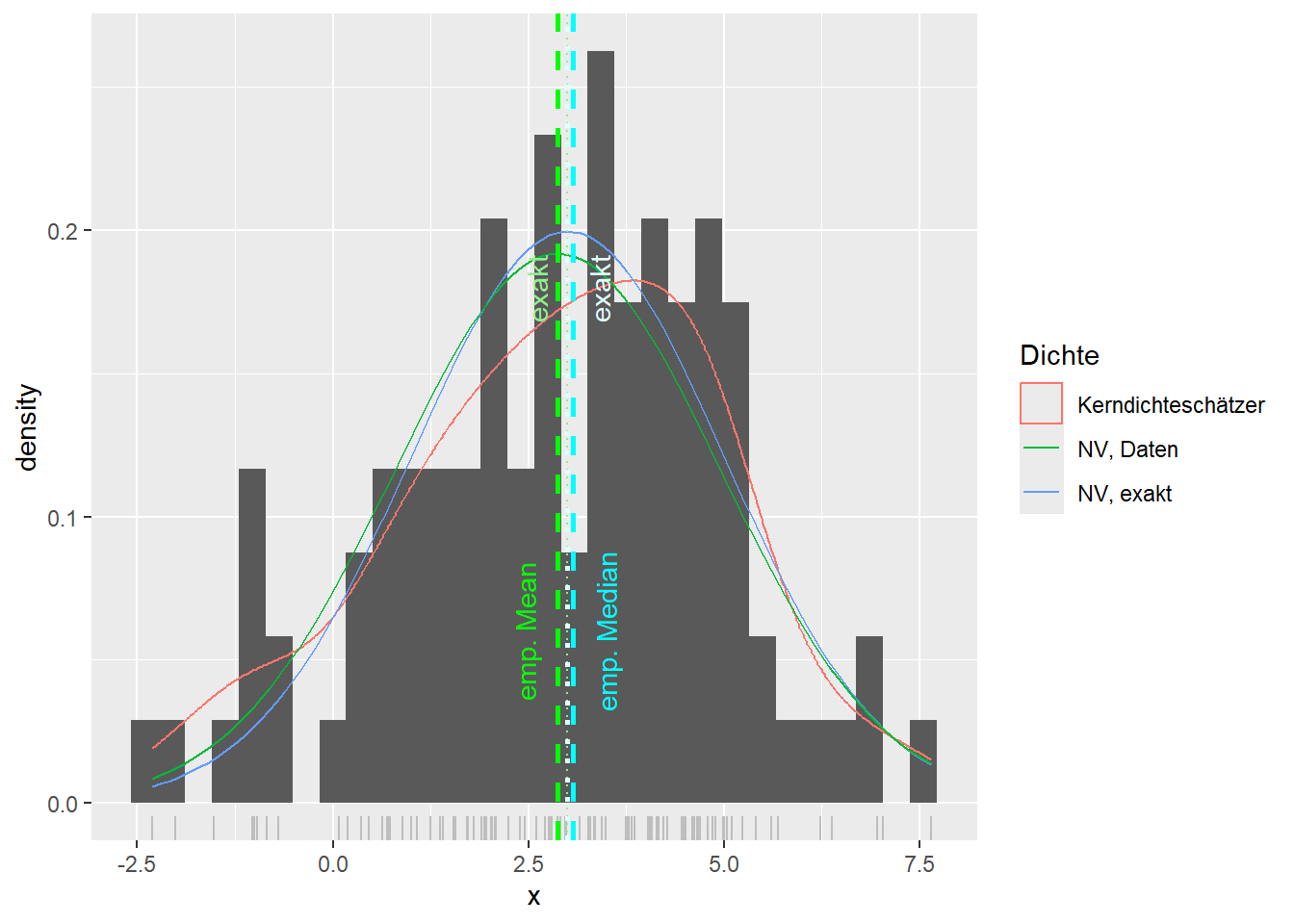
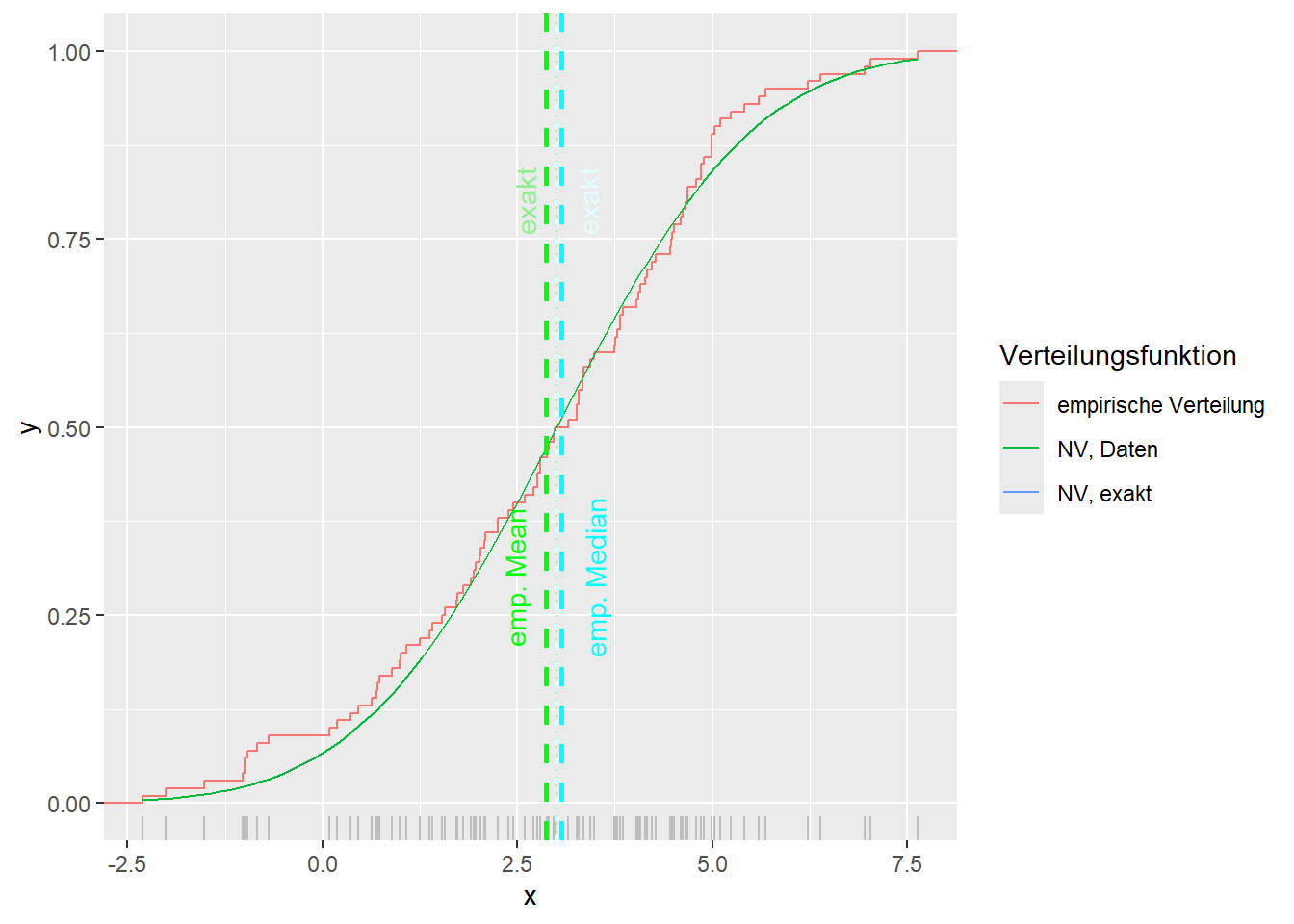
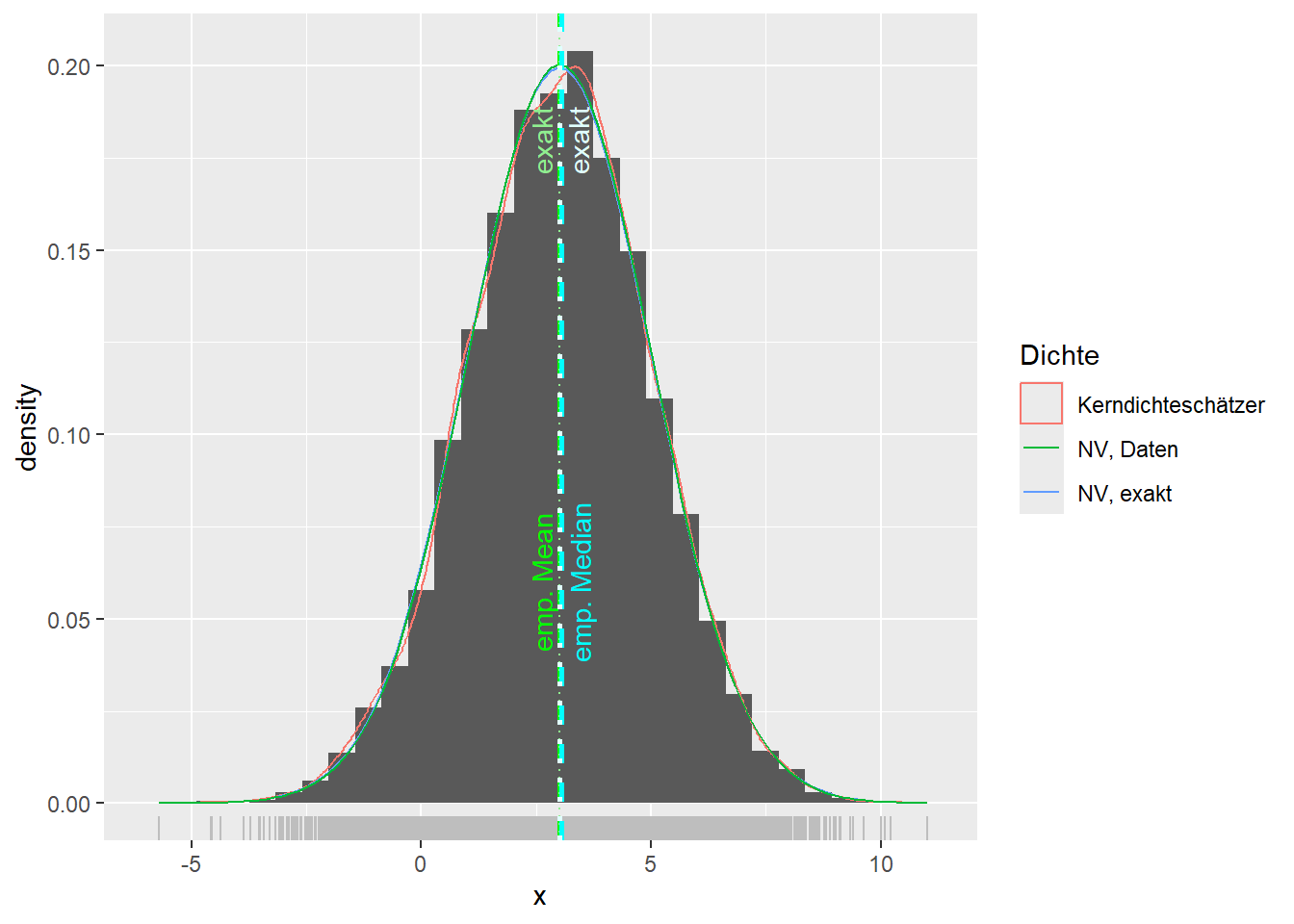
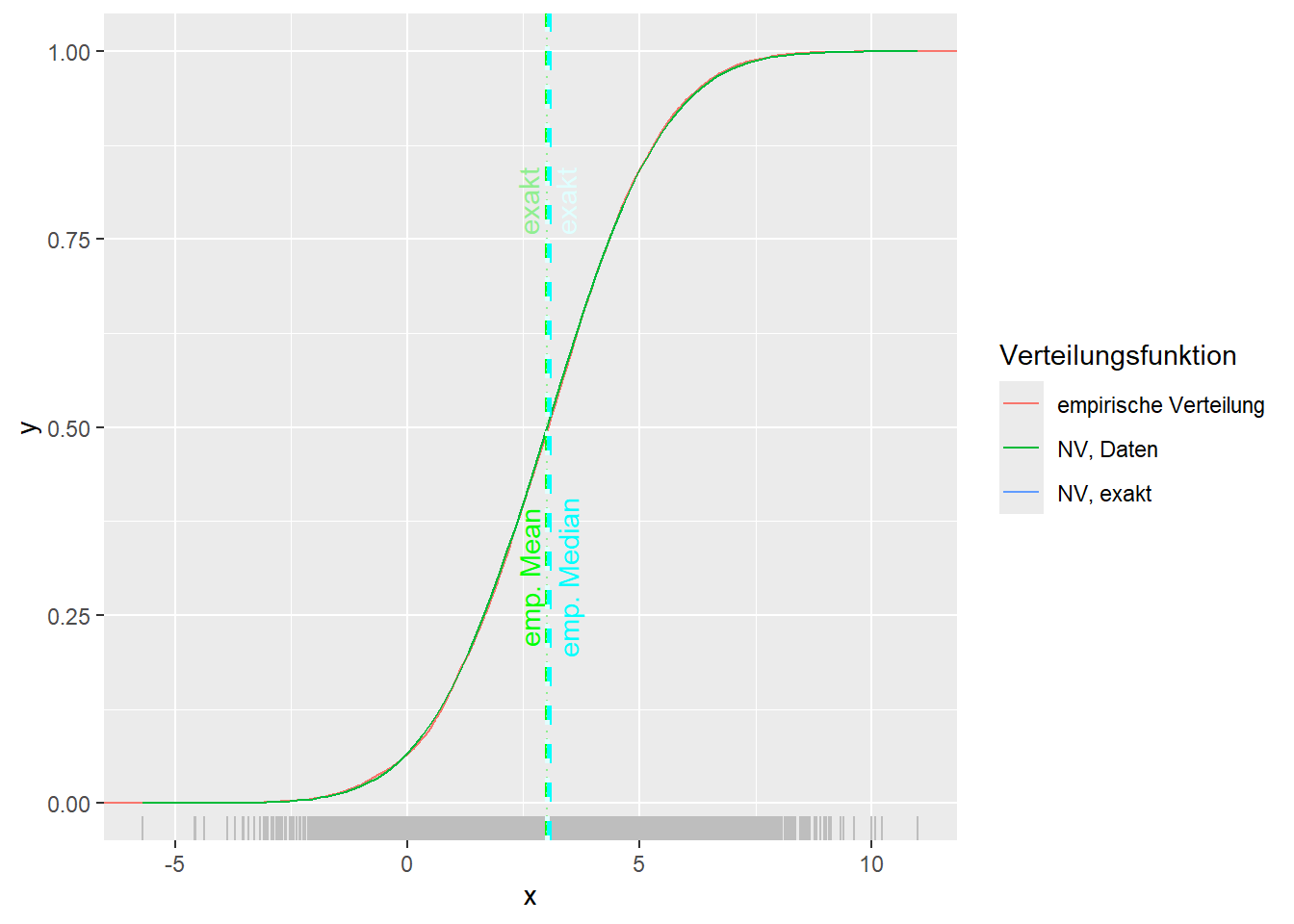
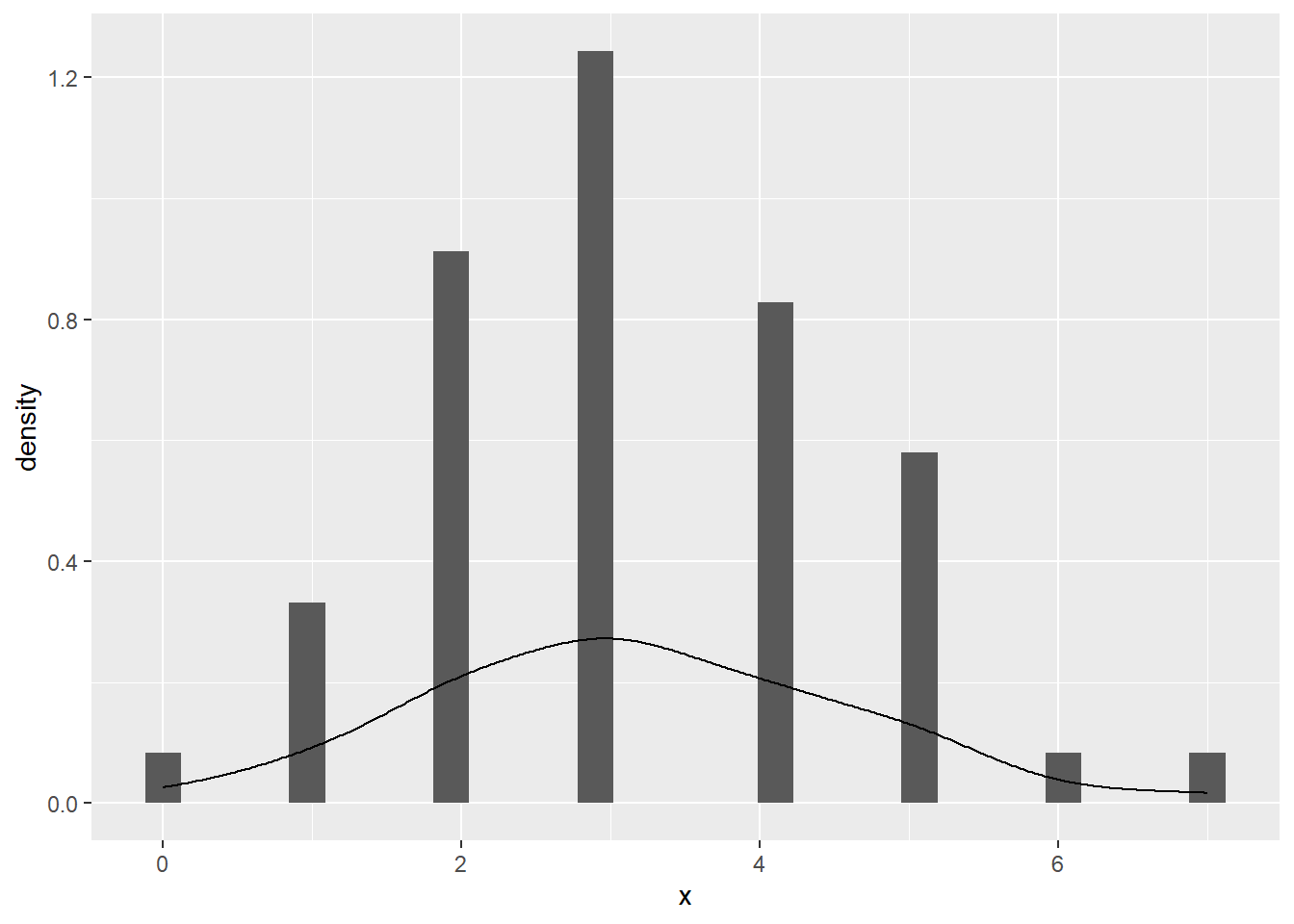
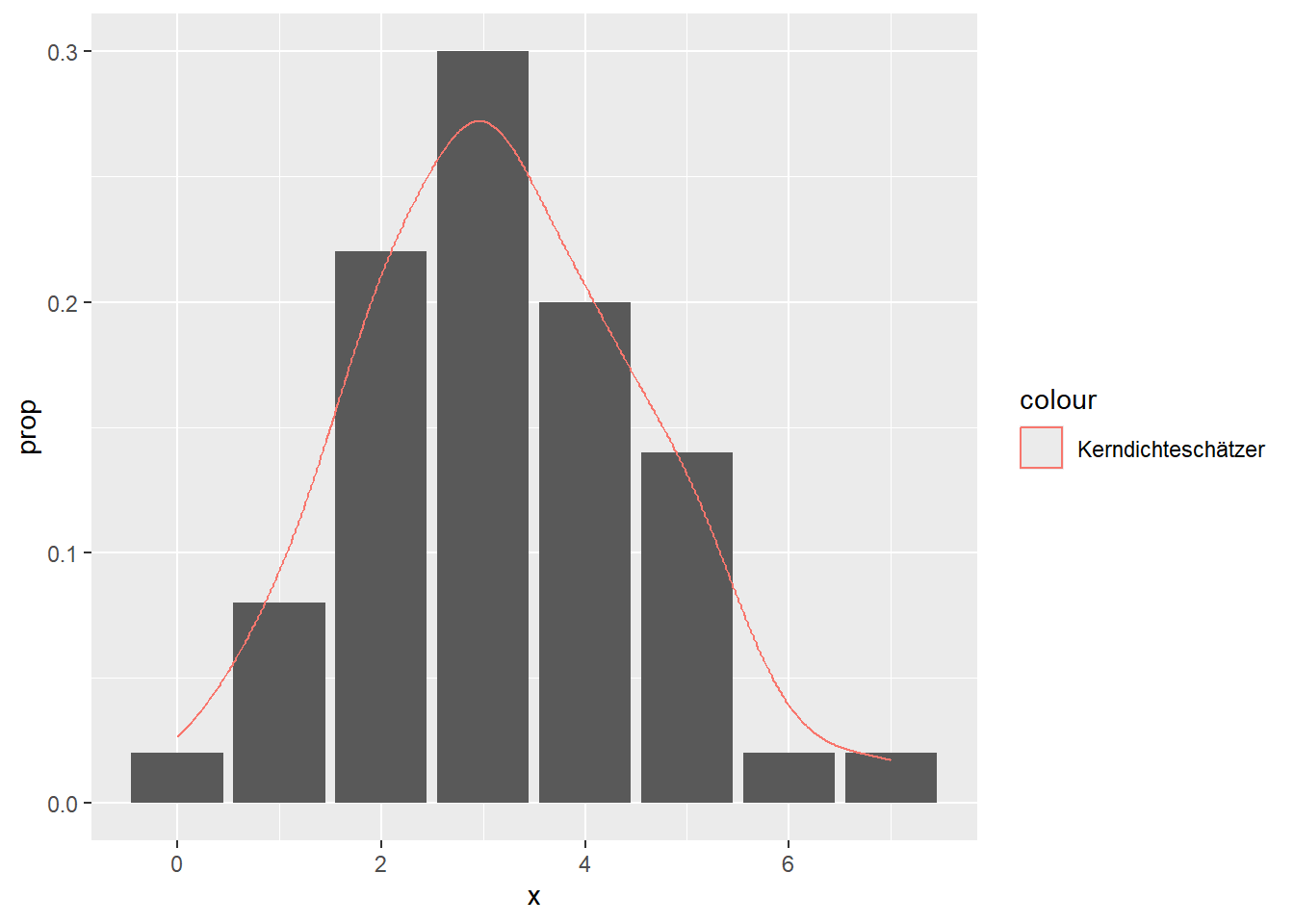
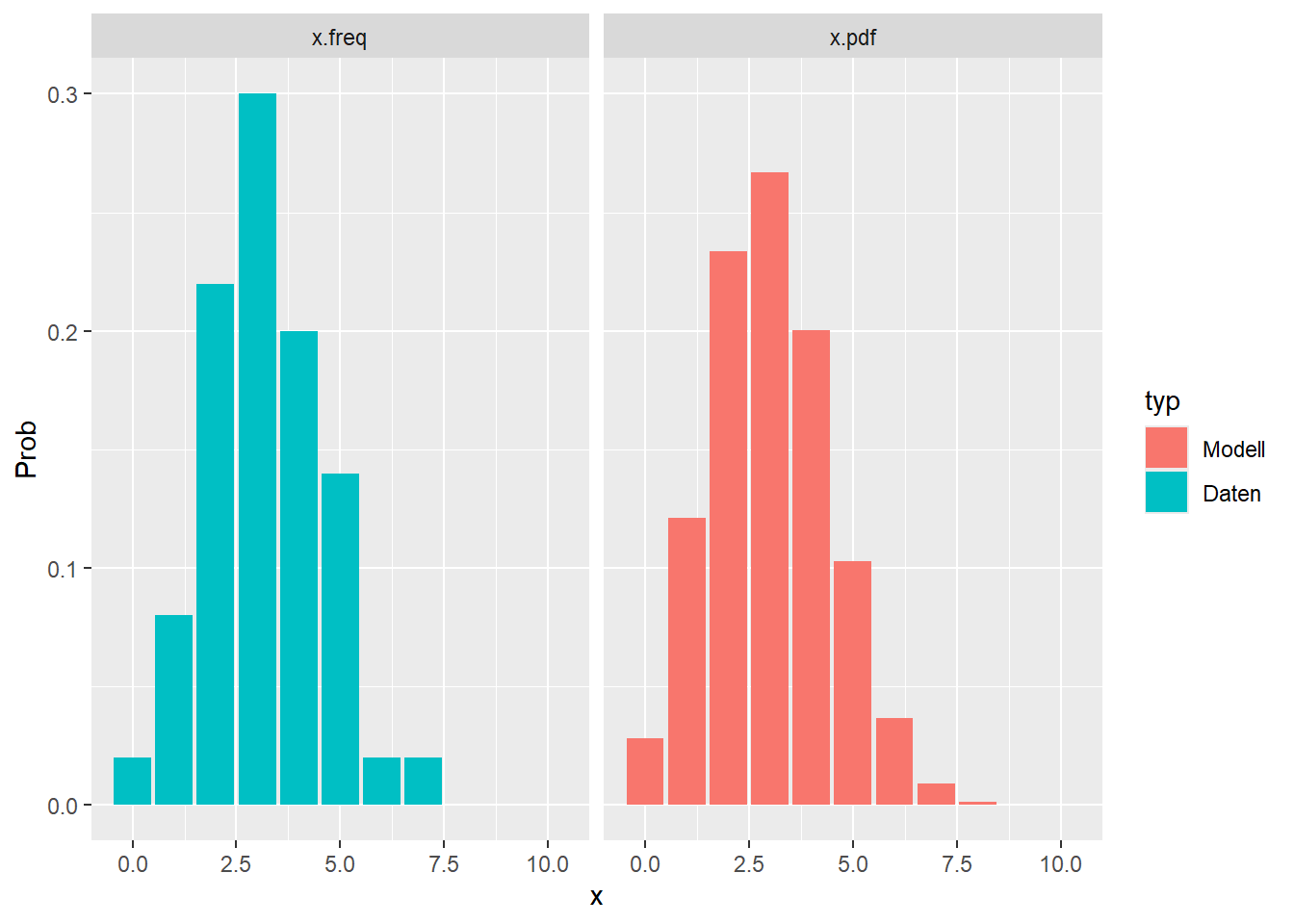
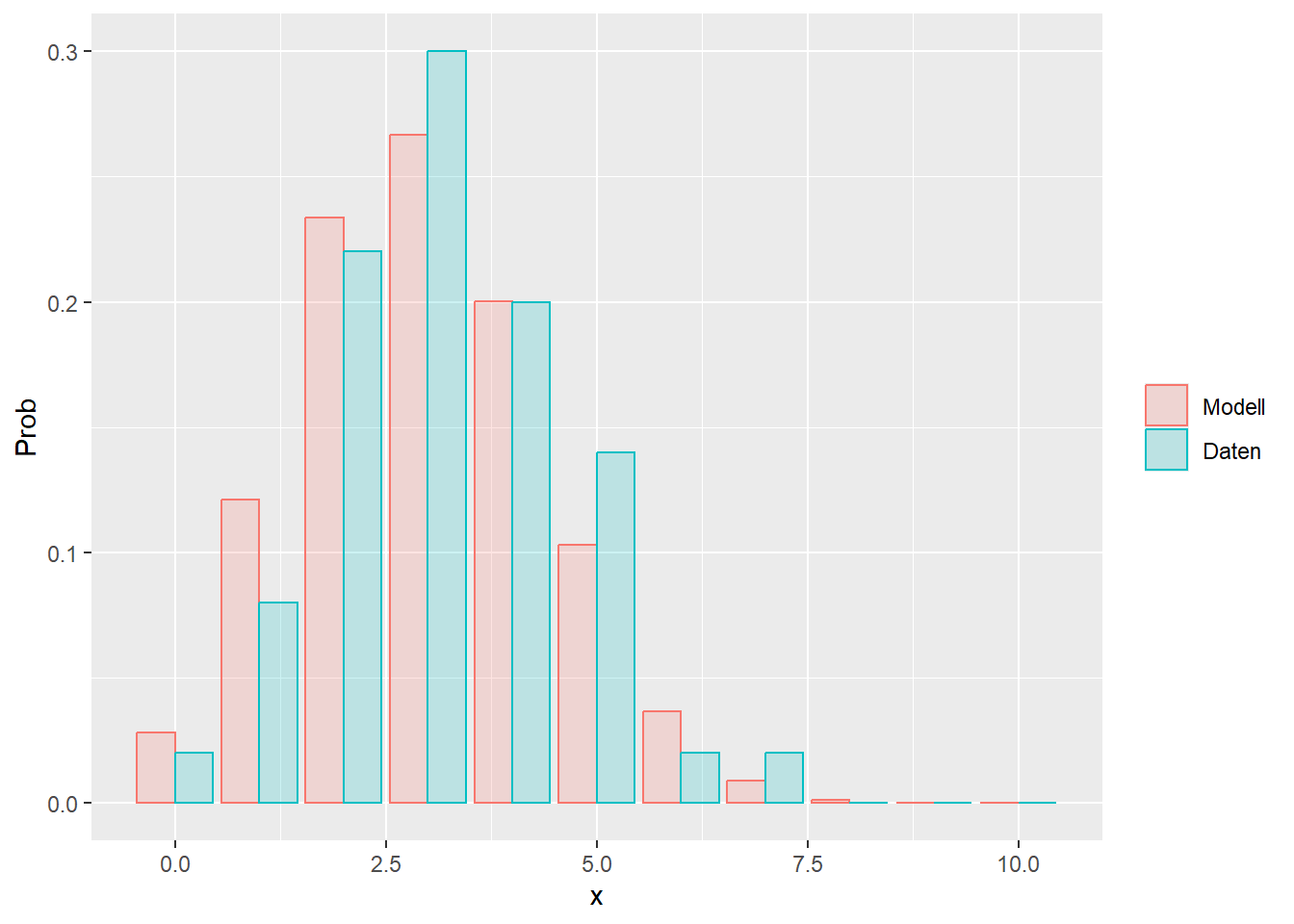
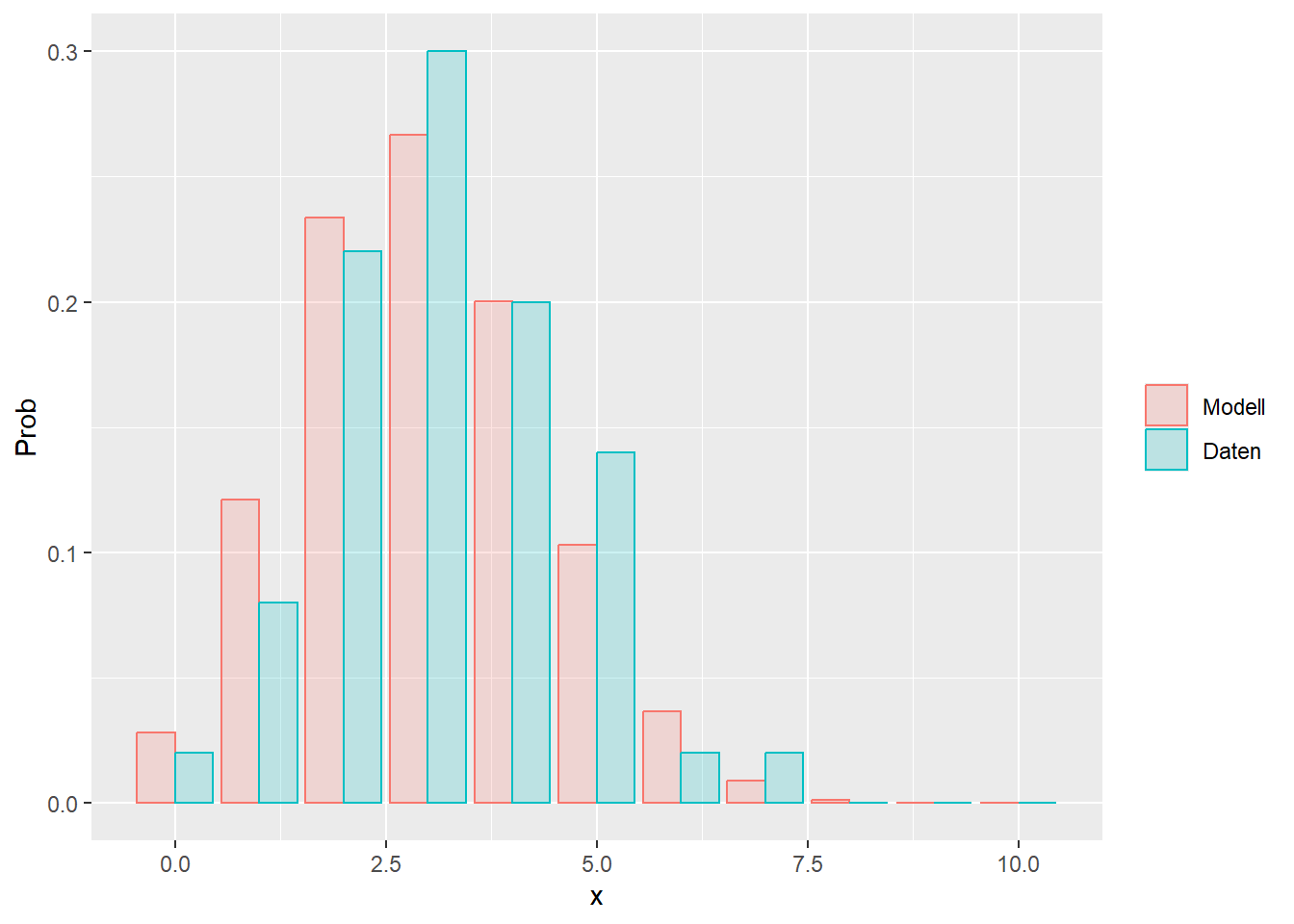
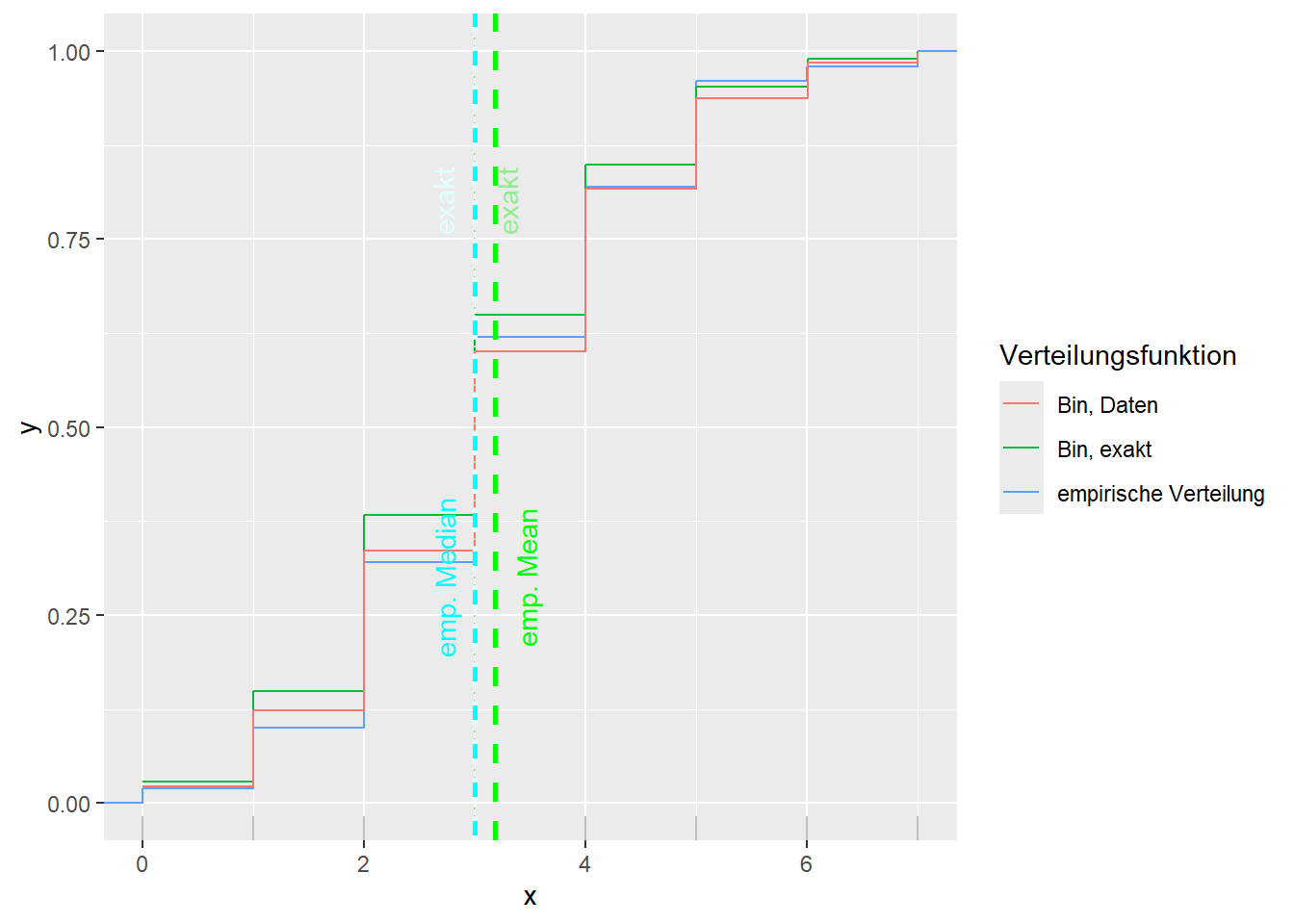
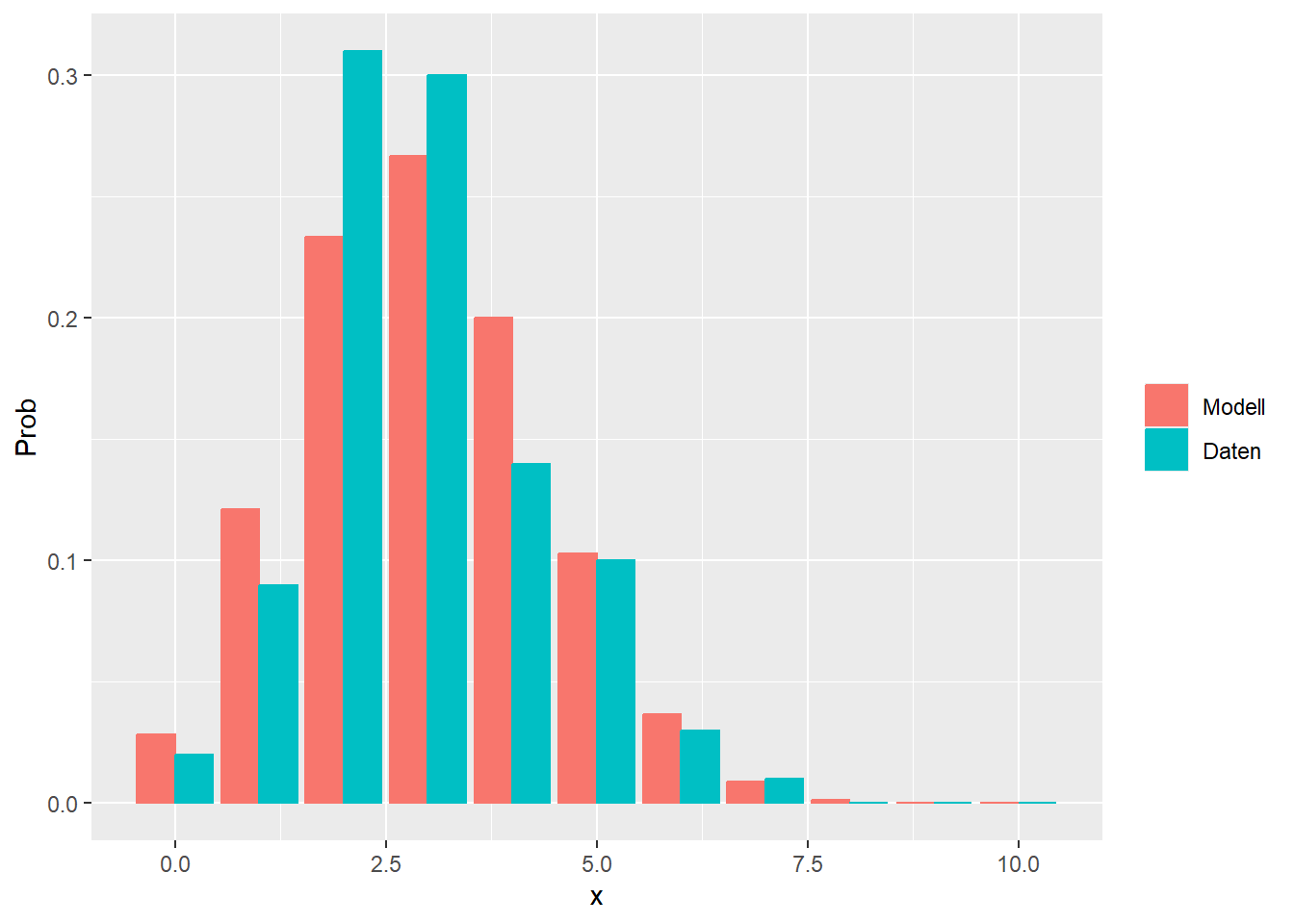
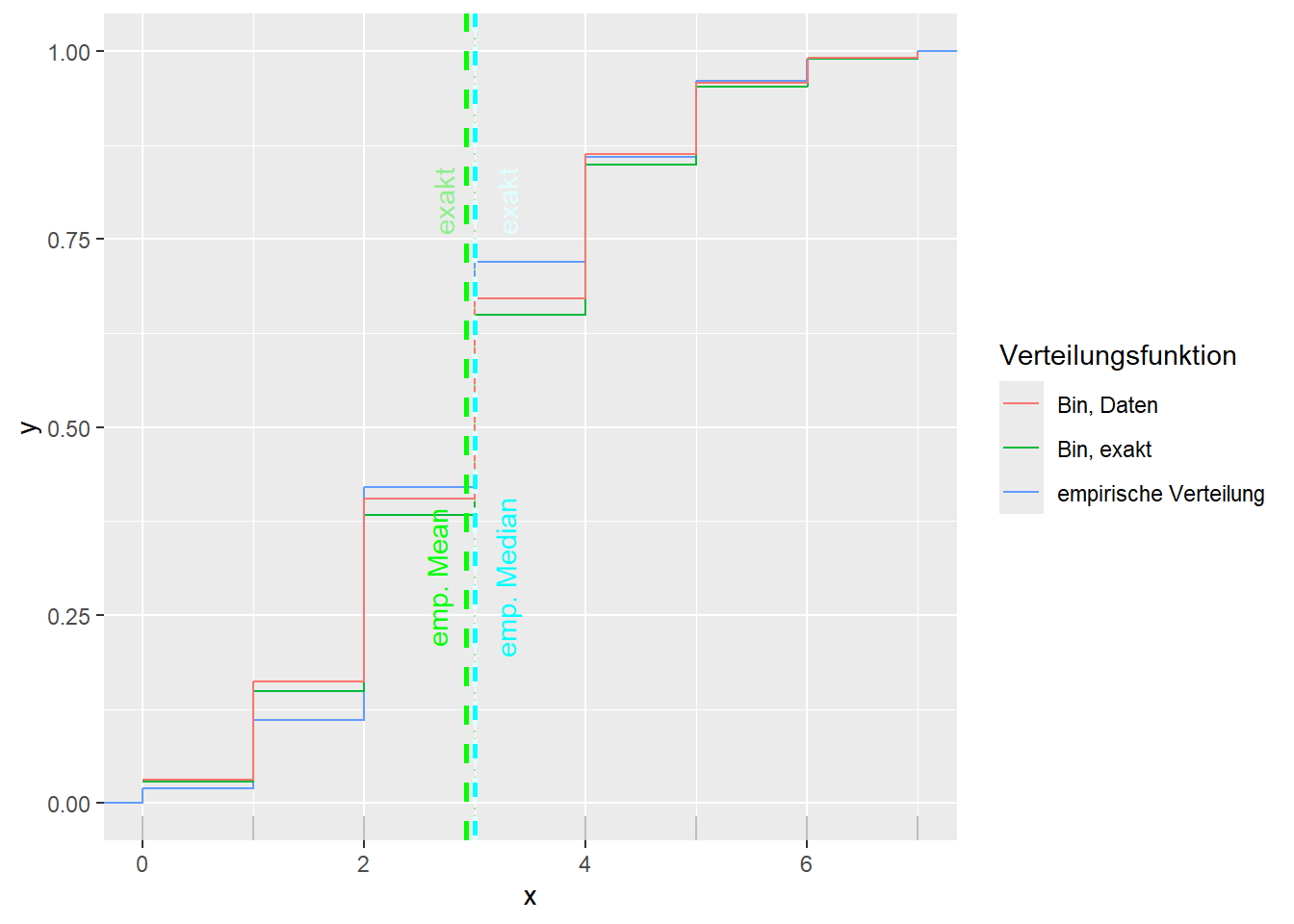
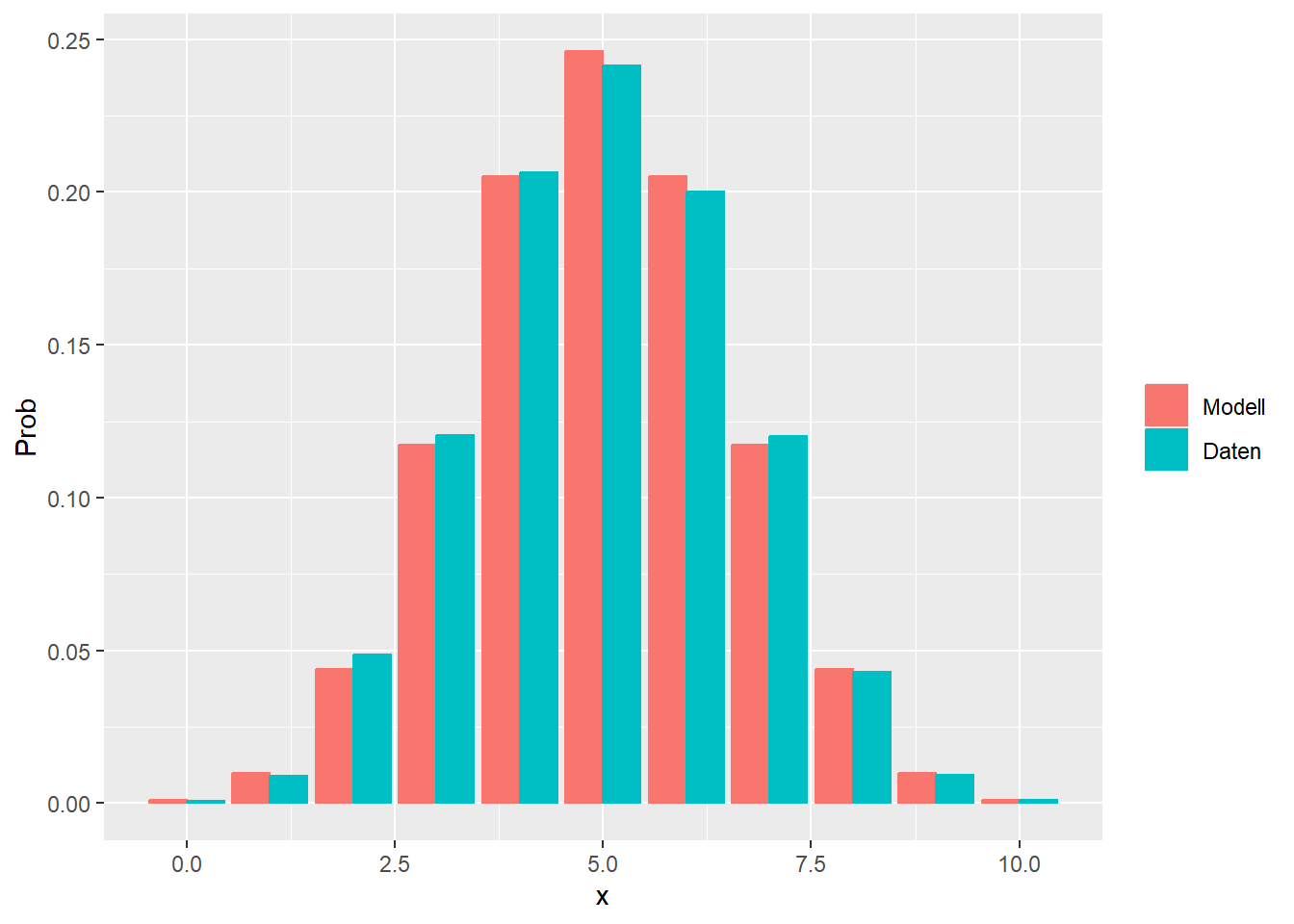
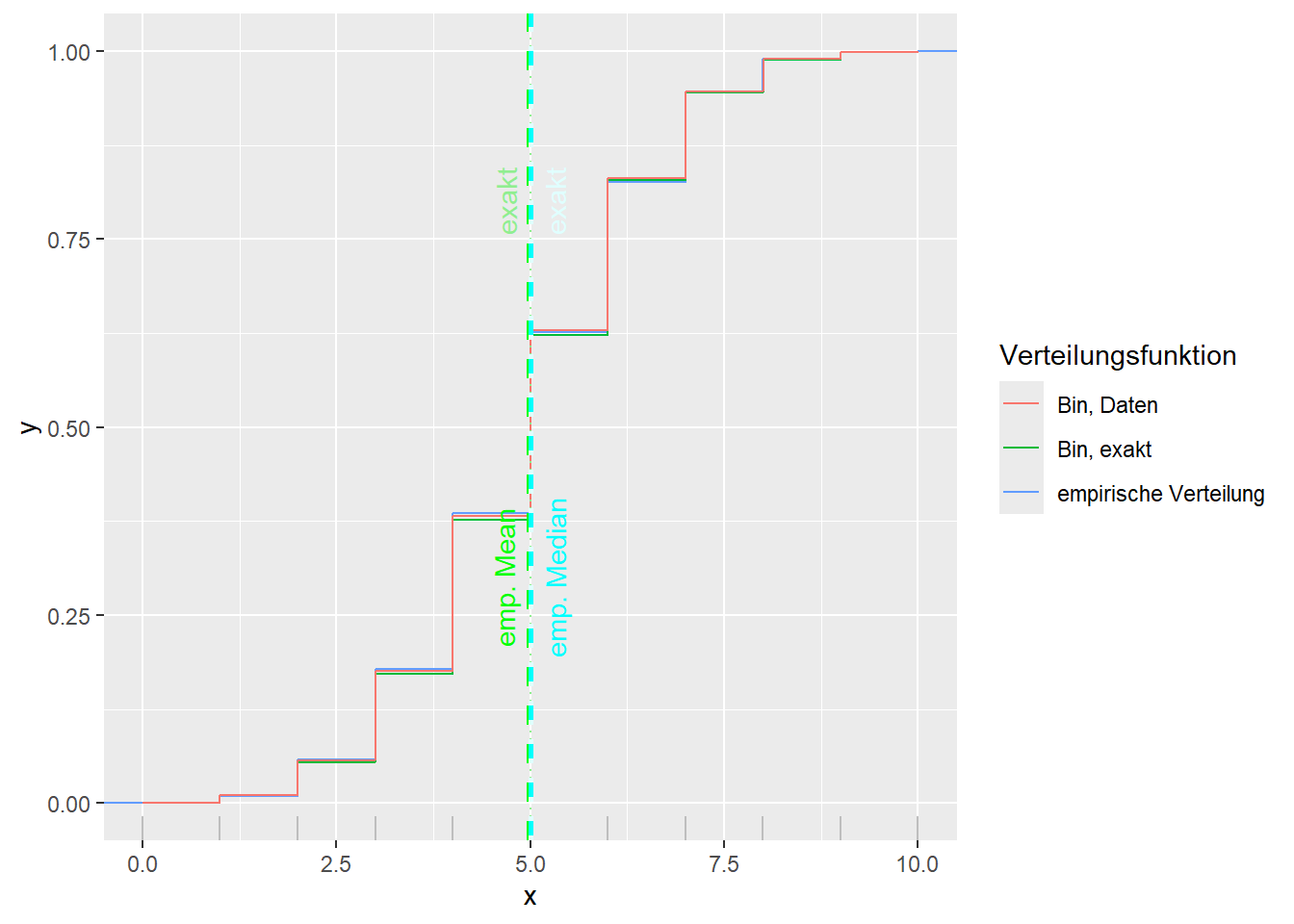
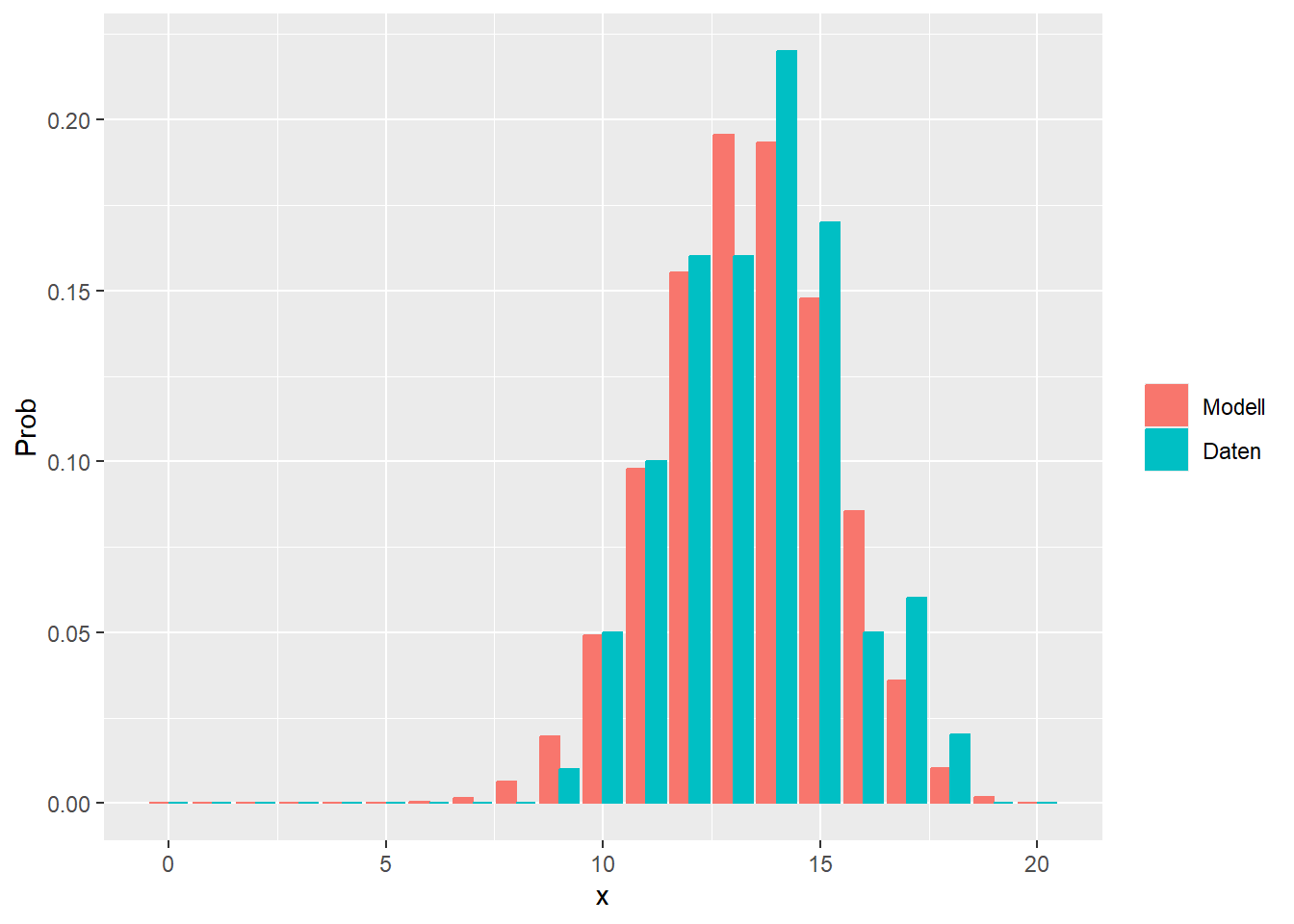
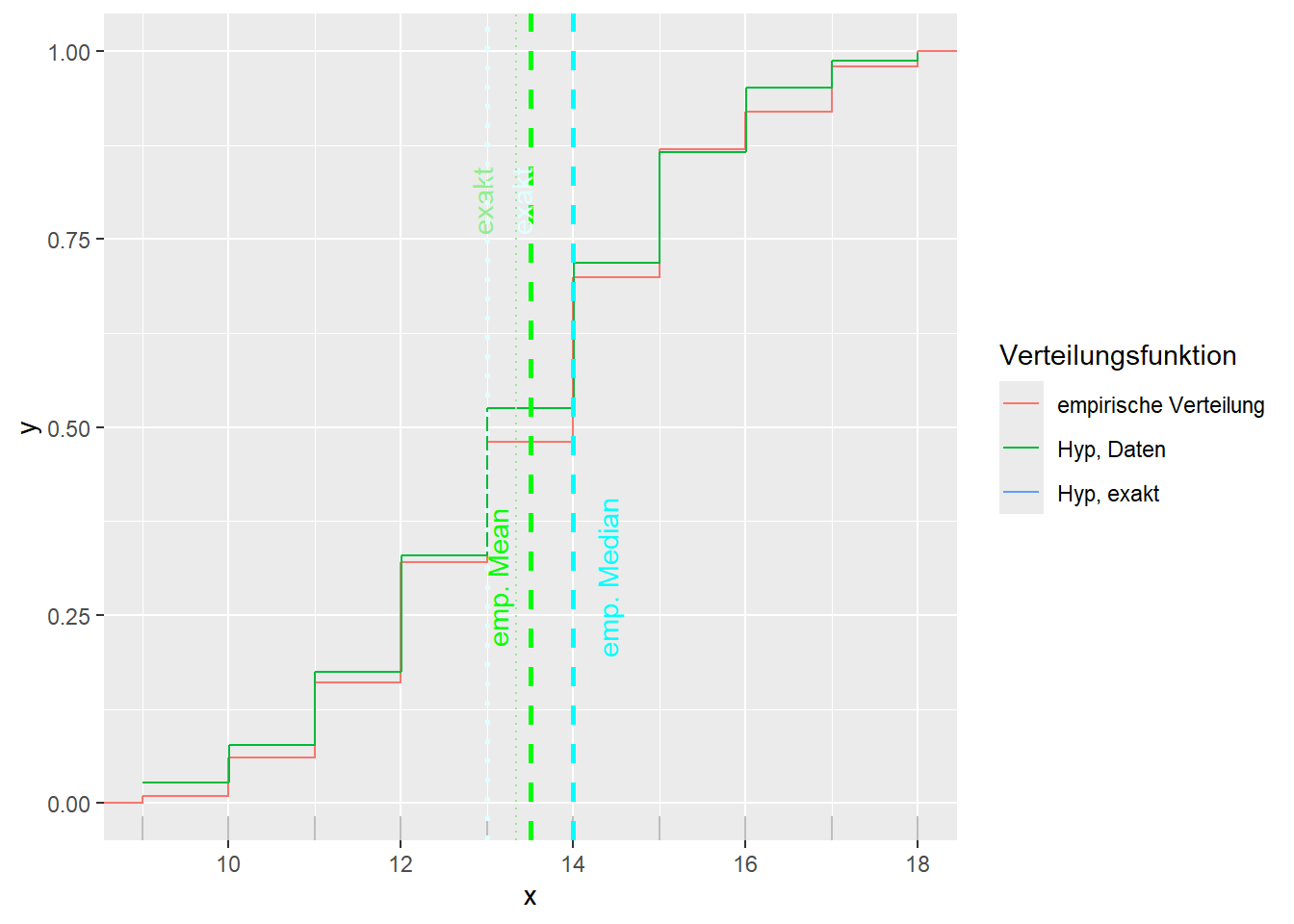
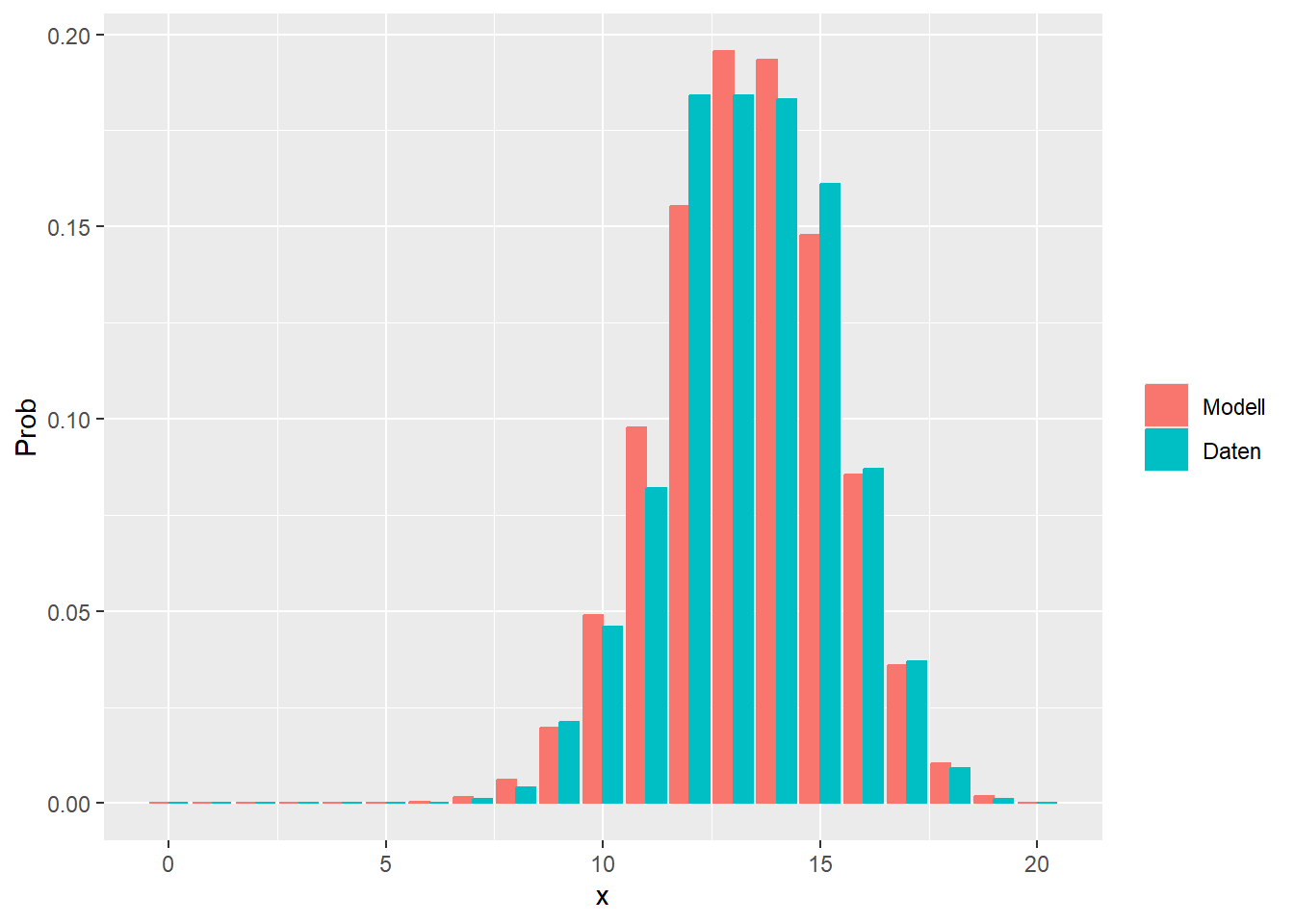
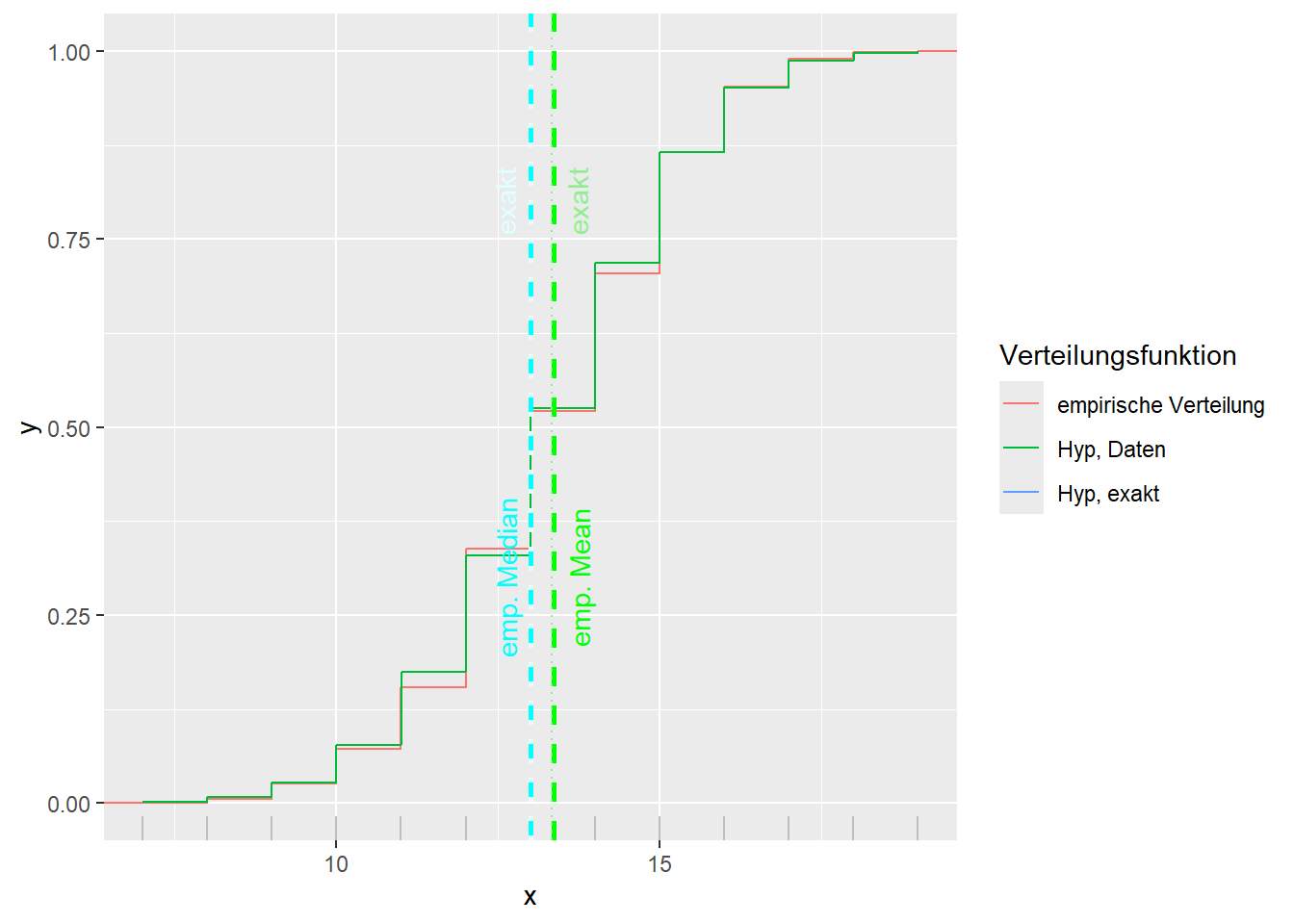
Illustration von Verteilungen

1 Vorbereitung: Arbeiten mit Statistiksoftware R

R: https://www.r-project.org/ Empfehlung Editor: RStudio auf https://posit.co/products/open-source/rstudio/

Installation von R-Zusatzpaketen, falls diese noch nicht installiert sind, und laden der Pakete

wants <- c("tidyverse", "latex2exp")
has <- wants %in% rownames(installed.packages())
if (any(!has)) install.packages(wants[!has])

# fuer schoene Grafiken, Stichwort ggplot
library("tidyverse")

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(latex2exp)

Im Folgenden simulieren wir Stichproben vom Umfang n zu den jeweiligen Verteilungen und stellen die empirischen Verteilungen der Stichproben gegen die theoretischen Verteilungen graphisch dar…

n <- 50

2 Stetige Verteilungen

2.1 Exponentialverteilung

mu <- 2

(exakt.mean <- 1 / mu)

[1] 0.5

(exakt.var <- 1 / (mu^2))

[1] 0.25

(exakt.median <- log(2) / mu)

[1] 0.3465736

# simulieren Daten nach Exponentialverteilung
x <- rexp(n = n, rate = mu)
x.data <- tibble(x)

# empirische Masszahlen
(x.mean <- mean(x))

[1] 0.59094

(x.median <- median(x))

[1] 0.3658964

(x.sd <- sd(x))

[1] 0.6846283

# nur fuer Graphiken
d <- x.mean - x.median
d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

ggplot(data = x.data, aes(x)) +
  geom_histogram(aes(y = after_stat(density))) + # Histogramm der relativen Haeufigkeiten
  # geom_rug(aes(col="Daten")) +
  geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
  geom_density(aes(col = "Kerndichteschätzer")) +
  stat_function(fun = dexp, args = list(rate = mu), aes(col = "Exp, exakt")) +
  stat_function(fun = dexp, args = list(rate = 1 / x.mean), aes(col = "Exp, Daten")) +
  # empirischer Mittelwert:
  geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
  annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
  # exakter Mittelwert
  geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
  annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 1.9, colour = "lightgreen", angle = 90) +
  # empirischer Median
  geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
  annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
  # exakter Median
  geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
  annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 1.9, colour = "lightcyan", angle = 90) +
  labs(col = "Dichte")

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

ggplot(data = x.data, aes(x)) +
  stat_ecdf(aes(col = "empirische Verteilung")) +
  geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
  stat_function(fun = pexp, args = list(rate = mu), aes(col = "Exp, exakt")) +
  stat_function(fun = pexp, args = list(rate = 1 / x.mean), aes(col = "Exp, Daten")) +
  labs(col = "Verteilungsfunktion") +
  # empirischer Mittelwert:
  geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
  annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
  # exakter Mittelwert
  geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
  annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
  # empirischer Median
  geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
  annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
  # exakter Median
  geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
  annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

Schreiben alles in eine Funktion für Exponentialverteilung…

sim_exp <- function(n = 50, mu = 2.0) {
  exakt.mean <- 1 / mu
  exakt.var <- 1 / (mu^2)
  exakt.median <- log(2) / mu

  # simulieren Daten nach Exponentialverteilung
  x <- rexp(n = n, rate = mu)
  x.data <- tibble(x)

  # empirische Masszahlen
  x.mean <- mean(x)
  x.median <- median(x)
  x.sd <- sd(x)

  # nur fuer Graphiken
  d <- x.mean - x.median
  d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
  d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

  max.dens <- mu

  graph.pdf <- ggplot(data = x.data, aes(x)) +
    geom_histogram(aes(y = after_stat(density))) + # Histogramm der relativen Haeufigkeiten
    # geom_rug(aes(col="Daten")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    geom_density(aes(col = "Kerndichteschätzer")) +
    stat_function(fun = dexp, args = list(rate = mu), aes(col = "Exp, exakt")) +
    stat_function(fun = dexp, args = list(rate = 1 / x.mean), aes(col = "Exp, Daten")) +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3 * max.dens, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 1.0 * max.dens, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3 * max.dens, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 1.0 * max.dens, colour = "lightcyan", angle = 90) +
    labs(col = "Dichte")

  print(graph.pdf)

  graph.cdf <- ggplot(data = x.data, aes(x)) +
    stat_ecdf(aes(col = "empirische Verteilung")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    stat_function(fun = pexp, args = list(rate = mu), aes(col = "Exp, exakt")) +
    stat_function(fun = pexp, args = list(rate = 1 / x.mean), aes(col = "Exp, Daten")) +
    labs(col = "Verteilungsfunktion") +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

  print(graph.cdf)

  # return(list(graph.pdf, graph.cdf))
}

sim_exp(n = 100, mu = 2)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

sim_exp(n = 10000, mu = 2)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

2.2 Normalverteilung

sim_normal <- function(n = 50, mu = 0.0, sigma = 1.0) {
  exakt.mean <- mu
  exakt.var <- sigma^2
  exakt.median <- qnorm(p = 0.5, mean = mu, sd = sigma)

  # simulieren Daten nach Normalverteilung
  x <- rnorm(n = n, mean = mu, sd = sigma)
  x.data <- tibble(x)

  # empirische Masszahlen
  x.mean <- mean(x)
  x.median <- median(x)
  x.sd <- sd(x)

  # nur fuer Graphiken
  d <- x.mean - x.median
  d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
  d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

  max.dens <- 1 / (sqrt(2 * pi) * sigma)

  graph.pdf <- ggplot(data = x.data, aes(x)) +
    geom_histogram(aes(y = after_stat(density))) + # Histogramm der relativen Haeufigkeiten
    # geom_rug(aes(col="Daten")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    geom_density(aes(col = "Kerndichteschätzer")) +
    stat_function(fun = dnorm, args = list(mean = mu, sd = sigma), aes(col = "NV, exakt")) +
    stat_function(fun = dnorm, args = list(mean = x.mean, sd = x.sd), aes(col = "NV, Daten")) +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3 * max.dens, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.9 * max.dens, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3 * max.dens, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.9 * max.dens, colour = "lightcyan", angle = 90) +
    labs(col = "Dichte")

  print(graph.pdf)

  graph.cdf <- ggplot(data = x.data, aes(x)) +
    stat_ecdf(aes(col = "empirische Verteilung")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    stat_function(fun = pnorm, args = list(mean = mu, sd = sigma), aes(col = "NV, exakt")) +
    stat_function(fun = pnorm, args = list(mean = mu, sd = sigma), aes(col = "NV, Daten")) +
    labs(col = "Verteilungsfunktion") +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

  print(graph.cdf)

  # return(list(graph.pdf, graph.cdf))
}

sim_normal(n = 100, mu = 3, sigma = 2)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

sim_normal(n = 10000, mu = 3, sigma = 2)

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

3 Diskrete Verteilungen

bei den diskreten Verteilungen stellen wir die relativen Häufigkeiten der Stichprobe gegen die Wahrscheinlichkeiten in Barplots dar, um die Wahrscheinlichkeitsfunktion zu veranschaulichen

3.1 Binomialverteilung

p <- 0.3
m <- 10 # bekannt

(exakt.mean <- m * p)

[1] 3

(exakt.var <- m * p * (1 - p))

[1] 2.1

(exakt.median <- qbinom(p = 0.5, size = m, prob = p))

[1] 3

# simulieren Daten nach Binomialverteilung
x <- rbinom(n = n, size = m, prob = p)
x.data <- tibble(x)

# empirische Masszahlen
(x.mean <- mean(x))

[1] 3.18

(x.median <- median(x))

[1] 3

(x.sd <- sd(x))

[1] 1.409733

(p.data <- x.mean / m)

[1] 0.318

# nur fuer Graphiken
d <- x.mean - x.median
d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

# absolute Hauefigkeiten
table(x)

x
 0  1  2  3  4  5  6  7 
 1  4 11 15 10  7  1  1 

# rel. Häufigkeiten
table(x) / length(x)

x
   0    1    2    3    4    5    6    7 
0.02 0.08 0.22 0.30 0.20 0.14 0.02 0.02 

# Wahrscheinlichkeiten
x.probs <- pbinom(q = 0:m, size = m, prob = p)
round(x.probs, digits = 3)

 [1] 0.028 0.149 0.383 0.650 0.850 0.953 0.989 0.998 1.000 1.000 1.000

Achtung: die Daten eines diskreten Merkmals sollte man nicht mehr in einem Histogramm darstellen, denn Groupierung der Daten macht hier keinen Sinn, wie die Graphiken auch zeigen…

ggplot(data = x.data, aes(x)) +
  geom_histogram(aes(y = after_stat(density))) +
  geom_density()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

etwas besser

ggplot(data = x.data, aes(x)) +
  geom_bar(aes(y = after_stat(prop))) +
  # geom_rug(col="gray") +  #add rug plot: Daten auf der X-Achse
  geom_density(aes(col = "Kerndichteschätzer"))

selbständige Berechnung der relativen Häufigkeiten und Wahrscheinlichkeiten und Darstellung als Barplot

x.emp <- x.data %>%
  group_by(x) %>%
  summarise(n = n()) %>%
  mutate(x.freq = n / sum(n))

x.data %>% table()

x
 0  1  2  3  4  5  6  7 
 1  4 11 15 10  7  1  1 

x.pdf <- dbinom(x = 0:m, size = m, prob = p)
# x.cdf = pbinom(q = 0:m, size = m, prob = p)

# x.exakt = tibble(x=0:m, x.pdf, x.cdf)
x.exakt <- tibble(x = 0:m, x.pdf)

x.all <- full_join(x.exakt, x.emp, by = "x")

x.all.long <- pivot_longer(x.all, cols = c(x.pdf, x.freq), values_to = "Prob", names_to = "type") %>%
  mutate(typ = recode_factor(type, x.pdf = "Modell", x.freq = "Daten")) %>%
  replace_na(list(Prob = 0))

print(x.all.long, n = 2 * (m + 1))

# A tibble: 22 × 5
       x     n type         Prob typ   
   <int> <int> <chr>       <dbl> <fct> 
 1     0     1 x.pdf  0.0282     Modell
 2     0     1 x.freq 0.02       Daten 
 3     1     4 x.pdf  0.121      Modell
 4     1     4 x.freq 0.08       Daten 
 5     2    11 x.pdf  0.233      Modell
 6     2    11 x.freq 0.22       Daten 
 7     3    15 x.pdf  0.267      Modell
 8     3    15 x.freq 0.3        Daten 
 9     4    10 x.pdf  0.200      Modell
10     4    10 x.freq 0.2        Daten 
11     5     7 x.pdf  0.103      Modell
12     5     7 x.freq 0.14       Daten 
13     6     1 x.pdf  0.0368     Modell
14     6     1 x.freq 0.02       Daten 
15     7     1 x.pdf  0.00900    Modell
16     7     1 x.freq 0.02       Daten 
17     8    NA x.pdf  0.00145    Modell
18     8    NA x.freq 0          Daten 
19     9    NA x.pdf  0.000138   Modell
20     9    NA x.freq 0          Daten 
21    10    NA x.pdf  0.00000590 Modell
22    10    NA x.freq 0          Daten 

Check: Summer der Wahrscheinlichkeiten ist jeweils 1

x.all.long %>%
  group_by(typ) %>%
  summarise(gesamt = sum(Prob))

# A tibble: 2 × 2
  typ    gesamt
  <fct>   <dbl>
1 Modell      1
2 Daten       1

ggplot(data = x.all.long, aes(x, y = Prob, fill = typ)) +
  geom_col() +
  facet_wrap(~type)

ggplot(data = x.all.long, aes(x, y = Prob, col = typ, fill = typ)) +
  geom_col(alpha = 0.2, position = "dodge") +
  labs(fill = NULL, col = NULL)

ggplot(data = x.all.long, aes(x, y = Prob, col = typ, fill = typ)) +
  geom_bar(stat = "identity", alpha = 0.2, position = "dodge") +
  labs(fill = NULL, col = NULL)

unabhängig ob diskrete oder stetige Merkmale: Darstellung der Verteilungsfunktion

ggplot(data = x.data, aes(x)) +
  stat_ecdf(aes(col = "empirische Verteilung")) +
  geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
  stat_function(fun = pbinom, args = list(size = m, prob = p), aes(col = "Bin, exakt"), n = 2000) +
  stat_function(fun = pbinom, args = list(size = m, prob = p.data), aes(col = "Bin, Daten"), n = 2000) +
  labs(col = "Verteilungsfunktion") +
  # empirischer Mittelwert:
  geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
  annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
  # exakter Mittelwert
  geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
  annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
  # empirischer Median
  geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
  annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
  # exakter Median
  geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
  annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

wieder als Funktion

sim_binomial <- function(n = 50, m = 10, p = 0.5) {
  exakt.mean <- m * p
  exakt.var <- m * p * (1 - p)
  exakt.median <- qbinom(p = 0.5, size = m, prob = p)

  # simulieren Daten nach Binomialverteilung
  x <- rbinom(n = n, size = m, prob = p)
  x.data <- tibble(x)

  # empirische Masszahlen
  x.mean <- mean(x)
  x.median <- median(x)
  x.sd <- sd(x)

  p.data <- x.mean / m

  # nur fuer Graphiken
  d <- x.mean - x.median
  d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
  d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

  x.emp <- x.data %>%
    group_by(x) %>%
    summarise(n = n()) %>%
    mutate(x.freq = n / sum(n))

  # x.data %>% table()

  x.pdf <- dbinom(x = 0:m, size = m, prob = p)
  x.exakt <- tibble(x = 0:m, x.pdf)
  x.all <- full_join(x.exakt, x.emp, by = "x")

  x.all.long <- pivot_longer(x.all, cols = c(x.pdf, x.freq), values_to = "Prob", names_to = "type") %>%
    mutate(typ = recode_factor(type, x.pdf = "Modell", x.freq = "Daten")) %>%
    replace_na(list(Prob = 0))


  graph.pdf <- ggplot(data = x.all.long, aes(x, y = Prob, col = typ, fill = typ)) +
    geom_bar(stat = "identity", position = "dodge") +
    labs(fill = NULL, col = NULL)

  graph.cdf <- ggplot(data = x.data, aes(x)) +
    stat_ecdf(aes(col = "empirische Verteilung")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    stat_function(fun = pbinom, args = list(size = m, prob = p), aes(col = "Bin, exakt"), n = 2000) +
    stat_function(fun = pbinom, args = list(size = m, prob = p.data), aes(col = "Bin, Daten"), n = 2000) +
    labs(col = "Verteilungsfunktion") +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

  print(graph.pdf)
  print(graph.cdf)
  # return(list(graph.pdf,graph.cdf))
}

sim_binomial(n = 100, m = 10, p = 0.3)

sim_binomial(n = 10000, m = 10, p = 0.5)

3.2 Hypergeometrische Verteilung

sim_hyper <- function(n = 50, White = 10, Black = 10, k = 10) {
  # X = number white balls by k x drawing without replacement
  p <- White / (White + Black)
  exakt.mean <- k * p

  exakt.var <- k * p * (1 - p) * (White + Black - k) / (White + Black - 1)
  exakt.median <- qhyper(p = 0.5, m = White, n = Black, k = k)

  # simulieren Daten nach Binomialverteilung
  x <- rhyper(nn = n, m = White, n = Black, k = k)
  x.data <- tibble(x)

  # empirische Masszahlen
  x.mean <- mean(x)
  x.median <- median(x)
  x.sd <- sd(x)



  # nur fuer Graphiken
  d <- x.mean - x.median
  d.mean <- -0.2 * (d < 0) + 0.2 * (d >= 0)
  d.median <- 0.2 * (d < 0) - 0.2 * (d >= 0)

  x.emp <- x.data %>%
    group_by(x) %>%
    summarise(n = n()) %>%
    mutate(x.freq = n / sum(n))

  # x.data %>% table()

  x.pdf <- dhyper(x = 0:k, m = White, n = Black, k = k)
  x.exakt <- tibble(x = 0:k, x.pdf)
  x.all <- full_join(x.exakt, x.emp, by = "x")

  x.all.long <- pivot_longer(x.all, cols = c(x.pdf, x.freq), values_to = "Prob", names_to = "type") %>%
    mutate(typ = recode_factor(type, x.pdf = "Modell", x.freq = "Daten")) %>%
    replace_na(list(Prob = 0))


  graph.pdf <- ggplot(data = x.all.long, aes(x, y = Prob, col = typ, fill = typ)) +
    geom_bar(stat = "identity", position = "dodge") +
    labs(fill = NULL, col = NULL)

  graph.cdf <- ggplot(data = x.data, aes(x)) +
    stat_ecdf(aes(col = "empirische Verteilung")) +
    geom_rug(col = "gray") + # add rug plot: Daten auf der X-Achse
    stat_function(fun = phyper, args = list(m = White, n = Black, k = k), aes(col = "Hyp, exakt"), n = 2000) +
    stat_function(fun = phyper, args = list(m = White, n = Black, k = k), aes(col = "Hyp, Daten"), n = 2000) +
    labs(col = "Verteilungsfunktion") +
    # empirischer Mittelwert:
    geom_vline(aes(xintercept = x.mean), linetype = "dashed", linewidth = 1, colour = "green") +
    annotate("text", label = "emp. Mean", x = x.mean + d.mean * x.sd, y = 0.3, colour = "green", angle = 90) +
    # exakter Mittelwert
    geom_vline(aes(xintercept = exakt.mean), linetype = "dotted", linewidth = 0.5, colour = "lightgreen") +
    annotate("text", label = "exakt", x = exakt.mean + d.mean * sqrt(exakt.var), y = 0.8, colour = "lightgreen", angle = 90) +
    # empirischer Median
    geom_vline(aes(xintercept = x.median), linetype = "dashed", linewidth = 1, colour = "cyan") +
    annotate("text", label = "emp. Median", x = x.median + d.median * x.sd, y = 0.3, colour = "cyan", angle = 90) +
    # exakter Median
    geom_vline(aes(xintercept = exakt.median), linetype = "dotted", linewidth = 1, colour = "lightcyan") +
    annotate("text", label = "exakt", x = exakt.median + d.median * sqrt(exakt.var), y = 0.8, colour = "lightcyan", angle = 90)

  print(graph.pdf)
  print(graph.cdf)
  # return(list(graph.pdf,graph.cdf))
}

sim_hyper(n = 100, White = 100, Black = 50, k = 20)

sim_hyper(n = 1000, White = 100, Black = 50, k = 20)