4. Visualisierung mit Matplotlib#
Matplotlib ist eine mächtige Python-Bibliothek, welche viele Funktionen für die graphische Darstellung in Form von Plots und Diagrammen bereitstellt. Wir werden in diesem Abschnitt die grundlegende Funktionsweise kennenlernen.
4.1. Erste Schritte#
Ähnlich wie bei NumPy müssen wir Matplotlib erst installieren. Dies erledigt man in seiner Conda-Umgebung mit folgendem Befehl:
conda install -c conda-forge matplotlib
Anschließend können wir Matplotlib, besser gesagt das Submodul matplotlib.pyplot in unser Programm einbinden:
import matplotlib.pyplot as plt
Der wichtigste Befehl ist plt.plot(...). Wir geben plt.plot? ein um zu erfahren wie dieser funktioniert. In der einfachsten Form sind die Argumente dieser Funktion 2 Vektoren mit \(x\)- bzw. \(y\)-Koordinaten einer Punktwolke. Diese Vektoren können Listen, oder Numpy-Arrays sein. Die Sinusfunktion können wir wie folgt plotten:
import numpy as np
x = np.linspace(0, 2*np.pi, 11) # Erzeuge Gitter [0, 0.2*pi, 0.4*pi, ..., 2*pi])
y = np.sin(x) # Berechne zugehörige Funktionswerte
plt.plot(x,y) # Erzeuge Plot
plt.show() # Zeige den Plot
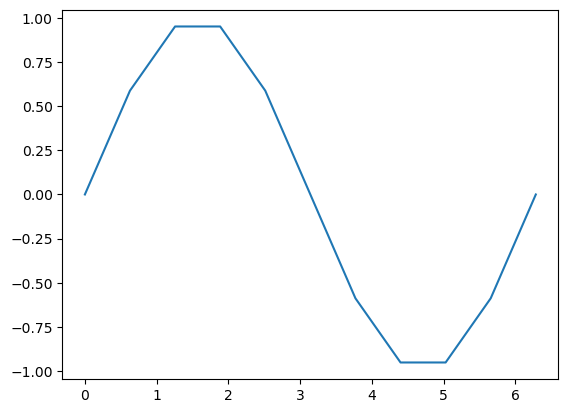
Hier sehen wir auch eine schöne Anwendung der komponentenweise definierten mathematischen Funktionen aus numpy.
Übungsaufgabe
Plotte die Funktion \(f(x) = e^{-x}\,\sin(2\,\pi\,x)\) im Intervall \([0,6]\).
4.2. Gestaltung von Plots#
Machen wir unseren Plot noch etwas schöner:
import numpy as np
x = np.linspace(0,4*np.pi, 1001) # Erzeuge äquidistantes Gitter für das Intervall [0, 4*pi]
y = np.sin(x) # Berechne zugehörige Funktionswerte für sinus
z = np.cos(x) # und cosinus
plt.figure(figsize=(10,5)) # Größe einstellen
plt.plot(x,y,label="$\sin(x)$") # Erzeuge Plot für Sinus
plt.plot(x,z,label="$\cos(x)$") # Erzeuge Plot für Cosinus
plt.title("Sinus und Cosinus") # Titel des Plots
plt.grid() # Gitterlinien einschalten
plt.xlabel('x') # Bezeichner an x-Achse
plt.ylabel('f(x)') # Bezeichner an y-Achse (in Latex-Code)
plt.legend() # Legende
plt.show() # Zeige den Plot
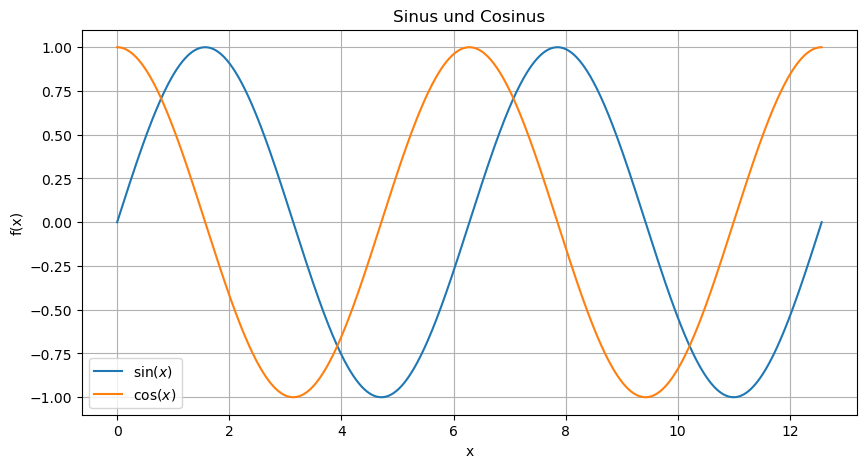
Im Prinzip hat Matplotlib unsere Punktwolke mit Koordinaten aus x und y gezeichnet, und die Punkte mit Linen verbunden. Es gibt aber noch einige andere Linientypen:
x = np.linspace(0,2,21)
y1= x-0.5*x**2
y2= 2*x-x**2
y3= 3*x-1.5*x**2
plt.figure(figsize=(10,5)) # Größe einstellen
# Zeichne rote (r) Kreise (o) mit Verbindungslinien (-)
plt.plot(x, y1, 'ro-', linewidth=0.2, label='f1')
# Zeichne blaue (b) Quadrate (s)
plt.plot(x, y2, 'bs', label='f1')
# Zeichne cyane (c) Dreiecke (^) mit gestrichelten Verbindungslinien (--)
plt.plot(x, y3, 'c^--', markersize=10, label='f1')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()
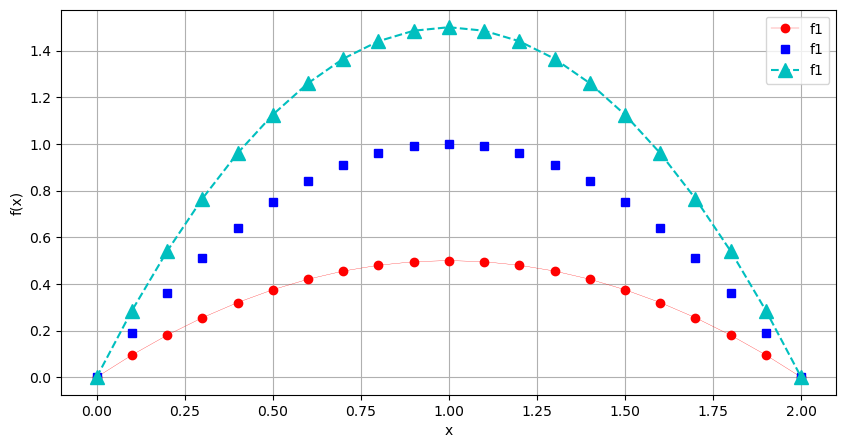
Im Hilfetext plt.plot? sind noch weitere Linien- und Markertypen erklärt. Vordefinierte Farben im Submodul matplotlib.colors. Es gibt verschiedene Farbpaletten. Die Grundfarben sind:
import matplotlib.colors as mcolors
mcolors.BASE_COLORS
{'b': (0, 0, 1),
'g': (0, 0.5, 0),
'r': (1, 0, 0),
'c': (0, 0.75, 0.75),
'm': (0.75, 0, 0.75),
'y': (0.75, 0.75, 0),
'k': (0, 0, 0),
'w': (1, 1, 1)}
Es gibt weiterhin die Farbpalette Tableau:
mcolors.TABLEAU_COLORS
{'tab:blue': '#1f77b4',
'tab:orange': '#ff7f0e',
'tab:green': '#2ca02c',
'tab:red': '#d62728',
'tab:purple': '#9467bd',
'tab:brown': '#8c564b',
'tab:pink': '#e377c2',
'tab:gray': '#7f7f7f',
'tab:olive': '#bcbd22',
'tab:cyan': '#17becf'}
Und außerdem noch CSS-Farben:
mcolors.CSS4_COLORS
{'aliceblue': '#F0F8FF',
'antiquewhite': '#FAEBD7',
'aqua': '#00FFFF',
'aquamarine': '#7FFFD4',
'azure': '#F0FFFF',
'beige': '#F5F5DC',
'bisque': '#FFE4C4',
'black': '#000000',
'blanchedalmond': '#FFEBCD',
'blue': '#0000FF',
'blueviolet': '#8A2BE2',
'brown': '#A52A2A',
'burlywood': '#DEB887',
'cadetblue': '#5F9EA0',
'chartreuse': '#7FFF00',
'chocolate': '#D2691E',
'coral': '#FF7F50',
'cornflowerblue': '#6495ED',
'cornsilk': '#FFF8DC',
'crimson': '#DC143C',
'cyan': '#00FFFF',
'darkblue': '#00008B',
'darkcyan': '#008B8B',
'darkgoldenrod': '#B8860B',
'darkgray': '#A9A9A9',
'darkgreen': '#006400',
'darkgrey': '#A9A9A9',
'darkkhaki': '#BDB76B',
'darkmagenta': '#8B008B',
'darkolivegreen': '#556B2F',
'darkorange': '#FF8C00',
'darkorchid': '#9932CC',
'darkred': '#8B0000',
'darksalmon': '#E9967A',
'darkseagreen': '#8FBC8F',
'darkslateblue': '#483D8B',
'darkslategray': '#2F4F4F',
'darkslategrey': '#2F4F4F',
'darkturquoise': '#00CED1',
'darkviolet': '#9400D3',
'deeppink': '#FF1493',
'deepskyblue': '#00BFFF',
'dimgray': '#696969',
'dimgrey': '#696969',
'dodgerblue': '#1E90FF',
'firebrick': '#B22222',
'floralwhite': '#FFFAF0',
'forestgreen': '#228B22',
'fuchsia': '#FF00FF',
'gainsboro': '#DCDCDC',
'ghostwhite': '#F8F8FF',
'gold': '#FFD700',
'goldenrod': '#DAA520',
'gray': '#808080',
'green': '#008000',
'greenyellow': '#ADFF2F',
'grey': '#808080',
'honeydew': '#F0FFF0',
'hotpink': '#FF69B4',
'indianred': '#CD5C5C',
'indigo': '#4B0082',
'ivory': '#FFFFF0',
'khaki': '#F0E68C',
'lavender': '#E6E6FA',
'lavenderblush': '#FFF0F5',
'lawngreen': '#7CFC00',
'lemonchiffon': '#FFFACD',
'lightblue': '#ADD8E6',
'lightcoral': '#F08080',
'lightcyan': '#E0FFFF',
'lightgoldenrodyellow': '#FAFAD2',
'lightgray': '#D3D3D3',
'lightgreen': '#90EE90',
'lightgrey': '#D3D3D3',
'lightpink': '#FFB6C1',
'lightsalmon': '#FFA07A',
'lightseagreen': '#20B2AA',
'lightskyblue': '#87CEFA',
'lightslategray': '#778899',
'lightslategrey': '#778899',
'lightsteelblue': '#B0C4DE',
'lightyellow': '#FFFFE0',
'lime': '#00FF00',
'limegreen': '#32CD32',
'linen': '#FAF0E6',
'magenta': '#FF00FF',
'maroon': '#800000',
'mediumaquamarine': '#66CDAA',
'mediumblue': '#0000CD',
'mediumorchid': '#BA55D3',
'mediumpurple': '#9370DB',
'mediumseagreen': '#3CB371',
'mediumslateblue': '#7B68EE',
'mediumspringgreen': '#00FA9A',
'mediumturquoise': '#48D1CC',
'mediumvioletred': '#C71585',
'midnightblue': '#191970',
'mintcream': '#F5FFFA',
'mistyrose': '#FFE4E1',
'moccasin': '#FFE4B5',
'navajowhite': '#FFDEAD',
'navy': '#000080',
'oldlace': '#FDF5E6',
'olive': '#808000',
'olivedrab': '#6B8E23',
'orange': '#FFA500',
'orangered': '#FF4500',
'orchid': '#DA70D6',
'palegoldenrod': '#EEE8AA',
'palegreen': '#98FB98',
'paleturquoise': '#AFEEEE',
'palevioletred': '#DB7093',
'papayawhip': '#FFEFD5',
'peachpuff': '#FFDAB9',
'peru': '#CD853F',
'pink': '#FFC0CB',
'plum': '#DDA0DD',
'powderblue': '#B0E0E6',
'purple': '#800080',
'rebeccapurple': '#663399',
'red': '#FF0000',
'rosybrown': '#BC8F8F',
'royalblue': '#4169E1',
'saddlebrown': '#8B4513',
'salmon': '#FA8072',
'sandybrown': '#F4A460',
'seagreen': '#2E8B57',
'seashell': '#FFF5EE',
'sienna': '#A0522D',
'silver': '#C0C0C0',
'skyblue': '#87CEEB',
'slateblue': '#6A5ACD',
'slategray': '#708090',
'slategrey': '#708090',
'snow': '#FFFAFA',
'springgreen': '#00FF7F',
'steelblue': '#4682B4',
'tan': '#D2B48C',
'teal': '#008080',
'thistle': '#D8BFD8',
'tomato': '#FF6347',
'turquoise': '#40E0D0',
'violet': '#EE82EE',
'wheat': '#F5DEB3',
'white': '#FFFFFF',
'whitesmoke': '#F5F5F5',
'yellow': '#FFFF00',
'yellowgreen': '#9ACD32'}
Durch Setzen des Parameters color im Plot-Befehl kann nun eine Farbe aus einer der oberen Farbpaletten gewählt werden:
x = np.linspace(0,1,10)
plt.plot(x,0.5*x*(1-x),'o-',color='g') # Grundfarbe
plt.plot(x,x*(1-x),'d-',color='tab:olive') # Tableau-Farbe
plt.plot(x,1.5*x*(1-x),'s-',color='firebrick') # CSS-Farbe
plt.show()
Show code cell source
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_colortable(colors, title, sort_colors=True, emptycols=0):
cell_width = 212
cell_height = 22
swatch_width = 48
margin = 12
topmargin = 40
# Sort colors by hue, saturation, value and name.
if sort_colors is True:
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgb(color))),
name)
for name, color in colors.items())
names = [name for hsv, name in by_hsv]
else:
names = list(colors)
n = len(names)
ncols = 4 - emptycols
nrows = n // ncols + int(n % ncols > 0)
width = cell_width * 4 + 2 * margin
height = cell_height * nrows + margin + topmargin
dpi = 72
fig, ax = plt.subplots(figsize=(width / dpi, height / dpi), dpi=dpi)
fig.subplots_adjust(margin/width, margin/height,
(width-margin)/width, (height-topmargin)/height)
ax.set_xlim(0, cell_width * 4)
ax.set_ylim(cell_height * (nrows-0.5), -cell_height/2.)
ax.yaxis.set_visible(False)
ax.xaxis.set_visible(False)
ax.set_axis_off()
ax.set_title(title, fontsize=24, loc="left", pad=10)
for i, name in enumerate(names):
row = i % nrows
col = i // nrows
y = row * cell_height
swatch_start_x = cell_width * col
text_pos_x = cell_width * col + swatch_width + 7
ax.text(text_pos_x, y, name, fontsize=14,
horizontalalignment='left',
verticalalignment='center')
ax.add_patch(
Rectangle(xy=(swatch_start_x, y-9), width=swatch_width,
height=18, facecolor=colors[name], edgecolor='0.7')
)
return fig
plot_colortable(mcolors.BASE_COLORS, "Grundfarben",
sort_colors=False, emptycols=1)
plot_colortable(mcolors.TABLEAU_COLORS, "Tableau-Palette",
sort_colors=False, emptycols=2)
plot_colortable(mcolors.CSS4_COLORS, "CSS-Farben")
# Optionally plot the XKCD colors (Caution: will produce large figure)
# xkcd_fig = plot_colortable(mcolors.XKCD_COLORS, "XKCD Colors")
# xkcd_fig.savefig("XKCD_Colors.png")
plt.show()
Bei der Fehleranalyse sind oft logarithmische Achsen von interesse. Angenommen, wir analysieren einen iterativen Algorithmus und messen die Entfernung \(\text{err}_n\) zwischen exakter Lösung und der berechnete Näherungslösung nach \(n\) Iterationen. Man sagt, das Verfahren konvergiert
Q-linear, falls \(\text{err}_n \le C\, \text{err}_{n-1}\) mit \(C\in (0,1)\)
Q-superlinear, falls \(\text{err}_n \le \varepsilon_n\,\text{err}_{n-1}\) mit einer Nullfolge \(\varepsilon_n\searrow 0\)
Q-quadratisch, falls \(\text{err}_n \le C\, \text{err}_{n-1}^2\) mit \(C>0\).
Stellen wir den Fehlerverlauf in einem kartesischen Koordinatensystem und einem Koordinatensystem mit logarithmischer \(y\)-Achse dar:
import math
n = np.array(range(1,6), dtype='float64')
err_p1 = (0.8)**n
err_p2 = [1./math.factorial(int(i)) for i in n]
err_p3 = (0.8)**(2**n)
plt.figure(figsize=(10,5))
def generate_plot():
plt.plot(n, err_p1, 'ro-', label='Q-linear')
plt.plot(n, err_p2, 'bo-', label='Q-superlinear')
plt.plot(n, err_p3, 'co-', label='Q-quadratisch')
plt.grid()
# Plot in kartesischen Koordinatensystem
plt.subplot(1,2,1)
generate_plot()
plt.legend(loc='upper right')
# Plot in Koordinatensystem mit logarithmischer y-Achse
plt.subplot(1,2,2)
generate_plot()
plt.semilogy()
plt.legend(loc='lower left')
plt.show()
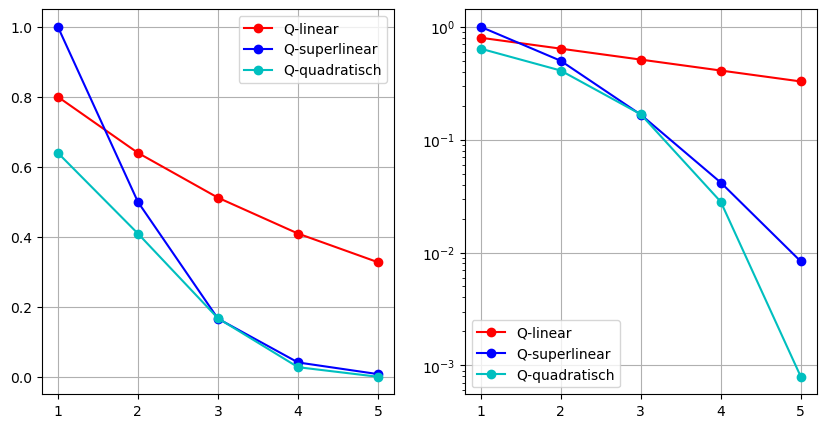
Wir sehen, dass eine \(Q\)-linear konvergente Folge im Plot mit logarithmischer \(y\)-Achse einer lineare Funktion ist.
Analog dazu kann man auch die \(x\)-Achse mit plt.semilogx() logatithmisch skalieren, was bei oben vorgestellter Anwendung allerdings wenig Sinn macht.
4.3. Balken-, Linien- und Kuchendiagramme#
Schauen wir uns weitere elementare Plot-Typen an. Angenommen wir haben die Auswertung einer Umfrage vorliegen, und möchten diese graphisch aufbereiten. Unsere Beispieldaten sind:
parties = ["CDU", "SPD", "FDP", "Grüne", "Linke", "AfD", "Sonstige"]
colors = ["black", "red", "yellow", "green", "violet", "blue", "gray"]
values = [25.3, 26.3, 13.9, 14.2, 6.2, 4.9]
values.append(100-sum(values))
Wir können anstelle des plot-Befehls auch stem verwenden um ein Liniendiagramm zu erstellen, scatter für ein Streudiagramm, bar für ein Balkendiagramm oder pie für ein Tortendiagramm. Im folgenden Beispiel werden die Unterschiede gezeigt:
plt.figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.stem(parties, values)
plt.title("Plot")
plt.subplot(2,2,2)
plt.bar(parties, values, color=colors)
plt.title("Bar")
plt.subplot(2,2,3)
plt.scatter(parties, values, color=colors)
plt.title("Scatter")
plt.subplot(2,2,4)
plt.pie(values, labels=parties, explode=[0,0.2,0,0.2,0,0,0], colors=colors)
plt.title("Pie")
plt.show()
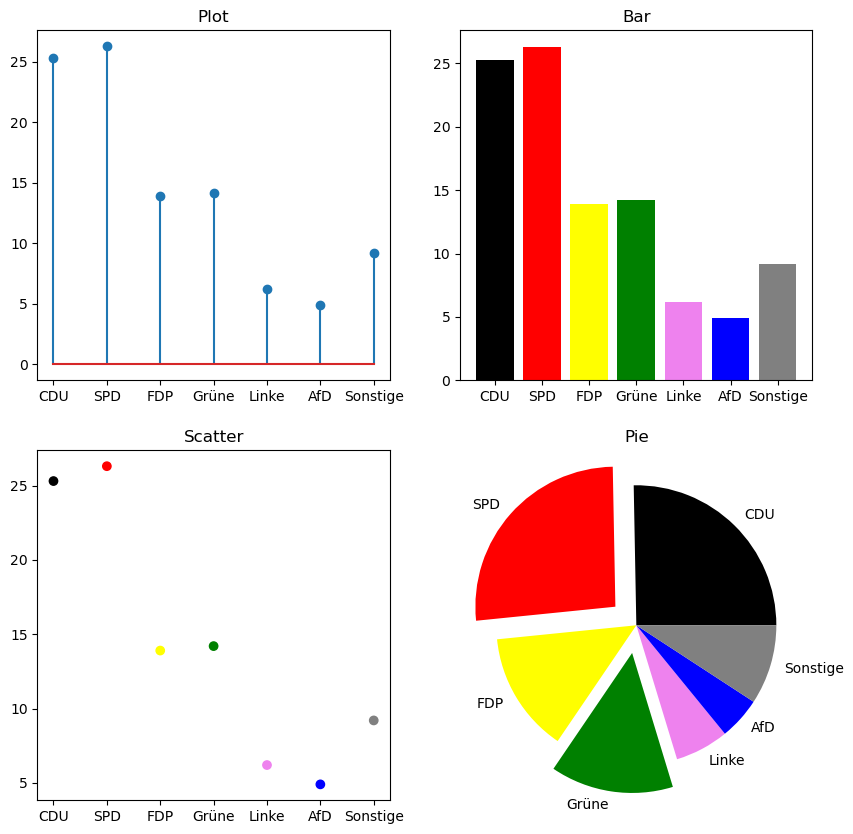
4.4. Plots für Skalar- und Vektorfelder#
Auch für die graphische Darstellung von Skalarfeldern \(f\colon \mathbb{R}^2 \to \mathbb{R}\) und Vektorfeldern \(\vec F\colon \mathbb{R}^2 \to \mathbb{R}^2\) stehen einige Funktionen in Matplotlib bereit. Die meisten Funktionen zur Darstellung von Skalarfeldern erwarten als Argument 3 Matrizen, eine für die \(x\)-Koordinaten, eine für die \(y\)-Koordinaten und eine für den Funktionswert \(f(x,y)\). Hilfreich ist hier die Funktion numpy.meshgrid mit der wir ein 2D-Tensorprodukt-Gitter aus 2 1D-Gittern erzeugen:
# 1D-Gitter für x- und y-Variable
x = np.linspace(-4.5,3.5,1001)
y = np.linspace(-3.5,3.5,1001)
# 2D-Gitter erzeugen
X,Y = np.meshgrid(x,y)
# Definiere Himmelblau-Funktion
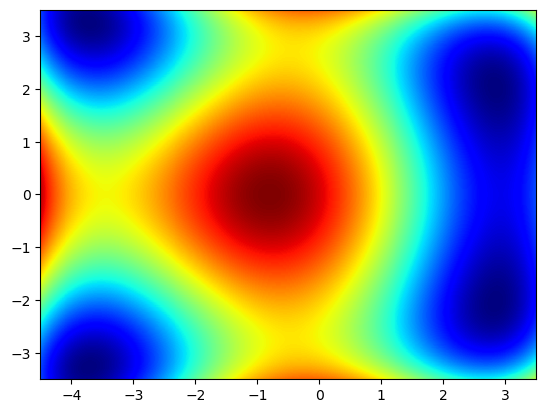
Z = (X**2 + y - 11)**2 + (X + Y**2 - 7)**2
Eine mögliche Darstellung einer solchen Funktion wäre ein Contour-Plot, in welchem die Kurven \(\{(x,y)\colon f(x,y)=c_i\}\) für verschiedene Werte \(c_1<c_2 < \ldots<c_{\text{levels}}\) eingezeichnet werden:
plt.contour(X,Y,Z, levels=25)
plt.colorbar()
plt.show()
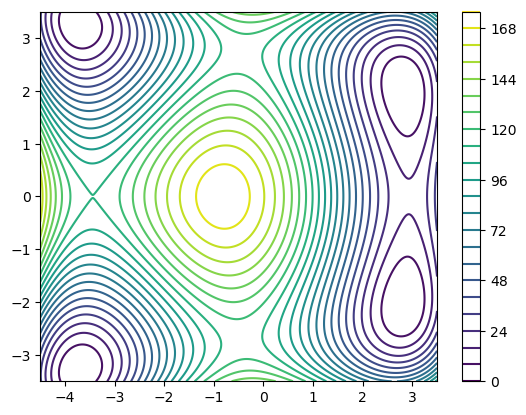
Ähnlich funktionieren Color-Plots, bei denen der Funktionswert an einer Stelle \((x,y)\) dem Farbwert einer vordefinierten Farbpalette entspricht:
import matplotlib.cm as cm
plt.pcolormesh(X,Y,Z, cmap=cm.jet)
plt.show()
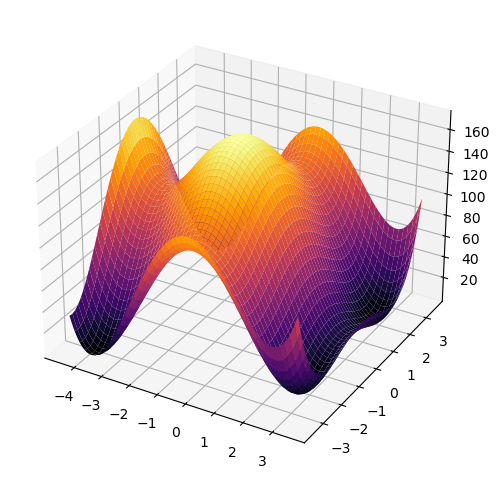
Skalarfelder lassen sich auch in dreidimensionalen Koordinatensystemen darstellen. Die Argumente werden auf \(x\)- und \(y\)-Achse aufgetragen, und der Funktionswert auf die \(z\)-Achse. Die entsprechenden Plot-Befehle sind allerdings nicht im Submodul matplotlib.pyplot definiert, daher müssen wir einen Umweg nehmen. Zunächst erzeugen wir uns ein Bildobjekt mit
fig = plt.figure()
fügen ein 3D-Koordinatensystem hinzu
ax = fig.axes(projection='3d')
und nutzen die vom Objekt ax bereitgestellten Plot-Befehle. Hier ein Beispiel:
plt.figure(figsize=(8,6))
# 3D-Koordinatensystem hinzufügen
ax = plt.axes(projection='3d')
# Surface-Plot erstellen
ax.plot_surface(X,Y,Z, cmap=cm.inferno)
plt.show()
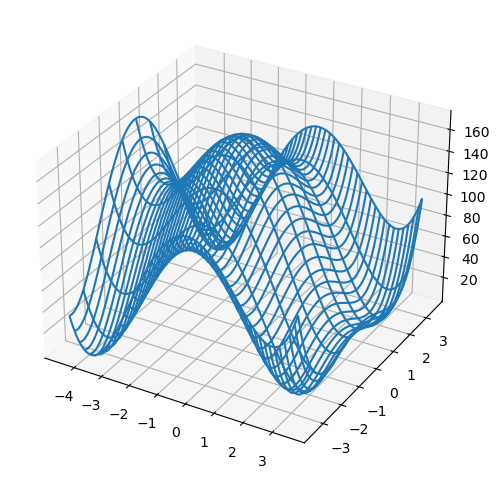
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z, rcount=10)
plt.show()
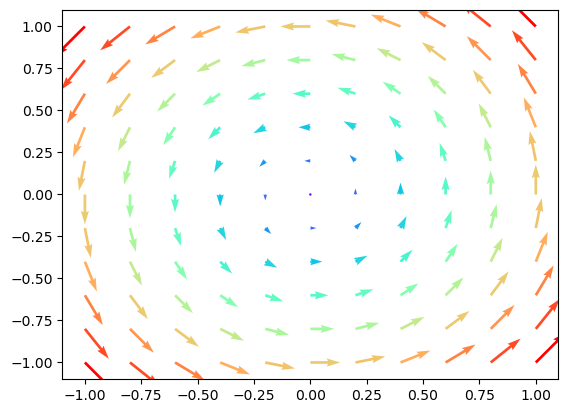
Schauen wir uns noch eine Methode mit der wir Vektorfelder zeichnen können. Als Beispiel definieren wir \(\vec f(x,y) = (-y,x)^\top\). Solche Vektorfelder können in sogenannten Quiver-Plots dargestellt werden:
x = np.linspace(-1,1, 11)
y = np.linspace(-1,1, 11)
# Punktgitter definieren
X,Y = np.meshgrid(x, y)
# Funktionswerte von F
Z1 = -Y
Z2 = X
# Optional: Färbe Pfeile nach Länge
C = np.sqrt(Z1**2 + Z2**2)
# Quiverplot erzeugen und anzeigen
plt.quiver(X, Y, Z1, Z2, C, cmap=cm.rainbow)
plt.show()
Auch Kurven lassen sich in Matplotlib zeichnen. Eine Kurve ist zunächst eine Menge an Punkten
mit einer sogenannten Kurvenparametrisierung \(\vec x\colon[t_a,t_b]\to\mathbb{R}^n\), welche regulär ist, d.h., \(\dot{\vec x}(t)\ne 0\) für alle \(t\in [t_a,t_b]\). Für eine ebene Kurve (\(n=2\)) können wir den normalen Plot-Befehl nutzen. Das Kleeblatt
zeichnen wir beispielsweise mit
t = np.linspace(0,2*np.pi,100)
x = np.cos(t)+np.cos(2*t)
y = np.sin(t)-np.sin(2*t)
plt.plot(x,y,'o-')
plt.grid()
plt.show()
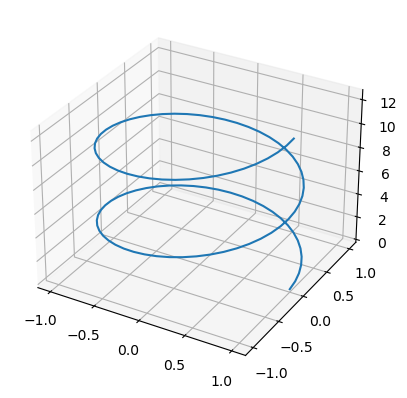
Ähnlich kann man Raumkurven (\(n=3\)) zeichnen, man benötigt nur vorher ein dreidimensionales Koordinatensystem. Wie wir das anlegen haben wir aber schon gesehen. Wir zeichnen hier die Schraubenlinie
t = np.linspace(0,4*np.pi,100)
x = np.cos(t)
y = np.sin(t)
z = t
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z)
plt.show()
