Momentanpolermittlung
Polygonmethode
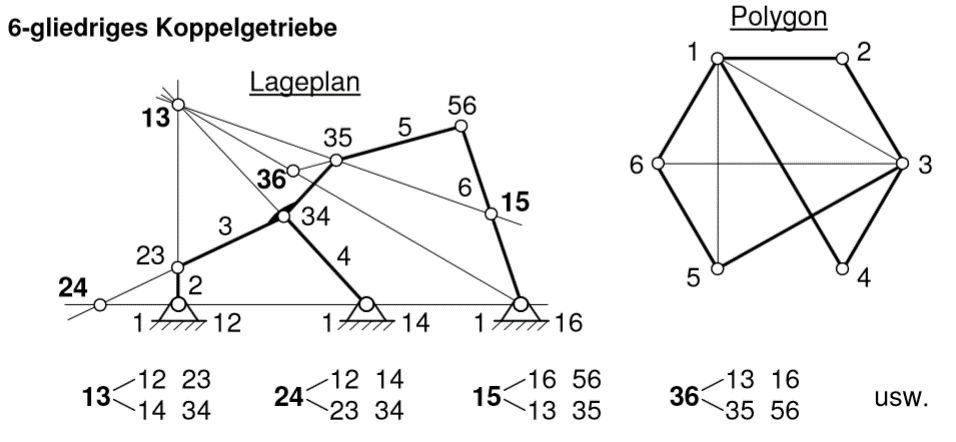
- Bezeichnung aller Getriebeglieder im Lageplan (Getriebeglied 1 ist stets das Gestell).
- Zeichnen des Polygons, wobei jeder Eckpunkt einem Getriebeglied entspricht.
- Kennzeichnen der vorhandenen Momentanpole (Strukturpole/ Gelenke) durch stark gezeichnete Verbindungslinien der Polygonpunkte.
- Markieren der gesuchten Momentanpole in der Polkonfiguration.
- Nach dem Theorem von Aronhold/Kennedy (Satz von den drei Momentanpolen) ergibt sich der gesuchte Momentanpol als Schnittpunkt zweier Polgeraden, einer Polgeraden und einer Kurvengelenknormalen oder zweier Kurvengelenknormalen. Diese Polgeraden können im Lageplan eingezeichnet werden, wenn im Polygon über der dem gesuchten Momentanpol entsprechenden Polygonseite zwei Dreiecke vorhanden sind.
Für die Anzahl der Pole in einem n-gliedrigen Getriebe gilt:
\(z={n\choose 2}= \frac{n}{2}(n-1)\)
Alle Pole füllen eine Polmatrix. Pole mit gleichen Indexziffern sind identisch und Pole mit identischen Indexziffern existieren nicht.
\begin{matrix}
12 & 13 & 14\\
& 23 & 24\\
& & 34
\end{matrix}
Immer die kleinste Zahl zuerst:
\(Q_{12}\) = \(Q_{21}\) = \(12\)
Eine Schiebung gilt als Sonderfall einer Drehung mit unendlich fernem Pol \(𝑋𝑌_∞\), wobei jede zu ihm führende Gerade senkrecht auf der Schubrichtung steht.
Schnittpunkt zweier Polgeraden
Schnittpunkt Polgerade und Kurvengelenknormale
Satz von den drei Momentanpolen/ Theorem von Aronhold/ Kennedy
Die bei der Bewegung dreier Ebenen auftretenden 3 Momentanpole liegen auf einer Geraden.