Gelenke und Gelenkfreiheiten
Gelenke
Ein Gelenk ist die bewegliche Verbindungsstelle zweier Getriebeglieder. Es hat die Aufgabe, die dauernde gegenseitige Berührung der Getriebeglieder unter Gewährleistung ihrer relativen Beweglichkeit zu sichern. Es besteht aus 2 Gelenkelementen, die eine zueinander passende (zweckvolle) geometrische Formen haben müssen. (Bsp.: Zapfen – Lagerschale; 2 Zahnräder)
Gelenke können nach der Berührungsart sowie anhand ihres Gelenkfreiheitsgrades \(f\) unterschieden werden. Dies führt zu folgenden Möglichkeiten:
- Punktkontakt: z.B. Kugel/Ebene
- Linienkontakt: z.B. Zylinder/Ebene
- Flächenkontakt: z.B. Ebene/Ebene
Punktkontakt
Linienkontakt
FlächenkontaktWeitere Möglichkeiten zur Unterscheidung der Gelenke sind folgende:
- Form der Relativbewegung der miteinander verbundenen Glieder: z.B. Drehen, Schieben, Schrauben und deren Kombination
- Art der Paarung der Gelenkelemente: z. B. Kraft- oder Formschluss
- Bewegungsverhalten an der Kontaktstelle: z.B. Gleiten, Wälzen und deren Kombination
Das Bewegungsverhalten sowie die Art der Berührung der Gelenkelemente an der Kontaktstelle haben einen entscheidenden Einfluss auf die Beanspruchung und den Verschleiß der Gelenke.
Gelenkfreiheitsgrad und Unfreiheiten
Gelenkfreiheitsgrad
Der Gelenkfreiheitsgrad \(f\) ist die Anzahl der unabhängig voneinander möglichen Einzelbewegungen (Freiheiten oder Elementarbewegungen) der beiden Gelenkelemente bzw.
die Anzahl der vorhandenen Drehachsen eines Gelenks. In einem rechtwinkligen Bezugssystem sind als Einzelbewegungen 3 Drehungen \(D\) und 3 Schiebungen \(S\) möglich.
\[ f=S+D\]
Der räumliche Gelenkfreiheitsgrad ist: \(1 \leq f \leq 5\). Ein Gelenkfreiheitsgrad von \(f=0\) entspricht einer festen Verbindung und bei einem Gelenkfreiheitsgrad von \(f=6\) tritt kein Gelenkkontakt auf.
Beispiele: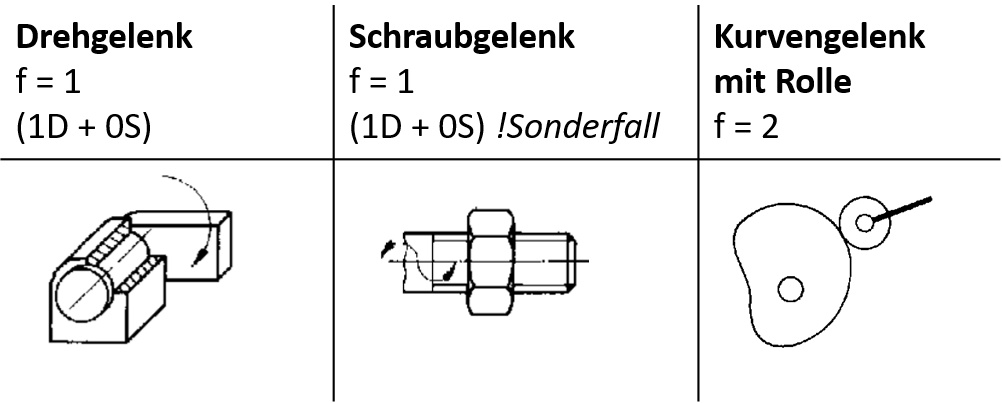 
Unfreiheiten
Die durch das Gelenk verhinderten Einzelbewegungen werden als Unfreiheiten \(u\) bezeichnet. Ihre Anzahl ist für den allgemein rämlichen Fall: \(u = 6 - f\).
Bewegungsgrad
Der Bewegungsgrad \(b\) entspricht der max. möglichen Anzahl der Einzelbewegungen eines Getriebegliedes: \(b = f + u\). Für ebene Bewegungen ist daher der Bewegungsgrad \(b = 3\), für räumliche Bewegungen gilt \(b = 6\).
Überbestimmung
Der Grad der Überbestimmung \(ü\) bei Gelenken entspricht der Anzahl der notwendigen Lagetoleranzen und ergibt sich aus: \[ü=6(k-1) + f - \sum_{i=1}^k f_i\]
\(k\) = Anzahl der Kontaktstellen (Punkt-, Linien- oder Flächenkontakt)
\(f\) = Gelenkfreiheitsgrad des Gelenkes- oder Gelenkverbandes
\(f_i\) = Teilgelenkfreiheitsgrad an der freigeschnittenen Kontaktstelle
Drehungen \(D=3\); Schiebungen \(S=2\)
Gelenkfreiheitsgrad \(f=5\)
Anzahl Kontaktstellen \(k=1\)
Freiheitsgrade an den Kontaktstellen \(f_{id}=5\)
Überbestimmung \(ü=0\)
Drehungen \(D=3\); Schiebungen \(S=2\)
Gelenkfreiheitsgrad \(f=5\)
Anzahl Kontaktstellen \(k=2\)
Freiheitsgrade an den Kontaktstellen \(f_{id}=5\)
Überbestimmung \(ü=1\) \(\rightarrow\) Der Durchmesser der Kugel muss toleriert werden