3 Lagen einer Ebene E in einer Bezugebene \(E_0\)
Grundlagen
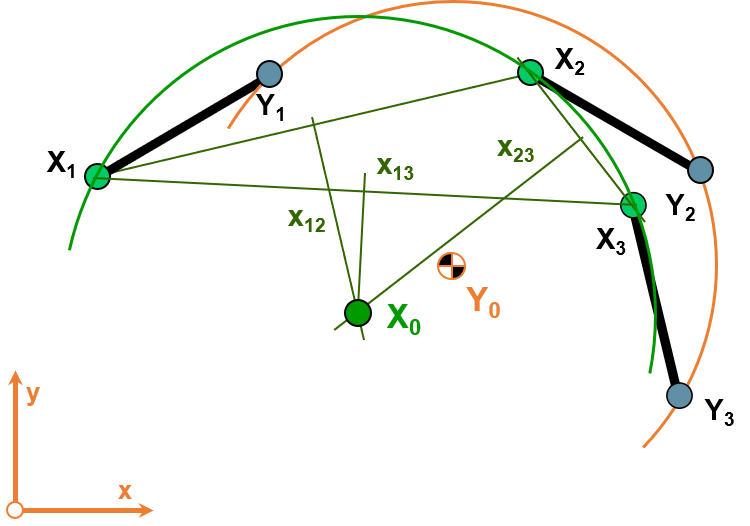
Eine Ebene E – gekennzeichnet durch die Strecke \(\overline{XY}\) – sei in 3 Lagen \(E_1\), \(E_2\) und \(E_3\) in der Bezugsebene \(E_0\) gegeben. Dann gilt:
Jeder Punkt der Ebene E ist als Kreispunkt und jeder Punkt der Bezugsebene \(E_0\) ist als Mittelpunkt geeignet.
Zu einem Kreispunkt X gehört im allgemeinen ein einziger Mittelpunkt \(X_0\), der als Schnittpunkt von 2 der 3 Mittelsenkrechten \(x_{12}\), \(x_{13}\) und \(x_{23}\) zu konstruieren ist.
Ebenso gehört zu einem Mittelpunkt \(Y_0\) in \(E_0\) ein einziger Kreispunkt Y in E. Er wird in E als Schnittpunkt der Mittelsenkrechten \(y_{0.12}, y_{0.23}\) und \(y_{0.13}\) der relativen Lagen \(Y_{0.1}\), \(Y_{0.2}\) und \(Y_{0.3}\) von \(Y_0\) bezüglich E ermittelt (TP).
Die 3 Lagen der Ebene E bestimmen in der Bezugsebene \(E_0\) eindeutig 3 Pole \(P_{12}\), \(P_{13}\) und \(P_{23}\), die in \(E_0\) ein Poldreieck bilden.
Umgekehrt bestimmt ein Poldreieck 3 Lagen einer Ebene E in der Bezugsebene \(E_0\) eindeutig. Die Pole des Poldreiecks werden als Schnittpunkt der Mittelsenkrechten für die Verbindungsgeraden homologer Punkte der Ebenenlagen bestimmt.
Wenn E in \(E_0\) in 3 Lagen gegeben ist, so nimmt auch die Bezugsebene \(E_0\) – gekennzeichnet z. B. durch eine Strecke \(\overline{X_0 Y_0}\) – gegenüber der Ebene E 3 Lagen \(E_{0.1}\), \(E_{0.2}\) und \(E_{0.3}\) ein. Die Lagen lassen sich auf ein die Ebene E darstellendes TP übertragen und bestimmen analog zum Poldreieck in \(E_0\) ein durch 3 Pole bestimmtes Poldreieck in der Ebene E.
Wird Ebene E in die Lage \(E_1\) gebracht, so stimmen die Pole mit der gemeinsamen Indexziffer 1 \(P_{12}\) und \(P_{13}\) überein. Überträgt man nun den Pol \(P_{23}\) von E in \(E_0\) – \(P_{23}^1\) – so ist zu erkennen, dass dieser symmetrisch bezüglich der Poldreieckseite \(P_{12}P_{13}\) liegt – Spiegelpol.
Jeder Poldreieckswinkel ist halb so groß wie der entsprechende Drehwinkel der Ebene.
Wählt man einen Kreispunkt \(Z_2\) auf der durch die Punkte X und Y gekennzeichneten Ebene E so, dass dieser in der Lage 2 gerade mit dem Pol \(P_{23}\) in \(E_0\) übereinstimmt, so liegt gleichzeitig \(Z_3\) der Lage 3 im Pol \(P_{23}\).
Das führt dazu, dass beim Kreispunkt Z eine Punktlagenreduktion auftritt. Die im allgemeinen getrennt liegenden homologen Punkte – z. B. \(X_1\), \(X_2\) und \(X_3\) – reduzieren sich auf die Punkte \(Z_1\) und \(Z_2 ≡ Z_3\).
Dadurch sind dem Kreispunkt Z nicht nur ein Mittelpunkt Z0, sondern \(\infty^1\) Mittelpunkte auf der mit der Poldreieckseite \(P_{12}P_{13}\) identischen Mittelsenkrechten \(z_{12} = z_{13}\) zugeordnet.
Satz:
Wird ein Kreispunkt (Mittelpunkt) in einem Pol von E (\(E_0\)) gewählt, so sind ihm \(\infty^1\) Mittelpunkte (Kreispunkte) zugeordnet, die auf der gegenüberliegenden Poldreieckseite liegen.