Nachgiebige Mechanismen

Als nachgiebige Mechanismen werden Mechanismen bezeichnet, deren Funktion nicht durch konventionelle Gelenke oder Führungen ermöglicht wird (in denen Oberflächen aufeinander gleiten oder rollen) sondern durch die bewusste Ausnutzung elastischer Dehnungen an Stellen, die explizit dafür konzipiert sind. Diese sind bei nachgiebigen Mechanismen mit konzentrierter Nachgiebigkeit lokale Bereiche geringer Steifigkeit (Festkörpergelenke), bei nachgiebigen Mechanismen mit verteilter Nachgiebigkeit längere Biege- oder Torsionsfedern.

Mechanismen sind Vorrichtungen, die bewusst ausgeprägte Verformungen zulassen, um eine bestimmte Funktion zu erfüllen. Nehmen wir als einfache Beispiele zwei Handwerkzeuge: Den handelsüblichen, zangenartigen Nussknacker und die Pinzette. In beiden Beispielen wird die relative Schwenkung zweier stabförmigen Elemente (Glieder) zugelassen. Die dadurch zu erfüllende Funktion ist die Übertragung der Handkraft an eine andere Stelle. Dabei wird aufgrund des Hebelprinzips die Kraft verstärkt (beim Nussknacker) bzw. abgeschwächt (bei der Pinzette). Wichtig ist dabei zu beobachten, dass abgesehen von der gewünschten, für die Funktion des Mechanismus notwendigen Verformung, der Mechanismus steif, idealerweise starr bleiben soll. Wenn beispielsweise die Glieder keine ausreichende Steifigkeit besitzen würden, könnten sie kaum Kräfte übertragen. Wiederum soll die funktionelle Bewegung der Mechanismus so wenig Energie wie möglich erfordern. Das Schwenken der Glieder bei einer Pinzette kostet wesentlich weniger Energie als etwa das Krümmen eines der Stäbe in sich; beim Nussknacker ist dieses Verhältnis noch ausgeprägter, denn dort (abgesehen von Reibungsverlusten) die Schwenkung des (unbelasteten) Mechanismus ohne die überwindung einer Gegenkraft vonstattengeht.
Als Mechanismen sind der Nussknacker und die Pinzette nach zwei unterschiedlichen Prinzipien konzipiert. Im ersten Fall wird die Funktion des Mechanismus durch den Einbau eines Bolzengelenks zwischen zwei steifen Elementen ermöglicht. Im zweiten Fall sorgt die Elastizität bestimmter Bereiche der Konstruktion für die notwendige Schwenkung. Das macht den Unterschied zwischen konventionellen und nachgiebigen Mechanismen aus: Der Nussknacker ist ein Mechanismus der konventionellen Art, während die Pinzette ein nachgiebiger Mechanismus ist.
Viele der Vorteile nachgiebiger Systeme liegen auf der Hand: Sie sind spiel-, verschleiß- und reibungsfrei. Sie benötigen grundsätzlich keine Schmierung. Sie können in einem Stück gefertigt werden, ohne aufwendige Montageprozeduren. Durch das Fehlen von Spalten und sonstige Diskontinuitäten an der Oberfläche sind sie einfacher zu reinigen. Sie setzen aufgrund des fehlenden Verschleißes keine Partikel frei. Sie können ungehindert in stark verschmutzter Umgebung eingesetzt werdenund sind außerdem leiser. Eine weitere Reihe von Vorteilen resultiert aus spezifischen Analysen: Nachgiebiger Mechanismen sind präziser,einfacher zu miniaturisieren und leichtbaufähig.
Zu den Nachteilen nachgiebiger Mechanismen gehört eine grundsätzliche Beschränkung der Verformung aufgrund der begrenzten zuläßigen Dehnung. Außerdem ist der Entwurf nachgiebiger Mechanismen aus Gründen, die weiter unten erklärt werden, wesentlich komplexer.

 

Trotz der zahlreichen Vorteile nachgiebiger Mechanismen ist der Maschinenbau von konventionellen Mechanismen dominiert. Einer der Gründe davon ist die oben angesprochene, wesentlich höhere Komplexität des Entwurfes nachgiebiger Mechanismen im Vergleich zu konventionellen. Das Personal unseres Instituts, das sich mit nachgiebigen Mechanismen beschäftigt, hat zum Teil jahrzehntelange Erfahrung mit der Thematik deren Entwurfes und entwickelt diesen Schwerpunkt in gezielter Forschungsarbeit kontinuierlich weiter.
Der Entwurf konventioneller Mechanismen profitiert von einer wichtigen Tatsache: Deren gewünschte Verformungen resultieren aus relativen Starrkörperbewegungen der Glieder zueinander. Daher lassen sich diese grundsätzlich ohne Berücksichtigung von Kräften und elastischen Verformungen analysieren. Im Entwurf ist die Festlegung der gewünschten Verformungen eine rein topologisch-geometrische Aufgabe. Erst in einer nachgeordneten Phase werden die einzelnen Elemente (Glieder und Gelenke) dimensioniert. Der kinematische Aspekt (also die Betrachtung der gewünschten, funktionellen Verformungen) kann daher vom statischen Aspekt (die Betrachtung von Kräften und daraus resultierenden Beanspruchungen im Material) komplett getrennt werden. Das ist bei nachgiebigen Mechanismen nicht möglich. Ein stoffschlüssiges System, das ohne die Berücksichtigung von elastischen Dehnungen modelliert wird, wäre nicht in der Lage, eine gewünschte Verformung abzubilden. Das Verhältnis zwischen Kraft und Verformung muss also bei nachgiebigen Mechanismen im Entwurf vom ersten Schritt an beachtet werden. Außerdem sind Anforderungskonflikte zwischen Verformbarkeit und Belastbarkeit bei konventionellen Mechanismen wesentlich unproblematischer zu lösen, da diese Eigenschaften getrennten Komponenten zugeordnet werden: Glieder und Gelenke können beliebig versteift werden, ohne dass sich das auf die Kinematik (also auf die Realisierbarkeit der gewünschten Verformungen) negativ auswirkt. Bei nachgiebigen Systemen müssen in jedem Punkt des Systems Verformbarkeit und Belastbarkeit miteinander aufgewogen werden: Wird ein Querschnitt verstärkt, so wirkt sich das einerseits positiv auf die Belastbarkeit, andererseits negativ auf die Verformbarkeit. Aus diesem Grund wird der Entwurf nachgiebiger Systemen ab einer gewissen Komplexität grundsätzlich auf der Basis einer formell aufgestellten Optimierungsaufgabe durchgeführt.
Eine Optimierungsaufgabe besteht aus verschiedenen Teilaufgaben, für die unterschiedliches Spezialwissen gefordert ist. Erstens (Parametrisierung) muss zur mathematischen Erfassung der Gegenstand des Entwurfes (bei gegebenem, konstanten Material die unbekannte Geometrie des Mechanismus) parametrisiert werden, so dass sie als Funktion einer bestimmten Anzahl von Variablen (Entwurfsvariablen) ausgedruckt werden kann. Zweitens (Problemformulierung) muss definiert werden, welche mathematische Funktion der Entwurfsvariablen (Zielfunktion) minimiert oder maximiert werden und unter welchen Einschränkungen (Restriktionen) dies geschehen soll. Und drittens (Suchstrategie) muss das Algorithmus gewählt werden, durch das die optimale Lösung gefunden werden soll.
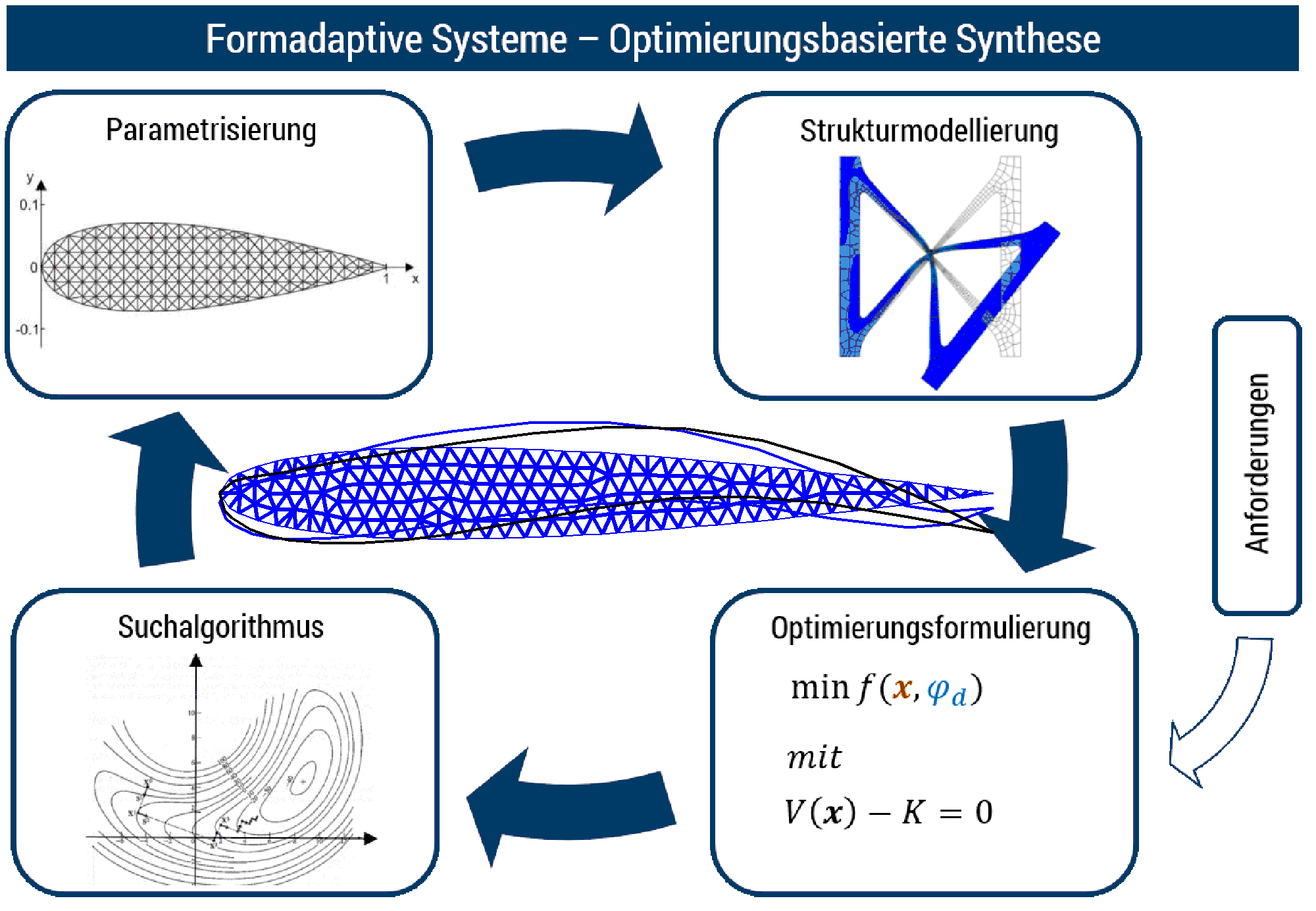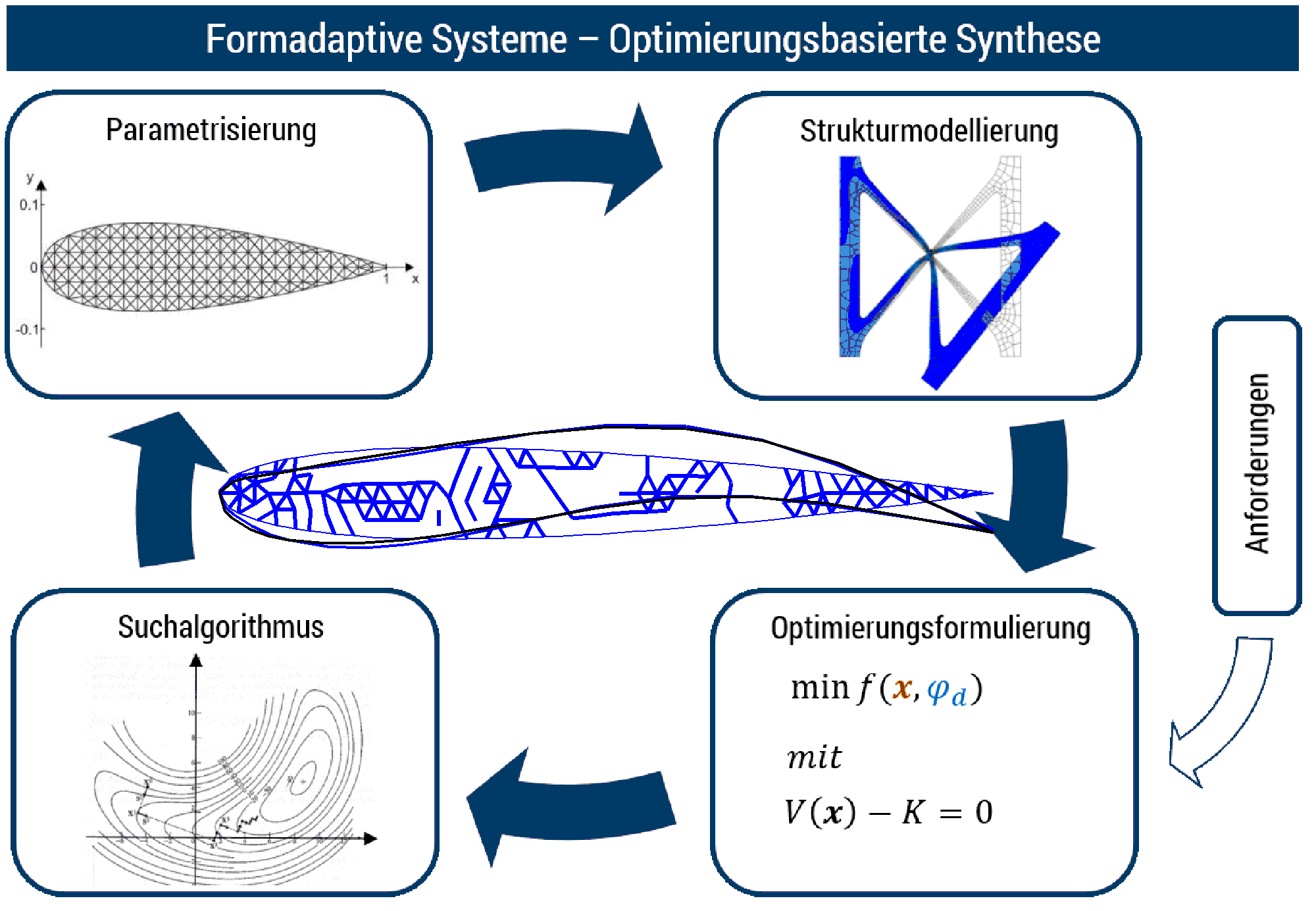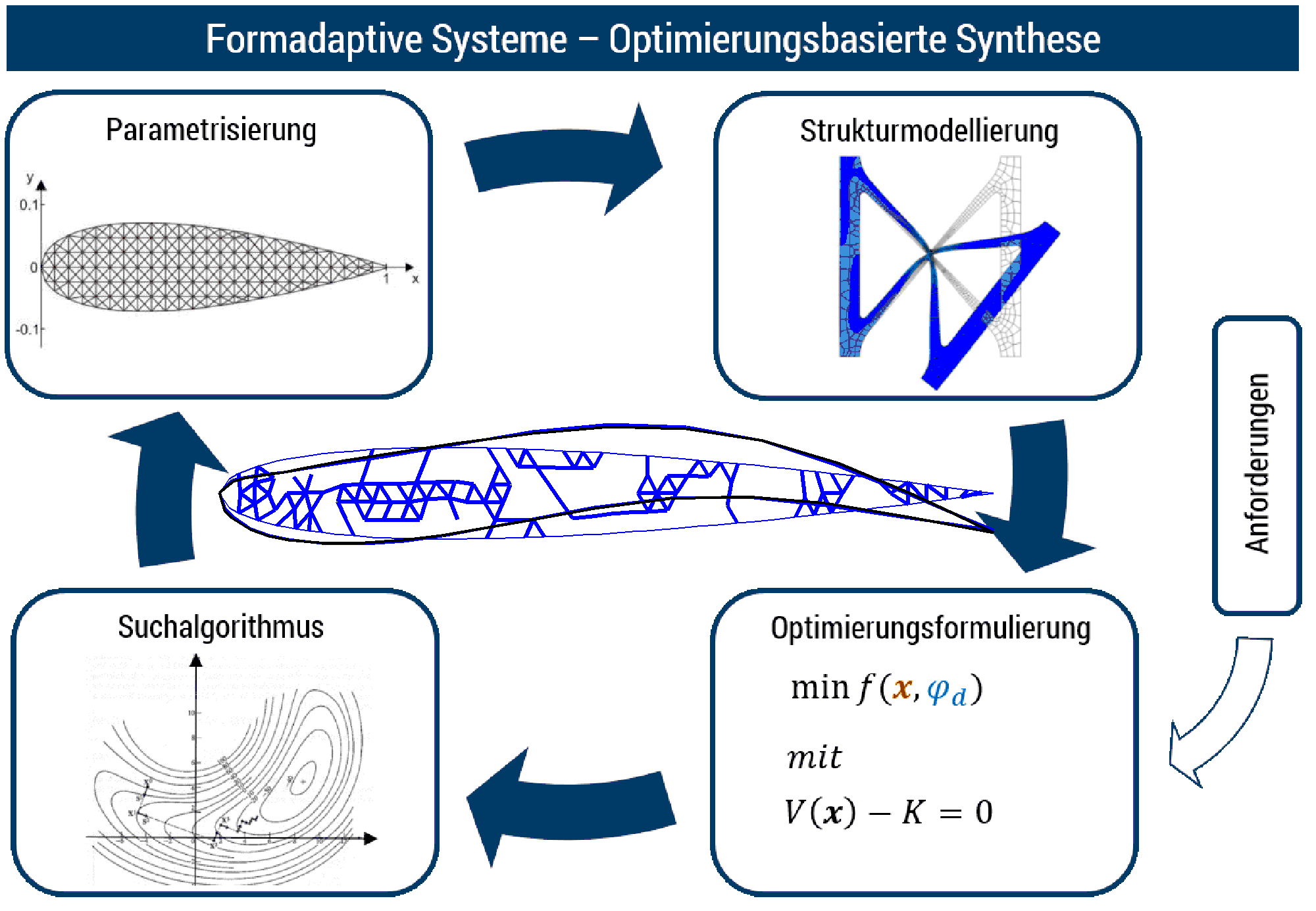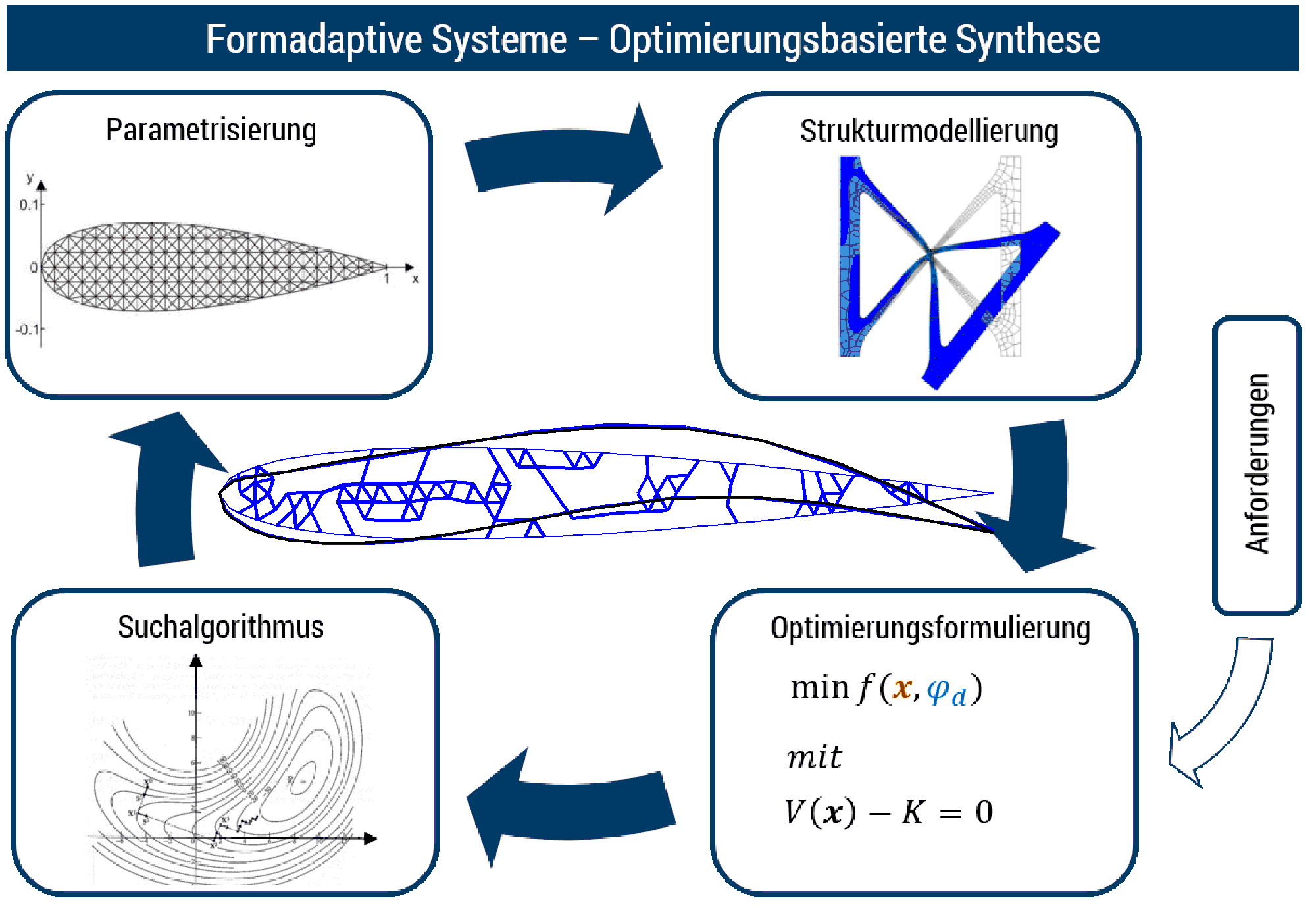Was unsere Forschung auf dem Gebiet des Entwurfes nachgiebiger Mechanismen angeht, liegt der hauptsächliche Schwerpunkt in der Untersuchung geeigneter Problemformulierungen. Was die Parametrisierung angeht, sind wir auf die sogenannte Topologieoptimierung spezialisiert, bei denen die Domäne, in der die Geometrie definiert werden soll, in einem feinen Netz von Elementen aufgeteilt wird. Der Beitrag der einzelnen Elemente zur Steifigkeit des Systems wird mit einem Faktor (Dichte) skaliert. Die Dichten der einzelnen Elemente stellen dann die Entwurfsvariablen dar. Ein spezielles Thema, das am Institut in diesem Zusammenhang behandelt wird, ist der integrierte Entwurf von nachgiebigen Mechanismen und Aktoren, die für die Aktivierung der Mechanismen sorgen.

Im Rahmen der Frage der Problemformulierung ist uns gelungen, mit der modalen Prozedur, welche das erste Beispiel sogenannter pseudokinematischer Ansätze darstellt, einen Meilenstein zu setzen.
Es wurde oben angesprochen, dass eine strenge Trennung zwischen Kinematik und Statik im Entwurf nachgiebiger Systeme nicht möglich ist. Das hat die Wissenschaftsgemeinde dazu verleitet, den Anspruch eines kinematischen Entwurfs komplett aufzugeben und Entwurfsmethoden grundsätzlich lastfallorientiert zu konzipieren. Das heißt, in der Problemformulierung wird eine begrenzte Anzahl von Lastfällen berücksichtigt und die Antwort des Systems auf abweichende Lastfälle wird nicht beachtet. Bei unserer Arbeit haben wir hingegen nach Wegen gesucht, den kinematischen Anspruch beim Entwurf so weit wie es geht aufrecht zu erhalten, und die Geometrie des Systems dafür zu optimieren, dass es dazu tendiert, für eine sehr breite Auswahl an Lastfällen mit stark ähnlichen Verformungen zu reagieren. Diese Eigenschaft (kleine Differenzen in der Verformung bei ausgeprägten Unterschieden in der Belastung) haben wir Selektivität genannt. Eine hohe Selektivität haben wir grundsätzlich zum Hauptziel der Optimierung gemacht und haben uns dann darauf fokussiert, der Selektivität eine mathematische Entsprechung zu geben, um die Maximierung der Selektivität in entsprechende Problemformulierungen umzusetzen. Diesen Ansatz nennen wir pseudokinematisch.
Bei konventionellen Mechanismen (solange sie als Systeme von Starrkörpern und perfekten Gelenken idealisiert werden) ist die Selektivität im absoluten Sinn gegeben, denn es existiert eine unendliche Anzahl von Belastungen, die zu genau der gleichen Verformung führen. Bei nachgiebigen Mechanismen ist hingegen die Selektivität eine quantitative Größe, da wie gesagt jede Verformung mit einer ganz bestimmten Belastung gekoppelt ist und so nicht möglich ist, dass zwei unterschiedlichen Belastungen zur gleichen Verformung führen. Vertiefen wir diese Tatsache mathematisch im einfachen Fall linearer Systeme, so kommen wir zur Grundlage der modalen Prozedur.
Betrachten wir zuerst einen ebenen, konventionellen Mechanismus bei kleinen Verformungen. Der Mechanismus wird mit der Methode der Finiten Elemente modelliert, wobei die Glieder nicht mehr als ideal starr gelten, sondern mit endlicher Steifigkeit versehen werden. Eins der Glieder wird fest eingespannt. Die FE-Methode liefert dann die Beziehung zwischen Verschiebungen und Kräften in Form eines Systems von linearen Gleichungen. Da wir einen Mechanismus haben, ist die Koeffizientenmatrix der Verschiebungen (die Steifigkeitsmatrix) singulär. Das bedingt, dass das System entweder gar keine Lösung hat, oder unendlich viele Lösungen. So kann es die oben angesprochene eindeutige Kopplung zwischen Belastung und Verformung nicht geben: Die meisten Belastungen führen nicht zu einer Lösung, und wiederum gibt es Lösungen, die mit unterschiedlichen Belastungen realisierbar sind. Modellieren wir wiederum einen nachgiebigen Mechanismus auf ähnliche Art und Weise, so ist die oben erwähnte Kopplung gegeben. Die Steifigkeitsmatrix ist regulär, das System immer invertierbar. Für jede gegebene Belastung gibt es eine einzige statische Lösung und umgekehrt. Allerdings wird es passieren, dass mit unterschiedlichen Belastungen sehr ähnliche Verformungen zu realisieren sind. Diese Eigenschaft (die Selektivität) findet man in der sogenannten Kondition der Steifigkeitsmatrix wieder, die wiederum mit den Eigenwerten der Steifigkeitsmatrix in Beziehung steht. Bei singulären Matrizen ist mindestens ein Eigenwert gleich Null. Die Zahl der verschwindenden Eigenwerte einer singularen Matrix wird Rangabfall R der Matrix bezeichnet und beziffert die Zahl der Reihen der Matrix, die als Linearkombination der anderen ausgedruckt werden können. Damit Lösungen existieren, müssen die gleichen Verhältnisse auch auf der rechten Seite der Gleichungen herrschen, so dass R ganze Gleichungen als Linearkombination anderer Gleichungen ausgedrückt werden können. Es ist naheliegend, dass sich eine Steifigkeitsmatrix mit einem Eigenwert, der sehr klein in Bezug auf die anderen ist (schlecht konditionierte Matrix) näherungsweise wie eine singuläre Matrix verhält. Es wird zwar strenggenommen für jede aufgeprägte Belastung unterschiedliche Lösungen geben, aber sie werden näherungsweise das gleiche Verhältnis zwischen den einzelnen Verschiebungen aufweisen. Dieses Verhältnis ist durch den Eigenvektor gegeben, der dem sehr kleinen Eigenwert zugeordnet wird.
Gelingt beim Entwurf, die Steifigkeitsmatrix so zu beeinflussen, dass ein Eigenwert gering in Bezug auf die Anderen ist und dass der entsprechende Eigenvektor die gewünschte Verformung abbildet, so wird der Entwurf des Systems methodisch in die Nähe des kinematischen Entwurfs konventioneller Systeme gebracht, da eine bestimmte Verformung lastfallunabhängig dem System als bevorzugte Verformung eingeprägt wird.
Darin besteht die modale Prozedur, die naturgemäß in dieser Form nur für lineare Systeme gilt. Sie wurde hinsichtlich der konkreten Formulierung sowie hinsichtlich algorithmischer Aspekte seit der ersten Formulierung aus 2008 schrittweise weiterentwickelt und wird gerade als Basis einer allgemeineren, pseudokinematischen Prozedur verwendet, die auch für nichtlineare Systeme gilt.
Abgesehen von der Lastfallunabhängigkeit stellt die modale Prozedur auch aufgrund ihrer Einsatzflexibilität einen Quantensprung bei der Forschung um den Entwurf nachgiebiger Mechanismen dar. Sie kann ohne aufwendige änderungen der Formulierung auf Systeme mit einer über eine große Anzahl von Freiheitsgraden definierte Kinematik angewendet werden, sowie auf sogenannte nachgiebige Mechanismen mit mehrfachen Pseudolaufgrad. Nachgiebige Mechanismen mit mehrfachen Pseudolaufgrad sind die nachgiebige Entsprechung konventioneller Mechanismen mit mehrfachem Laufgrad, also von Mechanismen, die mehr als einen Freiheitsgrad besitzen, wenn sie als Systeme von Starrkörpern und idealen Gelenken abgebildet werden.

In der unten gezeigten Tabelle können die Programmcodes über die Links heruntergeladen werden.

Papertitel	Erstautor*in	Link Professurseite	Link Mendely Data
Synthesis of compliant mechanisms with selective compliance - An advanced procedure	Kirmse	www.tu-chemnitz.de/mb/mp/mmt	https://data.mendeley.com/datasets/697dnbtz62/2
How to prestress compliant mechanisms for a targeted stiffness adjustment	Mauser	www.tu-chemnitz.de/mb/mp/sms	-
Topology-optimization based design of multi-degree-of-freedom compliant mechanisms (mechanisms with multiple pseudo-mobility)	Seltmann	www.tu-chemnitz.de/mb/mp/jimss	https://data.mendeley.com/datasets/c5k9xnyvtb/1
Topology optimization of compliant mechanisms with distributed compliance (hinge-free compliant mechanisms) by using stiffness and adaptive volume constraints instead of stress constraints	Seltmann	www.tu-chemnitz.de/mb/mp/mmt22	https://data.mendeley.com/datasets/wzzdvf8nts/2