Themenangebote für das Sommersemester 2024 und das Wintesemester 2024/25
Stand: 26. Februar 2024; 08:00 Uhr
Physikstudenten wählen bitte zehn verschiedene Versuche; Studierende des Studienganges Sensorik und kognitive Psychologie fünf Versuche aus fünf verschiedenen Professuren.

V1 - Mikrostruktur polymerer Materialien
V1 - Mikrostruktur polymerer Materialien
Versuchsbeschreibung
Polymere Materialien sind sehr haufig Mischungen verschiedener Komponenten, z.B. enthält schlagzähes Polystyrol (high-impact polystyrene, HIPS) etwas weiches Polybutadien, das die Elastizitat des Materials verbessert. Teilkristalline Polymere, wie z.B. Polyethylen und Polypropylen, bestehen aus festen kristallinen Bereichen, die in einer amorphen Matrix eingebettet sind. Diese Mikrostruktur ist die Ursache fur die hohe Schlagzähigkeit teilkristalliner Polymere. In dem Versuch soll die Gefügestruktur eines ausgewählten polymeren Materials mit optischer Mikroskopie, Rasterkraftmikroskopie und statischer Kraftspektroskopie untersucht werden. Bevorzugt sollen die Versuchsteilnehmer ein Material selbst vorschlagen oder mitbringen; alternativ stehen verschiedene technische Polymere zur Verfugung.
Professur
Chemische Physik (Prof. Dr. Robert Magerle)
Raum: C60.108
Versuchsbetreuer
Dr. Martin Dehnert
- Raum C60.110
- Tel. 0371 / 531 …
- E-Mail: martin.dehnert@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V2 - Molekulardynamik-Simulation zweidimensionaler Flüssigkeiten
V2 - Molekulardynamik-Simulation zweidimensionaler Flüssigkeiten
Versuchsbeschreibung
Molekulardynamik-Simulation bieten eine gute Möglichkeit dynamische und strukturelle Eigenschaften verschiedenster Materialien in unterschiedlichen Umgebungen auf molekularer Ebene zu untersuchen. In diesem Versuch soll insbesondere das Phasenverhalten einer zweidimensionalen Flüssigkeit im kanonischen Ensemble analysiert werden. Dabei werden eine feste Anzahl wechselwirkender Teilchen in einem festen Volumen für unterschiedliche Temperaturen simuliert und in ihrem Gleichgewichtszustand untersucht. Die zugehörigen Newtonschen Bewegungsgleichungen können z.B. mithilfe des seit 2007 als Python-Paket entwickelte Simulationstools HOOMD-blue numerisch effektiv gelöst werden. Ein Minimalbeispiel als Einstiegshilfe wird bereitgestellt. Es ist darauf zu achten, dass HOOMD-blue ein eigenständiges selbstkonsistentes Einheitensystem benutzt. Physikalische Größen werden dabei wie üblich als eine Kombination aus Zahl und Einheit dargestellt, wobei alle Einheiten eine Kombination aus den Basiseinheiten Energie, Länge und Masse sind. Details zur Umrechnung in andere Einheitensysteme können in der HOOMD-blue-Dokumentation nachgelesen werden. Die Simulationsergebnisse sollen anschließend u.a. mithilfe der Visualisierungs- und Analysesoftware Ovito ausgewertet werden, um das thermodynamische Verhalten und auftretende Phasenübergänge qualitativ und quantitativ zu charakterisieren.
Professur
Chemische Physik (Prof. Dr. Robert Magerle)
Raum: C60.110
Versuchsbetreuer
Dr. Paul Zech
- Raum C60.110
- Tel. 0371 / 531 …
- E-Mail: paul.zech@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V3 - Intensitätsmodulierte Spektroskopie an organischen Solarzellen
V3 - Intensitätsmodulierte Spektroskopie an organischen Solarzellen
Versuchsbeschreibung
Der Versuch behandelt zwei Schwerpunkte in der aktuellen Forschung an organischer Photovoltaik. Im ersten Themenbereich soll der Idealitätsfaktor n_id einer organischen Solarzelle bei Raumtemperatur möglichst genau bestimmt werden. Zu diesem Zweck werden drei verschiedene Messmethoden angewandt und deren Vor- und Nachteile gegeneinander aufgewogen. Darüber hinaus soll die Ladungsträgerbeweglichkeit µ durch Messung der Transitzeit ermittelt werden.
Professur
Optik und Photonik kondensierter Materie, insbesondere für Sensorik und Analytik (Prof. Dr. Carsten Deibel)
Raum: C60.159
Versuchsbetreuer
M. Sc. Christopher Wöpke
- Raum C60.159
- Tel. 0371 / 531 …
- E-Mail: christopher.woepke@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V5 - Raman-Spektroskopie an 2D-Materialien
V5 - Raman-Spektroskopie an 2D-Materialien
Versuchsbeschreibung
Beim Raman-Effekt stehen Licht und Materie miteinander in Wechselwirkung. Die auf die Probe eingestrahlten Photonen können in einem Feststoff (z.B. einem Halbleiterkristall) oder in einem Molekül an Schwingungen inelastisch gestreut werden. Die dafür erforderliche Energie geht dem Photon verloren (Stokes-Verschiebung) bzw. wird dem Photon hinzugefügt (Anti-Stokes-Verschiebung). Mit einem hochauflösenden Spektrometer kann die Änderung der Photonenenergie detektiert und einer bestimmten Schwingungsmode zugeordnet werden. Jede Schwingungsmode gehorcht bestimmten Raman-Auswahlregeln, die von ihren Kristallsymmetrieelementen und der Streugeometrie abhängen. Die polarisationsabhängige Raman-Spektroskopie wird eingesetzt, um die Raman-Auswahlregeln von 2D-Halbleitern zu untersuchen.
Professur
Halbleiterphysik (Prof. Dr. D. R. T. Zahn)
Raum: C60.120
Versuchsbetreuer
N.N.
- Raum C60.NN
- Tel. 0371 / 531 …
- E-Mail: nn.nn@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V6 - Nano-Infrarot-Spektroskopie
V6 - Nano-Infrarot-Spektroskopie
Versuchsbeschreibung
Nano-Infrarot-Spektroskopie gehört zu den Rastersondenmethoden, und kann als Kombination von Rasterkraftmikroskopie (AFM) mit FTIR verstanden werden. Es ist eine Erweiterung der optischen Nahfeldmikroskopie (scattering Scanning Optical Nearfield Microscopy, s-SNOM), bei der die oszillierende Spitze eines AFM von einer Lichtquelle beleuchtet wird und die Intensität des gestreuten Lichtes erfasst wird. Aus dieser Intensität kann durch Demodulation mit der Frequenz der Spitzenvibration das optische Nahfeld extrahiert werden, das nur für den Bereich direkt unter der Spitze nicht vernachlässigbar ist. Dadurch sind mit s-SNOM räumliche Auflösungen der optischen Eigenschaften im Bereich des Radius der AFM-Spitze möglich. Nano-FTIR erweitert das s-SNOM um die Fähigkeit, mit derselben Auflösung FTIR Spektren zu messen. Ein typischer Nano-FTIR-Aufbau besteht aus einem Rasterkraftmikroskop, einer Breitband-Infrarotlichtquelle und einem Michelson-Interferometer, das als Fourier-Transform-Spektrometer fungiert. Für einen guten Überblick über die Theorie von Nano-FTIR ist die Doktorarbeit von Florian Huth zu empfehlen.
Professur
Halbleiterphysik (Prof. Dr. D. R. T. Zahn)
Raum: MAIN
Versuchsbetreuer
M. Sc. Lukas Hertling
- Tel. 0371 / 531 …
- E-Mail: lukas.hertling@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V7 - Rasterelektronenmikroskopie und EBSD
V7 - Rasterelektronenmikroskopie und EBSD
Versuchsbeschreibung
Rasterelektronenmikroskope (engl. scanning electron microscope – SEM) können eine Auflösung im Bereich weniger Nanometer erreichen, was um etwa 2 Größenordnungen besser ist als bei einem Lichtmikroskop. Dazu wird ein fein fokussierter Elektronenstrahl zeilenweise über die Probe geführt. Dabei werden aus der Probenoberfläche Elektronen unterschiedlicher Energie freigesetzt. Die Intensitäten dieser Sekundär- oder Rückstreuelektronen werden für jeden Rasterpunkt des Elektronenstrahls gemessen und als Helligkeitswert zu einer Mikroskopie-Aufnahme zusammengesetzt. Daneben steht in einem SEM eine Vielzahl weiterer Signale zur Verfügung, die aus der Wechselwirkung des Elektronenstrahls mit der Probe resultieren und folglich verschiedene Informationen über die Probe enthalten. Die Auswertung dieser Signale wird unter dem Begriff der analytischen Rasterelektronenmikroskopie
Professur
Analytik an Festkörperoberflächen (Prof. Dr. Christoph Tegenkamp)
Raum: C60.U09
Versuchsbetreuer
Dr. Herbert Schletter
- Raum C10.011
- Tel. 0371 / 531 …
- E-Mail: herbert.schletter@…
Doreen Dentel
- Raum C60.010
- Tel. 0371 / 531 …
- E-Mail: doreen.dentel@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V8 - Analytische Raster-Tunnel-Mikroskopie
V8 - Analytische Raster-Tunnel-Mikroskopie
Versuchsbeschreibung
Die Rastertunnelmikroskopie (scanning tunneling microscopy - STM) ist ein Abbildungsverfahren, das - wie der Name schon sagt - auf dem quantenmechanischen Tunneleffekt beruht. Dazu wird eine metallische Spitze soweit an die Oberfläche einer (leitfähigen) Probe herangeführt, dass ein messbarer Tunnelstrom fließt. Der Abstand zwischen Spitze und Probe liegt dabei in der Größenordnung von 1 nm. Der Betrag des Tunnelstroms weist eine starke Abhängigkeit vom Abstand zwischen Spitze und Probenoberfläche auf und wird daher zur Bestimmung der Probentopografie bis in den atomaren Maßstab genutzt. Zur Erstellung eines zweidimensionalen Bildes wird die Spitze durch Piezo-Elemente über die Probe geführt und in jedem Messpunkt der Tunnelstrom bei vorgegebener Spannung gemessen.
Professur
Analytik an Festkörperoberflächen (Prof. Dr. Christoph Tegenkamp)
Raum: C60.U09
Versuchsbetreuer
Dr. Thi Ngoc Ha Nguyen
- Raum: C60.176
- Tel. 0371 / 531 …
- E-Mail: thi-ngoc-ha.nguyen@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V9 - Magnetische Anisotropie und Antiferromagnetismus in Co/Pt-Multilagen
V9 - Magnetische Anisotropie und Antiferromagnetismus in Co/Pt-Multilagen
Versuchsbeschreibung
Magnetische Multilagen, welche z.B. aus dünnen Schichten von Co und Pt bestehen, können bei geeigneten Schichtdicken eine senkrechte magnetische Anisotropie aufweisen und im entmagnetisier-ten Zustand bei entsprechender Dicke vielfältige Domänenstrukturen bilden. Des Weiteren können mittels zusätzlicher Zwischenlagen komplexere magnetische Kopplungen zwischen benachbarten Co/Pt Blöcken eingeführt werden. Bei bestimmten Schichtdicken dieser Zwischenlagen kann diese Kopplung antiferromagnetisch wirken. In diesem Fall spricht man von synthetischen geschichteten Antiferromagneten. In der angewandten Forschung werden solche Effekte häufig genutzt, um be-stimmte Funktionalitäten zu erzielen (z.B. beim magnetischen Spinventil).
Während des Versuches werden sowohl eine ferromagnetische Multilage, als auch ein darauf basie-render synthetischer Antiferromagnet, beide mit senkrechter magnetischer Anisotropie, hergestellt. Darauffolgend werden die Schichten auf ihre Eigenschaften untersucht und die Gemeinsamkeiten und Unterschiede zwischen den Schichtsysteme herausgestellt. Sie lernen dabei den Umgang mit einer konfokalen Sputterdepositionsanlage und die Bedienung üblicher Charakterisierungsgeräte zur struk-turellen (Röntgendiffraktometer) und magnetischen Analyse (Vibrating Sample Magnetometer, kurz VSM) kennen.
Professur
Magnetische Funktionsmaterialien (Prof. Dr. Olav Hellwig)
Raum: MAIN: Labor C50.038, C50.330, Physikgebäude: Labor C60.111
Versuchsbetreuer
M. Sc. Lokesh Rasabathina
- Raum C60.172
- Tel. 0371 / 531 …
- E-Mail: lokesh.rasabathina@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V10 - Photoelektronenspektroskopie (XPS)
V10 - Photoelektronenspektroskopie (XPS)
Versuchsbeschreibung
In diesem Versuch soll eine der am weitesten verbreiteten Methoden der Materialphysik kennengelernt werden: die Photoelektronenspektroskopie. Insbesondere wird die Röntgenphotoelektronenspektroskopie (XPS) behandelt.
Professur
Technische Physik (Prof. Dr. Thomas Seyller)
Raum: C60.028
Versuchsbetreuer
Dr. Fabian Göhler
- Raum C60.037
- Tel. 0371 / 531 …
- E-Mail: fabian.goehler@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V11 - Hakki-Paoli Gain-Spektroskopie
V11 - Hakki-Paoli Gain-Spektroskopie
Versuchsbeschreibung
Die Möglichkeiten der Anwendungen für Laserdioden sind vielfältig und reichen von der Beleuchtung über Projektion bis zur Datenübertragung. Die Charakterisierung von Laserdioden ist für die Forschung auch für entsprechende Anwendungen wichtig. Die Gain-Spektroskopie ist dabei eine der Möglichkeiten zur Charakterisierung.
Diese dient vor allem zur Bestimmung von internen Verlusten von Laserdioden und deren Güte.
Diese dient vor allem zur Bestimmung von internen Verlusten von Laserdioden und deren Güte.
Professur
Experimentelle Sensorik (Prof. Dr. Ulrich Theodor Schwarz)
Raum: C60.024
Versuchsbetreuer
Shemshat Kerimova
- Raum C60.039
- Tel. 0371 / 531 …
- E-Mail: shemshat.kerimova@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V12 - Neuronale Netzwerke
V12 - Neuronale Netzwerke
Versuchsbeschreibung
Seit den späten 50er Jahren des 20. Jahrhunderts werden Modelle neuronaler Netzwerke als Verfahren zum automatisierten Lernen von Strukturen und Mustern eingesetzt. Nach einer Trainingsphase mit bekannten Daten erkennen diese Modelle in zuvor unbekannten Daten die erlernten Muster wieder (z.B.: Rosenblatt, 1958; Fukushima, 1980). Die Struktur solcher Netzwerke ist von den Verarbeitungsprozessen des menschlichen Gehirns inspiriert. Dabei knüpfen jedoch sowohl die Ausgestaltung der einzelnen Recheneinheiten, die grob den menschlichen Nervenzellen entsprechen, als auch die eingesetzten Lernverfahren nur lose an das biologische Vorbild an. Während um den Jahrtausendwechsel andere Verfahren des maschinellen Lernens in den Vordergrund traten, erleben seit einigen Jahren neuronale Netzwerke, nun vor allem in Form sogenannter «tiefer Netzwerke» (engl. deep neural networks – DNNs), einen enormen Bedeutungszuwachs mit einem breiten Anwendungsfeld (für eine Übersicht siehe z.B. LeCun et al., 2015). Der Praktikumsversuch führt zunächst in die Grundlagen neuronaler Netzwerke ein. Im zweiten Teil erfolgt eine Einführung in die Verarbeitung natürlicher Reize und das Konzept der Spärlichkeit im Zusammenhang früher visueller Verarbeitung. Im dritten Teil beschäftigen wir uns mit der Klassifikation natürlicher Szenen durch ein modernes DNN-Modell, insbesondere mit dessen Fehlern und deren Ursachen.
Professur
Physik kognitiver Prozesse (Prof. Dr. Wolfgang Einhäuser-Treyer) & Struktur und Funktion kognitiver Systeme (Prof. Dr. Alexandra Bendixen)
Raum: C60.143
Versuchsbetreuer
Prof. Dr. Wolfgang Einhäuser-Treyer
- Raum C60.135
- Tel. 0371 / 531 …
- E-Mail: wolfgang.einhaeuser-treyer@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V14 - Vom Chaos zum Quantenchaos
V14 - Vom Chaos zum Quantenchaos
Versuchsbeschreibung
Der Korrespondenz zwischen klassischer Mechanik auf der einen und Quantenmechanik auf der anderen Seite - die Strahlen-Wellen-Korrespondenz - ist ein zentrales Prinzip der modernen Physik. Besonders interessant ist diese Relation in klassischen Systemen mit nichtlinearer Dynamik, sogenannten chaotischen Systemen: Wie äußern sich die Nichtlinearitäten im quanten- bzw. wellenmechanischem Pendant, welche Auswirkung hat das auf die Erhaltungsgrößen, welche Rolle spielt das nur quantenmechanisch erlaubte Tunneln? Diese Fragen sind Gegenstand des Forschungsfeldes des Quantenchaos. Dieser Versuch soll einen Einblick in die vielfältigen und komplexen Fragestellungen geben und einen ersten Zugang zu den teilweise verblüffenden Antworten ermöglichen. Zur Illustrierung wählen wir ein prominentes Modellsystem, nämlich die Klasse der Billards. Wir starten mit klassischen Billards mit harten Wänden, in denen Abweichungen von der Kreisform die nichtlineare Dynamik induzieren. Die quantenmechanische Beschreibung erfolgt mit der Schrödingergleichung. Ein Aspekt des Versuchs wird die Betrachtung von Billards für Licht sein, insbesondere unter dem Aspekt der Strahlen-Wellen-Korrespondenz.
Professur
Theoretische Physik komplexer dynamischer Systeme (Prof. Dr. Martina Hentschel)
Raum: C60.209
Versuchsbetreuer
M. Sc. Lukas Seemann
- Raum C60.213
- Tel. 0371 / 531 …
- E-Mail: lukas.seemann@…
- Raum C60.213
- Tel. 0371 / 531 …
- E-Mail: tom.rodemund@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V15 - Computergestützte Modellierung physikalischer Prozesse
V15 - Computergestützte Modellierung physikalischer Prozesse
Versuchsbeschreibung
Nicht alle physikalischen Experimente lassen sich in der echten Natur ausführen. Oft ist es zu aufwendig und zu teuer, wenn nicht sogar unmöglich, die dazu notwendigen Apparaturen und Beobachtungsgeräte zu bauen. In solchen Fällen hilft die Nachahmung der Natur (Simulation) auf dem Computer, die Probleme zu lösen.
In diesem Versuch soll ein Experiment modelliert werden, bei dem auf eine Festkörperplatte auftreffende Teilchen (z.B. Neutronen) reflektiert, absorbiert oder transmittiert/gestreut werden. Im Computerexperiment werden die Bahnen jedes einzelnen Teilchens verfolgt. Dabei treten zufällig Absorptionen oder Richtungsänderungen auf, wodurch im statistischen Mittel ein bestimmter Anteil von Teilchen reflektiert, absorbiert oder transmittiert/gestreut wird.
In diesem Versuch soll ein Experiment modelliert werden, bei dem auf eine Festkörperplatte auftreffende Teilchen (z.B. Neutronen) reflektiert, absorbiert oder transmittiert/gestreut werden. Im Computerexperiment werden die Bahnen jedes einzelnen Teilchens verfolgt. Dabei treten zufällig Absorptionen oder Richtungsänderungen auf, wodurch im statistischen Mittel ein bestimmter Anteil von Teilchen reflektiert, absorbiert oder transmittiert/gestreut wird.
Professur
Simulation naturwissenschaftlicher Prozesse (Prof. Dr. Martin Weigel)
Raum: C60.205
Versuchsbetreuer
Dr. Janett Prehl
- Raum C60.212
- Tel. 0371 / 531 …
- E-Mail: janett.prehl@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V16 - Phasen Übergang und Hysterese im Ising-Modell
V16 - Phasen Übergang und Hysterese im Ising-Modell
Versuchsbeschreibung
Das Praktikum soll den Rahmen des in der Statistischen Physik behandelten Stoffes erweitern. Neben der Betrachtung, wie ein System in einen thermodynamischen Gleichgewichtszustand relaxiert, soll ein Verständnis für Phasenübergänge und das Auftreten von Hysterese erlangt werden. Dies geschieht am Beispiel des zweidimensionalen Ising-Modells.
Um zum Verständnis des Ferromagnetismus beizutragen, wurde von Ernst Ising 1925 in der Arbeitsgruppe von Wilhelm Lenz ein System wechselwirkender Spins untersucht, das später als Ising-Modell bekannt wurde. In seiner Dissertation untersuchte Ising den eindimensionalen Fall; da dieser keinen Phasenübergang in eine geordnete ferromagnetische Phase zeigt, schloss Ising, dass das Modell nicht von größerem Interesse sei. Enttäuscht verließ er das Forschungsumfeld, wurde Lehrer und wanderte nach Verfolgung durch die Nazis nach Amerika aus. Erst 25 Jahre nach seiner Promotion erfuhr er, dass das Ising-Modell trotz seiner konzeptionellen Einfachheit zu einem Schlüsselmodell der statistischen Physik geworden war. Heute reichen die Anwendungen bis in entfernte Gebiete wie etwa die Biologie, Hirnforschung, Soziologie und Ökonomie. Inzwischen sind zehntausende von wissenschaftlichen Arbeiten veröffentlicht worden, die sich mit dem Ising-Modell befassen.
Um zum Verständnis des Ferromagnetismus beizutragen, wurde von Ernst Ising 1925 in der Arbeitsgruppe von Wilhelm Lenz ein System wechselwirkender Spins untersucht, das später als Ising-Modell bekannt wurde. In seiner Dissertation untersuchte Ising den eindimensionalen Fall; da dieser keinen Phasenübergang in eine geordnete ferromagnetische Phase zeigt, schloss Ising, dass das Modell nicht von größerem Interesse sei. Enttäuscht verließ er das Forschungsumfeld, wurde Lehrer und wanderte nach Verfolgung durch die Nazis nach Amerika aus. Erst 25 Jahre nach seiner Promotion erfuhr er, dass das Ising-Modell trotz seiner konzeptionellen Einfachheit zu einem Schlüsselmodell der statistischen Physik geworden war. Heute reichen die Anwendungen bis in entfernte Gebiete wie etwa die Biologie, Hirnforschung, Soziologie und Ökonomie. Inzwischen sind zehntausende von wissenschaftlichen Arbeiten veröffentlicht worden, die sich mit dem Ising-Modell befassen.
Professur
Simulation naturwissenschaftlicher Prozesse (Prof. Dr. Martin Weigel)
Raum: C60.209
Versuchsbetreuer
Prof. Dr. Martin Weigel
- Raum C60.211
- Tel. 0371 / 531 …
- E-Mail: martin.weigel@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V17 - Datenbasierte Modelle für komplexe physikalische Zusammenhänge (Grundlagen maschinellen Lernens)
V17 - Datenbasierte Modelle für komplexe physikalische Zusammenhänge (Grundlagen maschinellen Lernens)
Versuchsbeschreibung
Die Beschreibung physikalischer Zusammenhänge, entweder über Experimente oder numerischen Simulationen, ist oft mit hohem Kosten und Zeitaufwand verbunden. Eine vielversprechende Alternative stellen datenbasierte Ersatzmodelle dar. Hierbei handelt es sich um vergleichsweise recheneffiziente Modelle, welche wesentliche Charakteristika eines (physikalischen) Zusammenhanges abbilden können und im Vorfeld auf Basis eines anderweitig bestimmten Datensatzes trainiert werden. Ersatzmodelle kommen zunehmend in den Materialwissenschaften und der Industrie zum Einsatz und stellen daher ein vielseitiges Werkzeug sowohl für Experimentatoren und auch für Theoretiker dar.
Im vorliegenden Versuch sollen die grundlegenden Fähigkeiten zur Arbeit mit datenbasierten Ersatzmodellen vermittelt werden. Dafür werden Datensätze zur Verfügung gestellt, die anschließend unter Verwendung verschiedener Ansätze als Ersatzmodell abgebildet werden. Es kommen Ansätze aus freien Bibliotheken zum Einsatz. Diese Bibliotheken werden über die Programmiersprache Python angesprochen, jedoch sind rudimentäre Programmierkenntnisse für den Versuch ausreichend.
Im vorliegenden Versuch sollen die grundlegenden Fähigkeiten zur Arbeit mit datenbasierten Ersatzmodellen vermittelt werden. Dafür werden Datensätze zur Verfügung gestellt, die anschließend unter Verwendung verschiedener Ansätze als Ersatzmodell abgebildet werden. Es kommen Ansätze aus freien Bibliotheken zum Einsatz. Diese Bibliotheken werden über die Programmiersprache Python angesprochen, jedoch sind rudimentäre Programmierkenntnisse für den Versuch ausreichend.
Professur
Simulation von Prozessen, Anlagen und Bauelementen für die Mikro- und Nanoelektronik (Dr. Jörg Schuster, Prof. Dr. Sibylle Gemming)
Raum: C50.239
Versuchsbetreuer
Dr. Florian Fuchs
- Raum C50.101
- Tel. 0371 / 531 …
- E-Mail: florian.fuchs@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V18 - Diffusionsbegrenztes Wachstum von Clustern
V18 - Diffusionsbegrenztes Wachstum von Clustern
Versuchsbeschreibung
Der Entstehung von Schneeflocken, Bakterienkolonien, Blitzen und elektrochemischen Abscheidungen liegen offensichtlich ganz unterschiedliche physikalische Prozesse zu Grunde. Erstaunlicherweise sehen sich die resultierenden stark verzweigten Strukturen aber durchaus sehr ähnlich. Diese Beobachtung führte zu der Überlegung, dass die Strukturbildung unabhängig von den Details der wirkenden Kräfte durch nur wenige grundlegende Prinzipien erklärt werden kann.
Ein populäres Modell in diesem Gebiet ist das 1981 von Witten und Sander vorgeschlagene diffusionsbegrenzte Wachstum (diffusion limited aggregation - DLA). In Anlehnung an die Brownsche Bewegung diffundieren Teilchen auf Zufallspfaden bis sie auf eine Keimzelle oder ein bereits gebildetes Aggregat treffen und dort haften bleiben. Durch diese zufällige Anlagerung entsteht ein Cluster mit erstaunlich komplexer fraktaler Struktur. Die Eigenschaften des Clusters lassen sich zum Beispiel durch die fraktale Dimension quantifizieren.
Ein populäres Modell in diesem Gebiet ist das 1981 von Witten und Sander vorgeschlagene diffusionsbegrenzte Wachstum (diffusion limited aggregation - DLA). In Anlehnung an die Brownsche Bewegung diffundieren Teilchen auf Zufallspfaden bis sie auf eine Keimzelle oder ein bereits gebildetes Aggregat treffen und dort haften bleiben. Durch diese zufällige Anlagerung entsteht ein Cluster mit erstaunlich komplexer fraktaler Struktur. Die Eigenschaften des Clusters lassen sich zum Beispiel durch die fraktale Dimension quantifizieren.
Professur
Theoretische Physik quantenmechanischer Prozesse und Systeme (Prof. Dr. Sibylle Gemming)
Raum: C60.310, C60.313
Versuchsbetreuer
Dr. Philipp Cain
- Raum C60.310
- Tel. 0371 / 531 …
- E-Mail: cain@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)

V20 - Bewegung der Planeten im Sonnensystem
V20 - Bewegung der Planeten im Sonnensystem
Versuchsbeschreibung
Betrachten Sie die Bewegung der vier inneren Planeten unseres Sonnensystems. Setzen Sie voraus, dass sich alle Planeten in einer Ebene bewegen.
Professur
Simulation neuer Materialien (Prof. Dr. Angela Thränhardt)
Raum: C60.306
Versuchsbetreuer
M. Sc. Maik Schwuchow
- Raum C60.306
- Tel. 0371 / 531 …
- E-Mail: maik.schwuchow@…
- Raum C60.303
- Tel. 0371 / 531 …
- E-Mail: tom.witke@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)
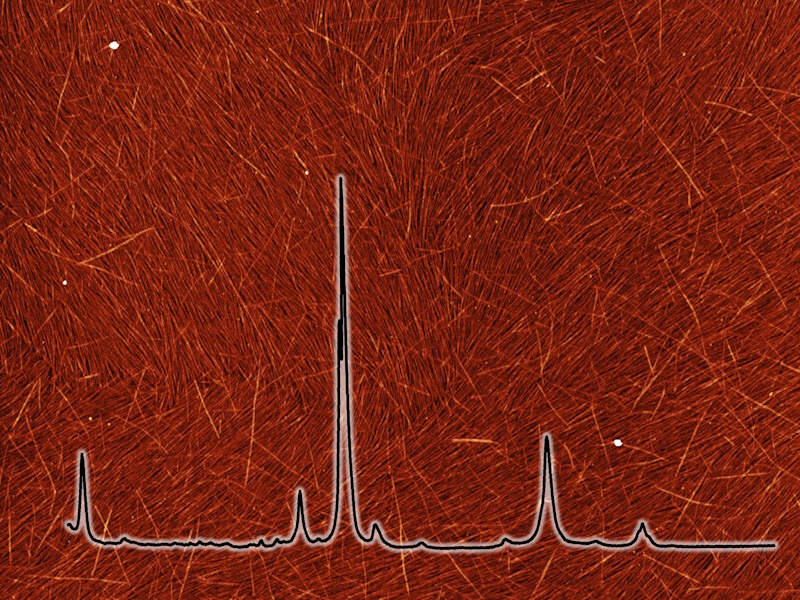
V21 - Topologische Analyse von 1D-Materialien
V21 - Topologische Analyse von 1D-Materialien
Versuchsbeschreibung
Kohlenstoffnanoröhren (CNTs) zeigen eine Reihe von hervorragenden Eigenschaften, welche diese Materialklasse sehr vielversprechend für zukünftige Mikro- und Nanoelektronik macht.
Aufgrund ihrer außergewöhnlich hohen effektiven Ladungsträgermobilität sowie thermischen und mechanischen Stabilität eignen sich CNTs hervorragend als Halbleitermaterial in elektronischen Bauelementen und integrierten Schaltkreisen.
Dabei ist eine der größten Herausforderungen das kontrollierte Aufbringen von CNTs auf eine Festkörperoberfläche (z.B. ein 200 mm Silizium Wafer).
Dabei müssen diese mit einer vorgegeben Dichte und Orientierung aufgebracht werden, um elektronische Bauelemente wie Transistoren mit einer hohen Performance zu realisieren.
Professur
Honorarprofessur Technologien der Nanoelektronik, Forschungsgruppe 1D/2D Nano Devices (Dr. Sascha Hermann)
Raum: C50.237
Versuchsbetreuer
Dr. Martin Hartmann
- Raum C50.203
- Tel. 0371 / 531 …
- E-Mail: martin.hartmann@…
Versuchsanleitung
Versuchsanleitung als PDF
(nicht barrierefrei)
