Definitions of Hidden Markov Model (HMM)

A Hidden Markov Model (HMM) is a discrete-time finite-state Markov chain coupled with a sequence of letters emitted when the Markov chain visits its states. Transitions among the states are governed by a set of probabilities called transition probabilities. In a particular state an outcome or observation can be generated, according to the associated probability distribution. It is only the outcome, not the state is visible to an external observer and therefore states are ''hidden'' to the outside. Hence the name Hidden Markov Model.

• HMM is the mainstay of statistical modeling used to model any time varying random phenomena.

• HMM is a probabilistic pattern matching technique, in which the observations are considered to be the outputs of a stochastic process and consists of an underlying Markov chain.

• HMM is a technique for modeling the temporal structure of a time series signal, or of a symbolic sequence. It is a probabilistic pattern matching approach which models a sequence of patterns as the output of a random process. The HMM consists of an underlying Markov chain.

• Markov chain: is a structure comprises stationary entities called states. The transition between/within states is probabilistic.

Mathematically a hidden Markov model (HMM) is a triple 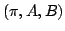$(\pi,A,B)$ such

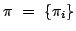$\pi  =  \{ \pi_i \}$ the vector of the initial state probabilities: $\pi_i = P(X_1=i) 1 \leq i \leq N$ ;

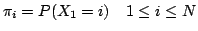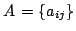$A = \{ a_{ij} \}$ the state transition matrix: $P(X_t=j\vert X_{t-1}=i) 1 \leq i,j \leq N$;

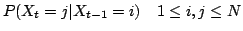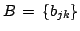$B = \{b_{jk} \}$ the emission matrix (The output distribution): $P(Y_t=k\vert X_t=j) 1 \leq i \leq N 1 \leq k \leq M$;

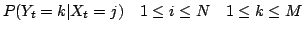Each probability in the state transition matrix and in the confusion matrix is time independent-that is, the matrices do not change in time as the system evolves. In practice, this is one of the most unrealistic assumptions of Markov models about real processes.
An example of Hidden Markov Model as shown in the figure bellow has five states, each state has three probabilities associated to it (initial, transition and output probability) and has also three observation symbols.