Adaptive anisotrope Netzsteuerung
Eine adaptive anisotrope Netzsteuerung erfordert im Laufe der Rechnung
ein automatisches Erkennen der Anisotropierichtungen sowie das Anpassen
der Elemente entlang dieser Richtungen. Dabei ist es formal und praktisch
günstig, die adaptiven Schritte aufzuteilen in die Teilaufgaben Informationsgewinnung
und Netzgenerierung/-verfeinerung.
 Informationsgewinnung
Informationsgewinnung
Bei der Informationsgewinnung sucht man diejenigen Informationen,
die ein anisotropes Element beschreiben, nämlich Streckungsrichtungen,
Streckungsverhältnisse und Elementgröße. Günstigerweise
sollten diese Informationen von einem geeigneten anisotropen Fehlerschätzer
bereitgestellt werden. Leider gelingt dies im Allgemeinen nur für
die letzte Information, die Elementgröße (Volumen).
Elementgröße:
aus lokaler Fehlergröße Ü anisotroper
Fehlerschätzer
Die ersten beiden Informationen Streckungsrichtungen und Streckungsverhältnisse
können (bisher) nicht aus Fehlerschätzern extrahiert werden.
Von verschiedenen Forschern wurden deshalb Ansätze vorgeschlagen,
die sich grob in die folgenden drei Gruppen einteilen lassen: Untersuchungen
der zweiten Ableitungen der FEM-Lösung; Betrachtung der Höhenlinien
und/oder Stromlinien; sonstige (Gradient des geschätzten Fehlers,
Verteilung gewisser Variablen etc.).
Streckungsrichtung/-verhältnis:
-
aus approximiertem Hessian



Der am häufigsten genutzte Ansatz verwendet die Matrix der zweiten
Ableitungen, d.h. die Hesse-Matrix der FEM-Lösung. Exemplarisch genannt
seien hier die Arbeiten
-
J. Peraire, M. Vahdati, K. Morgan und O.C. Zienkiewicz. Adaptive remeshing
for compressible flow computations. J. Comp. Phys., 72:449-466,
1987.
-
R. B. Simpson. Anisotropic mesh transformation and optimal error control.
Applied
Numerical Mathematics, 14:183-198, 1994.
-
V. Dolejsí. Anisotropic mesh adaptation for finite volume and finite
element methods on triangular meshes. Comput. Vis. Sci., 1(3):165-178,
1998.
-
E. D' Azevedo. On optimal bilinear quadrilateral meshes. Eng. Comput.,
15(3):219-227, 1999.
-
G. S. Buscaglia und E. A. Dari. Anisotropic mesh optimization and its application
in adaptivity. Int. J. Numer. Methods Eng., 40(22):4119-4136, 1997.
-
M. J. Castro-Díaz, F. Hecht und B. Mohammadi. New progress in anisotropic
grid adaptation for inviscid and viscous flow simulation. In Proceedings
of the 4th Annual International Meshing Roundtable,
Seiten 73-85, Albuquerque, NM, 1995. Sandia National Laboratories. Auch
Report 2671, INRIA.
-
D. Ati-Ali-Yahia, Y. Bourgault, J. Dompierre, M. Fortin, W.G. Habashi und
M-G. Vallet. Anisotropic mesh adaptation: Towards user-independent CFD
solutions: Part I: General principles. Int. J. Numer. Methods Fluids,
32:725-744, 2000.
-
aus Gradient des geschätzten Fehlers


Sonstige Ansätze betrachten überwiegend die Änderung
"geeigneter" Größen, z.B. des Gradienten der Näherungslösung,
der Dichte oder der Mach-Zahl, siehe
-
R. Beinert und D. Kröner. Finite volume methods with local mesh alignment
in 2-D. In Adaptive Methods - Algorithms, Theory and Applications, Notes
on Numerical Fluid Mechanics, Bd. 46, Seiten 38-53, Braunschweig, 1994.
Vieweg.
-
O. C. Zienkiewicz und J. Wu. Automatic directional refinement in adaptive
analysis of compressible flows. Int. J. Num. Meth. Eng., 37:2189-2210,
1994.
Darüberhinaus wird versucht, Anisotropie-Richtungen abzuleiten. Meist
sind diese Methoden weniger mathematisch fundiert, sondern eher heuristisch/praktisch
motiviert, so z.B. bei CFD-Berechnungen.
-
aus Höhenlinien, Stromlinien
Ein weiterer, anschaulich einleuchtender Ansatz nutzt die Höhenlinien
der FEM-Lösung oder Stromlinien. Diese Herangehensweise geht auf Kornhuber/Roitzsch
(1990) zurück, s.a. Scalický/Roos (1999):
-
R. Kornhuber und R. Roitzsch. On adaptive grid refinement in the presence
of internal and boundary layers. IMPACT of Computing in Sci. And Engrg.,
2:40-72, 1990.
-
T. Skalický und H. G. Roos. Anisotropic mesh refinement for problems
with internal and boundary layers. Int. J. Numer. Meth. Engrg., 46:1933-1953,
1999.
 Netzgenerierung/-verfeinerung
Netzgenerierung/-verfeinerung
Nachdem die gewünschten anisotropen Netzinformationen
bestimmt wurden, erfolgt die anisotrope Netzgenerierung/-verfeinerung.
Den
meisten anisotropen Methoden liegt eine anisotrope Transformation zugrunde.
Dabei wird lokal das Rechengebiet mit Hilfe eines anisotropen Metrik-Tensors
in ein Referenzgebiet abgebildet. Dieses wird nun isotrop
vernetzt
und zurück abgebildet, so dass im Originalgebiet ein
anisotropes
Netz entsteht.
Für die isotrope Vernetzung des Referenzgebietes
kann man auf bekannte Algorithmen zurückgreifen. In Verbindung mit
der anisotropen Metrik lassen sich ganz grob drei Strategien unterscheiden,
die zum Teil auch gemeinsam genutzt werden: Advancing-Front-Methoden;
Delaunay-Vernetzungen; Netzverbesserungs/Netzverfeinerungs-Algorithmen.
unstrukturiert:
fehlende Hierarchie für Löser


hierarchisch:
schlechte Anpassung an Krümmungen
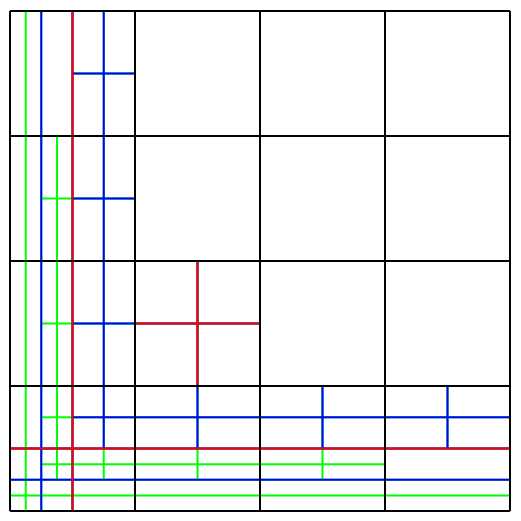
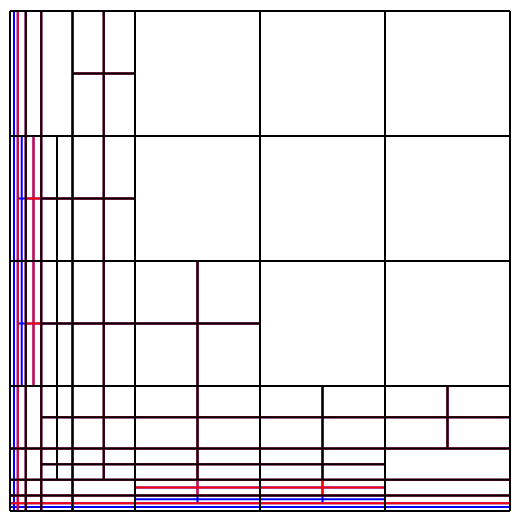
Chemnitzer Vision: Hierarchisch,
aber
Im vorangegangenen Abschnitt haben wir uns hauptsächlich auf
die Generierung und Verfeinerung der Netze konzentriert. Um jedoch auf
Netze mit sehr vielen Elementen (z.B. in 3D ab 1 Million) rechnen zu können,
benötigt man effektive Auflösungsverfahren für die entstehenden
Gleichungssysteme. Hier sind Multigrid/Multilevel-Ansätze unabdingbar
und dafür sind Netz-Hierarchien erforderlich. Die Verbindung
von Hierarchien und adaptiven anisotropen Netzen wiederum wurde in der
Literatur bisher kaum untersucht.



-
neue Knoten nicht in Kantenmitte

-
adaptive Generierung des Hauptnetzes
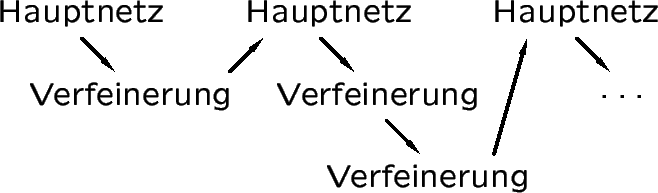


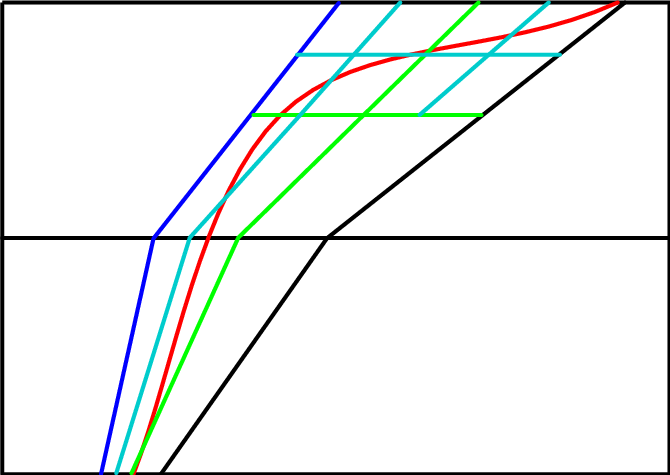
![]() Informationsgewinnung
Informationsgewinnung




![]() Netzgenerierung/-verfeinerung
Netzgenerierung/-verfeinerung











