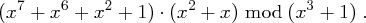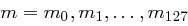, der als Bytefolge| DES | RSA |
Das National Institute of Standards and Technology der USA hat 1997 einen Wettbewerb ausgeschrieben, um einen Nachfolger für den damaligen Verschlüsselungsstandard DES zu finden. Dieser Wettbewerb endete am 2.10.2000 damit, dass das Verfahren Rijndael zum Sieger und damit zum neuen Verschlüsselungsstandard erklärt wurde.
Eingabe für das Verfahren ist ein 128 Bit langer Klartext 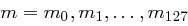, der als Bytefolge
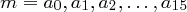
mit
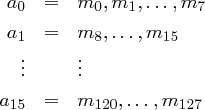
dargestellt werden kann. Diese Bytefolge wird State genannt und ist durch folgende Matrix repräsentiert, die als Grundlage für die Operationen verwendet wird.
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
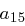Im Gegensatz zur obigen Beschreibung werden die Bits 
eines einzelnen Bytes 
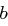im Folgenden aufsteigend von rechts nach links indiziert:
Die Verschlüsselung erfolgt in mehreren Runden, wobei die Anzahl der Runden von der Blocklänge 
und von der Schlüssellänge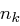 
abhängig ist, wobei gilt:
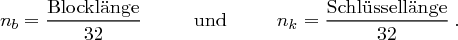
Die Anzahl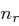 
der Runden berechnet sich dann durch
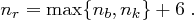
Jede außer der letzten Runde besteht aus den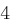 
einzelnen Operationen
Die letzte Runde verzichtet auf die MixColumns-Operation. Sämtliche durchgeführten Transformationen sind umkehrbar, so dass die Entschlüsselung lediglich die entsprechende Umkehroperationen aufrufen muss (in umgekehrter Reihenfolge). Dabei kommen die inversen Operationen InvSubBytes, InvShiftRows, InvMixColumns und AddRoundKey (diese Transformation ist selbstinvers) zum Einsatz, in der ersten Runde fehlt entsprechend der Aufruf von InvMixColumns.
Die SubBytes-Transformation, eine nichtlineare Bytesubstitution, wird auf jedes einzelne Byte eines State angewendet, wobei das Ergebnis dieser Transformation unabhängig von den anderen Bytes ist. Es sei
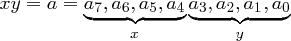
die Hexadezimaldarstellung des Bytes 
. Dann wird das Byte 
transformiert zu dem Hexadezimalwert, der in der folgenden Tabelle in Zeile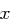 
und Spalte 
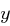enthalten ist.
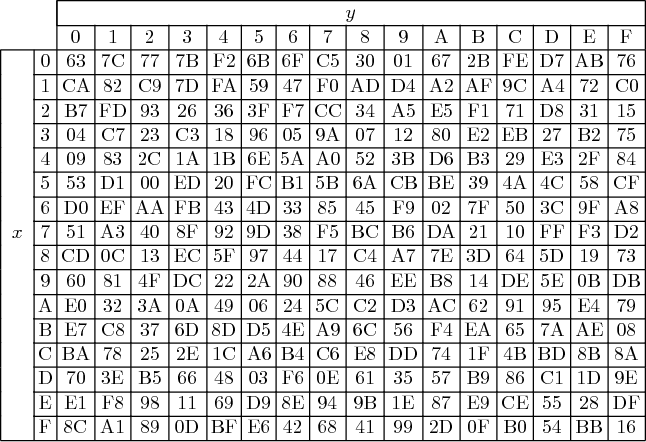
Für diese SubBytes-Transformation gibt es auch eine explizite Berechnungsvorschrift, die aus zwei einzelnen Transformationen besteht:
1. Transformation.
Gegeben sei ein Byte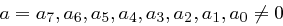 
, welches als Polynom die Darstellung 
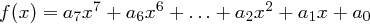hat. Die einzelnen Bits dienen jetzt als Koeffizienten. Ein wichtiger Aspekt dieser Interpretation besteht darin, dass 
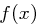ein Polynom über 
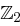darstellt; 
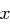kann also nur die Werte Null oder Eins annehmen. Weiterhin sind an dieser Stelle nur Polynome mit einem Grad von höchstens sieben zulässig - bei der Multiplikation kann jedoch ein Polynom höheren Grades auftreten, welches nicht mehr durch ein Byte darstellbar ist. Dieses Problem kann man dadurch lösen, dass man in Restklassenringen modulo eines Reduktionspolynoms rechnet - im hier diskutierten Zusammenhang ist dies
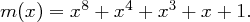
Wie funktioniert nun das Rechnen unter diesen Voraussetzungen? Polynome mit einem Grad kleiner als acht bedürfen keiner Anpassung, ihre Koeffizienten sind offenbar durch ein Byte kodierbar. Anders liegen die Dinge, wenn wir beispielsweise die Polynome
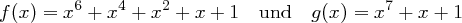
multiplizieren, wir erhalten
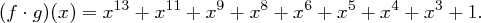
Um den Rest modulo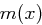 
zu bestimmen, führen wir eine schriftliche Division durch, interessieren uns dabei aber nicht für den Quotienten, sondern den entstehenden Rest. Die erste Division (
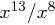) liefert 
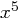, wir subtrahieren also 
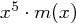von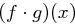 
und erhalten
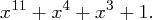
Der nächste Divisionsschritt (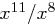
) ergibt 
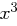, wir subtrahieren jetzt 
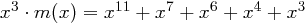. Das Resultat, 
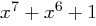, kann wieder durch ein Byte dargestellt werden. Wir sind an dieser Stelle fertig und erhalten als Rest 
.
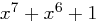Auf eine Besonderheit muss jedoch hingewiesen werden: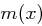 
ist irreduzibel, das heißt, es ist nur in triviale Faktoren zerlegbar. Da wir eben die mod-Operation für Polynome beschrieben haben, ist nun auch die Anwendung des erweiterten Euklidischen Algorithmus und infolgedessen die Bestimmung des Inversen möglich - es ist lediglich zu beachten, dass das Polynom 
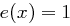das neutrale Element bezüglich der Multiplikation darstellt (in Bytedarstellung: 
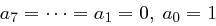) und dass 
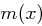(wie gesagt) irreduzibel, also nur in triviale Faktoren 
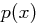und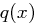 
zerlegbar ist (um Nullteilerfreiheit zu gewährleisten). Jedes Polynom 
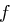mit Höchstgrad sieben hat demnach nur 
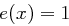als gemeinsamen Teiler mit 
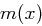. Damit sind wir in der Lage, den erweiterten Euklidischen Algorithmus anzuwenden, der Polynome 
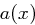und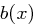 
mit der Eigenschaft
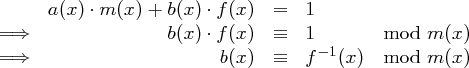
bestimmt. Um zur SubBytes-Transformation zurückzukommen: Wir wollen ein Byte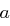 
, das mit dem Polynom 
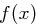korrespondiert, verarbeiten und bestimmen das inverse Polynom 
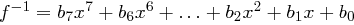. Als Ergebnis der 1. Transformation erhalten wir das Byte
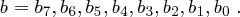
Lediglich der Sonderfall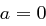 
ist zu beachten, hier setzen wir 
.
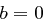2. Transformation.
Hier interpretieren wir das Byte nicht mehr als Polynom, sondern als Vektor über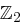 
. Auf das Ergebnis der ersten Transformation wenden wir die affine Transformation
ab und erhalten das Byte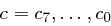 
, welches das Ergebnis der SubBytes Transformation ist. Beide Umwandlungen sind invertierbar, folglich kann man die Umkehroperation InvSubBytes definieren.
Bei der ShiftRows Transformation wird die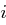 
-te Zeile des State um 
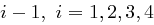, Positionen zyklisch nach links verschoben. Im Detail ändert sich der State wie folgt
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
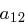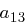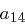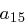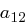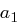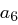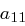Offensichtlich ist ShiftRows ebenfalls invertierbar, InvShiftRows muss die zyklischen Rotationen nur in die andere Richtung durchführen.
Bei der MixColumns-Transformation wird jeder Spalte eines State eine neue Spalte zugeordnet, wobei diese Zuordnung unabhängig von den anderen Spalten erfolgt. Genauer gesagt, stellen die Spalten des State jetzt Polynome dar, mit den einzelnen Einträgen als Koeffizienten:
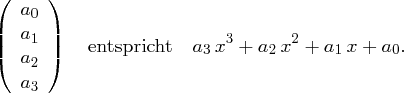
Im Gegensatz zur SubBytes-Transformation, bei denen die Koeffizienten und die Variable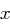 
einzelnen Bits entsprachen, haben wir es hier mit Polynomen vom Höchstgrad drei auf 
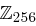zu tun. Um zu vermeiden, dass Polynome vom Grad vier (oder höher) auftreten, erfolgen sämtliche Berechnungen modulo des Reduktionspolynoms 
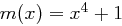. Im Zuge der MixColumns-Operation wird jede Spalte (also jedes der vier Polynome eines State) mit 
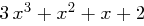multipliziert. Dabei entspricht die Multiplikation einzelner Zahlen (Bytes) der schon bei SubBytes besprochenen Polynommultiplikation - wir gehen wieder von Polynomen auf 
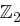mit Grad sieben aus.
Die Transformation einer Spalte können wir als Matrixmultiplikation auffassen:
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
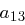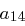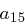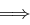
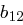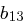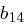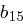Die Umkehroperation InvMixColumns multipliziert entsprechend jede Spalte des State mit dem zu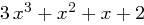 
inversen Polynom.
Bei dieser Operation wird der Rundenschlüssel mit dem State bitweise per XOR verknüpft.
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
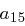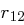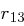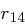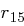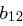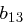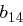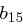Die Länge des Rundenschlüssels entspricht der verwendeten Blocklänge. Die Umkehroperation entspricht einfach der erneuten Anwendung der Schlüsseladdition, denn für zwei Bits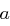 
und 
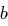gilt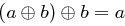 
; bei der Entschlüsselung werden die Rundenschlüssel einfach in umgekehrter Reihenfolge angewendet. Die Bestimmung dieser round keys werden wir im Folgenden kennenlernen.
Die einzelnen Rundenschlüssel werden aus dem expandierten Eingangsschlüssel abgeleitet, schließlich muss der jeweilige State in jeder Runde eine Schlüsseladdition erfahren (Round Key Addition). Dabei soll immer ein anderer Rundenschlüssel zum Einsatz kommen. Wir müssen also unseren Ursprungsschlüssel um soviele Spalten erweitern, wie nötig sind, um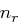 
Schlüsseladditionen durchzuführen. Der erweiterte Eingangsschlüssel ist also letztlich ein eindimensionales Feld, dessen Länge (das heißt, die Anzahl seiner Bits) sich berechnet durch
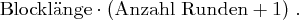
Legen wir die beiden Werte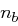 
und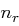 
zugrunde, dann besteht der erweiterte Eingangsschlüssel aus
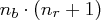
Worten mit je vier Byte. Die Betrachtung von jeweils 32 Bit, welche in einem Wort zusammengefasst sind, erweist sich bei der Beschreibung der Schlüsselerweiterung als günstiger. Die ersten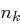 
Worte des erweiterten Schlüssels sind dabei die Worte des gegebenen Schlüssels, die ersten 
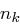Spalten werden also einfach kopiert. Alle weiteren Worte 
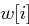berechnen sich rekursiv durch
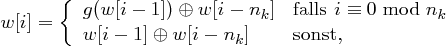
wobei für die Funktion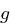 
gilt
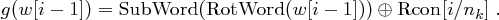
Die RotWord-Transformation.
Bei der RotWord-Transformation werden die 4 Bytes eines Wortes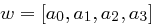 
zyklisch um eine Position nach links verschoben: 
.
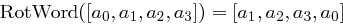Die SubWord-Transformation.
Bei der SubWord-Transformation wird auf jedes der 4 Bytes eines Wortes die Transformation SubBytes angewendet.
Die Rundenkonstante Rcon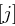
.
Für die Rundenkonstante Rcon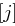
gilt Rcon
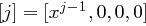, wobei 
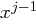die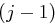 
-te Potenz von 
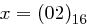(in anderen Worten, des Polynoms 
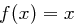) und 
das Nullbyte ist.
Aufgabe 1
Wir wollen modulo bestimmter Polynome wie in Restklassenringen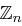 
rechnen.
Bestimmen Sie alle Polynome modulo des Polynoms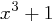 
mit Koeffizienten aus 
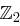, also alle Polynome 
.
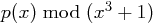Berechnen Sie über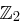 
:
