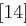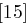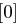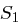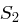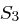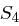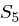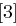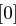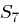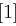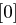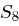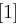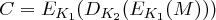DES - Data Encryption Standard
Verschlüsselung
Entschlüsselung
Übungen
Das Verschlüsselungsverfahren DES wurde von IBM im Auftrag der US-Regierung entwickelt und 1977 zum Verschlüsselungsstandard für nicht geheime Nachrichten.
Verschlüsselung
Beim DES-Verfahren werden 64 Bit lange Klartextblöcke in Kryptogrammblöcke gleicher Länge verschlüsselt. Der zur Verschlüsselung verwendete Schlüssel besteht zur Laufzeit ebenfalls aus 64 Bit. Tatsächlich stehen jedoch nur 56 Bit zur Verfügung, da das achte Bit eines Schlüsselbytes ein Paritätsbit ist, wobei dieses stets so gesetzt ist, dass die Anzahl Einsen gerade ist.
Bevor mit dem Verschlüsseln begonnen wird, erfolgt eine Eingangspermutation des 64-Bit-Klartextblocks entsprechend Tabelle 1.1.
| 58 |
50 |
42 |
34 |
26 |
18 |
10 |
2 |
| 60 |
52 |
44 |
36 |
28 |
20 |
12 |
4 |
| 62 |
54 |
46 |
38 |
30 |
22 |
14 |
6 |
| 64 |
56 |
48 |
40 |
32 |
24 |
16 |
8 |
| 57 |
49 |
41 |
33 |
25 |
17 |
9 |
1 |
| 59 |
51 |
43 |
35 |
27 |
19 |
11 |
3 |
| 61 |
53 |
45 |
37 |
29 |
21 |
13 |
5 |
| 63 |
55 |
47 |
39 |
31 |
23 |
15 |
7 |
|
|
| Tabelle 1.1: |
Eingangspermutation |
|
| 40 |
8 |
48 |
16 |
56 |
24 |
64 |
32 |
| 39 |
7 |
47 |
15 |
55 |
23 |
63 |
31 |
| 38 |
6 |
46 |
14 |
54 |
22 |
62 |
30 |
| 37 |
5 |
45 |
13 |
53 |
21 |
61 |
29 |
| 36 |
4 |
44 |
12 |
52 |
20 |
60 |
28 |
| 35 |
3 |
43 |
11 |
51 |
19 |
59 |
27 |
| 34 |
2 |
42 |
10 |
50 |
18 |
58 |
26 |
| 33 |
1 |
41 |
9 |
49 |
17 |
57 |
25 |
|
|
| Tabelle 1.2: |
Ausgangspermutation |
|
Anschließend erfolgt eine auf 16 Runden aufgeteilte Verarbeitung. Der 64-Bit-Block wird zunächst in eine linke Hälfte 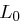 und eine rechte Hälfte
und eine rechte Hälfte 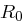 mit jeweils 32 Bit geteilt. In jeder der
mit jeweils 32 Bit geteilt. In jeder der 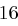 Runden wird die rechte Hälfte unverändert als linke Hälfte der nächsten Runde übernommen. Auf die rechte Seite einer Runde und einen speziellen Rundenschlüssel
Runden wird die rechte Hälfte unverändert als linke Hälfte der nächsten Runde übernommen. Auf die rechte Seite einer Runde und einen speziellen Rundenschlüssel  (dessen Erläuterung noch folgt) wird eine Funktion
(dessen Erläuterung noch folgt) wird eine Funktion 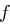 angewendet. Das Ergebnis dieser Funktion wird dann durch XOR mit der linken Hälfte der vorherigen Runde verknüpft:
angewendet. Das Ergebnis dieser Funktion wird dann durch XOR mit der linken Hälfte der vorherigen Runde verknüpft:
Chiffren, die nach diesem Prinzip verschlüsseln, nennt man übrigens Feistel-Chiffren. Nach Abschluss der 16 Runden wird noch die Ausgangspermutation entsprechend Tabelle 1.2 durchgeführt.
Erzeugung der Rundenschlüssel.
Die Eingabe für diesen Schritt ist der 64 Bit lange Schlüssel. Zunächst werden die relevanten 56 Bit des Schlüssels durch eine Schlüsselpermutation entsprechend Tabelle 1.3 von den Paritätsbits getrennt - die Tabelle enthält nur sieben Spalten mit je acht Einträgen, wobei sämtliche Vielfache von Acht (eben die Indizes der Paritätsbits) herausgefiltert werden. Der Begriff Permutation hat trotzdem eine gewisse Berechtigung, schließlich kann man diese Abbildung als Permutation betrachten, bei der bestimmte Bits in der letzten Spalte landen, die dann weggelassen wird.
| 57 |
49 |
41 |
33 |
25 |
17 |
9 |
| 1 |
58 |
50 |
42 |
34 |
26 |
18 |
| 10 |
2 |
59 |
51 |
43 |
35 |
27 |
| 19 |
11 |
3 |
60 |
52 |
44 |
36 |
| 63 |
55 |
47 |
39 |
31 |
23 |
15 |
| 7 |
62 |
54 |
46 |
38 |
30 |
22 |
| 14 |
6 |
61 |
53 |
45 |
37 |
29 |
| 21 |
13 |
5 |
28 |
20 |
12 |
4 |
|
|
| Tabelle 1.3: |
Schlüsselpermutation |
|
Die Blocklänge bei Schlüsseln beträgt also 56 Bit. Analog zu den Klartextblöcken unterscheiden wir auch hier eine linke Hälfte 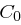 und eine rechte Hälfte
und eine rechte Hälfte 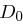 mit jeweils 28 Bit. In der
mit jeweils 28 Bit. In der 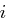 -ten Runde werden neue Schlüsselblöcke
-ten Runde werden neue Schlüsselblöcke 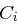 und
und 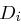 berechnet, indem
berechnet, indem 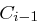 und
und 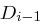 jeweils um ein oder zwei Bits (siehe Tabelle 1.4) zyklisch nach links verschoben werden. Insgesamt werden 28 Verschiebeoperationen durchgeführt, so dass die Blöcke am Ende wieder in ihrem Ausgangszustand sind.
jeweils um ein oder zwei Bits (siehe Tabelle 1.4) zyklisch nach links verschoben werden. Insgesamt werden 28 Verschiebeoperationen durchgeführt, so dass die Blöcke am Ende wieder in ihrem Ausgangszustand sind.
| Runde |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| Anzahl |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
|
|
| Tabelle 1.4: |
Schlüsselverschiebungen |
|
In Runde 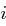 wird nun der Rundenschlüssel
wird nun der Rundenschlüssel 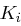 berechnet, indem die beiden Hälften
berechnet, indem die beiden Hälften 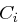 und
und 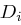 konkateniert werden (wir erhalten einen Block von 56 Bits) und anschließend die Kompressionspermutation entsprechend Tabelle 1.5 durchlaufen (hier werden wieder acht Bits weggelassen). Der Rundenschlüssel
konkateniert werden (wir erhalten einen Block von 56 Bits) und anschließend die Kompressionspermutation entsprechend Tabelle 1.5 durchlaufen (hier werden wieder acht Bits weggelassen). Der Rundenschlüssel 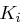 besteht somit aus 48 Bit.
besteht somit aus 48 Bit.
| 14 |
17 |
11 |
24 |
1 |
5 |
| 3 |
28 |
15 |
6 |
21 |
10 |
| 23 |
19 |
12 |
4 |
26 |
8 |
| 16 |
7 |
27 |
20 |
13 |
2 |
| 41 |
52 |
31 |
37 |
47 |
55 |
| 30 |
40 |
51 |
45 |
33 |
48 |
| 44 |
49 |
39 |
56 |
34 |
53 |
| 46 |
42 |
50 |
36 |
29 |
32 |
|
|
| Tabelle 1.5: |
Kompressionspermutation |
|
Spezifizierung der Funktion 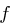 .
.
Auf den 48 Bit langen Rundenschlüssel 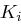 und die 32 Bit lange rechte Hälfte
und die 32 Bit lange rechte Hälfte 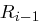 des Datenblocks wird die Funktion
des Datenblocks wird die Funktion 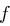 angewendet, die wir an dieser Stelle genauer erörtern wollen. Zunächst durchläuft der Block
angewendet, die wir an dieser Stelle genauer erörtern wollen. Zunächst durchläuft der Block 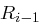 eine Expansionspermutation entsprechend Tabelle 1.6.
eine Expansionspermutation entsprechend Tabelle 1.6.
| 32 |
1 |
2 |
3 |
4 |
5 |
| 4 |
5 |
6 |
7 |
8 |
9 |
| 8 |
9 |
10 |
11 |
12 |
13 |
| 12 |
13 |
14 |
15 |
16 |
17 |
| 16 |
17 |
18 |
19 |
20 |
21 |
| 20 |
21 |
22 |
23 |
24 |
25 |
| 24 |
25 |
26 |
27 |
28 |
29 |
| 28 |
29 |
30 |
31 |
32 |
1 |
|
|
| Tabelle 1.6: |
Expansionspermutation |
|
Durch die Expansionspermutation wird der 32-Bit-Block 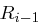 auf 48 Bit aufgeweitet (dies erreicht man durch Duplizieren einzelner Bits) und kann nun mit dem ebenfalls 48 Bit langen Rundenschlüssel
auf 48 Bit aufgeweitet (dies erreicht man durch Duplizieren einzelner Bits) und kann nun mit dem ebenfalls 48 Bit langen Rundenschlüssel 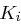 mittels XOR verknüpft werden. Die nun folgende S-Box-Transformation (Tabelle 1.8) ist der für die Sicherheit von DES wichtigste Bestandteil. Die durch die XOR-Verknüpfung entstandenen 48 Bit werden in acht Blöcke zu jeweils 6 Bit aufgeteilt, je ein Block als Eingabe für eine S-Box (Substitution Box). Das jeweils erste und letzte Bit eines solchen Blockes wird als Zahl interpretiert und bestimmt die Zeile in der dazugehörigen S-Box. Die durch Bits 2 bis 5 dargestellte Zahl bestimmt die Spalte der S-Box. Der so bestimmte Eintrag der S-Box ist eine Zahl zwischen 0 und 15 und wird als Binärzahl interpretiert. Alle S-Boxen zusammen liefern ein 32 Bit langes Wort, welches nun noch eine P-Box Permutation durchläuft, die in Tabelle 1.7 dargestellt ist.
mittels XOR verknüpft werden. Die nun folgende S-Box-Transformation (Tabelle 1.8) ist der für die Sicherheit von DES wichtigste Bestandteil. Die durch die XOR-Verknüpfung entstandenen 48 Bit werden in acht Blöcke zu jeweils 6 Bit aufgeteilt, je ein Block als Eingabe für eine S-Box (Substitution Box). Das jeweils erste und letzte Bit eines solchen Blockes wird als Zahl interpretiert und bestimmt die Zeile in der dazugehörigen S-Box. Die durch Bits 2 bis 5 dargestellte Zahl bestimmt die Spalte der S-Box. Der so bestimmte Eintrag der S-Box ist eine Zahl zwischen 0 und 15 und wird als Binärzahl interpretiert. Alle S-Boxen zusammen liefern ein 32 Bit langes Wort, welches nun noch eine P-Box Permutation durchläuft, die in Tabelle 1.7 dargestellt ist.
| 16 |
7 |
20 |
21 |
29 |
12 |
28 |
17 |
| 1 |
15 |
23 |
26 |
5 |
18 |
31 |
10 |
| 2 |
8 |
24 |
14 |
32 |
27 |
3 |
9 |
| 19 |
13 |
30 |
6 |
22 |
11 |
4 |
25 |
|
|
| Tabelle 1.7: |
P-Box Permutation |
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
 |
|
|
14 |
4 |
13 |
1 |
2 |
15 |
11 |
8 |
3 |
10 |
6 |
12 |
5 |
9 |
0 |
7 |
 |
 |
|
|
0 |
15 |
7 |
4 |
14 |
2 |
13 |
1 |
10 |
6 |
12 |
11 |
9 |
5 |
3 |
8 |
|
|
 |
|
|
4 |
1 |
14 |
8 |
13 |
6 |
2 |
11 |
15 |
12 |
9 |
7 |
3 |
10 |
5 |
0 |
|
|
 |
|
|
15 |
12 |
8 |
2 |
4 |
9 |
1 |
7 |
5 |
11 |
3 |
14 |
10 |
0 |
6 |
13 |
|
|
|
|
|
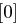 |
|
|
15 |
1 |
8 |
14 |
6 |
11 |
3 |
4 |
9 |
7 |
2 |
13 |
12 |
0 |
5 |
10 |
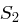 |
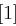 |
|
|
3 |
13 |
4 |
7 |
15 |
2 |
8 |
14 |
12 |
0 |
1 |
10 |
6 |
9 |
11 |
5 |
|
|
 |
|
|
0 |
14 |
7 |
11 |
10 |
4 |
13 |
1 |
5 |
8 |
12 |
6 |
9 |
3 |
2 |
15 |
|
|
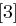 |
|
|
13 |
8 |
10 |
1 |
3 |
15 |
4 |
2 |
11 |
6 |
7 |
12 |
0 |
5 |
14 |
9 |
|
|
|
|
|
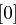 |
|
|
10 |
0 |
9 |
14 |
6 |
3 |
15 |
5 |
1 |
13 |
12 |
7 |
11 |
4 |
2 |
8 |
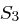 |
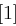 |
|
|
13 |
7 |
0 |
9 |
3 |
4 |
6 |
10 |
2 |
8 |
5 |
14 |
12 |
11 |
15 |
1 |
|
|
 |
|
|
13 |
6 |
4 |
9 |
8 |
15 |
3 |
0 |
11 |
1 |
2 |
12 |
5 |
10 |
14 |
7 |
|
|
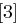 |
|
|
1 |
10 |
13 |
0 |
6 |
9 |
8 |
7 |
4 |
15 |
14 |
3 |
11 |
5 |
2 |
12 |
|
|
|
|
|
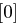 |
|
|
7 |
13 |
14 |
3 |
0 |
6 |
9 |
10 |
1 |
2 |
8 |
5 |
11 |
12 |
4 |
15 |
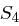 |
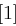 |
|
|
13 |
8 |
11 |
5 |
6 |
15 |
0 |
3 |
4 |
7 |
2 |
12 |
1 |
10 |
14 |
9 |
|
|
 |
|
|
10 |
6 |
9 |
0 |
12 |
11 |
7 |
13 |
15 |
1 |
3 |
14 |
5 |
2 |
8 |
4 |
|
|
 |
|
|
3 |
15 |
0 |
6 |
10 |
1 |
13 |
8 |
9 |
4 |
5 |
11 |
12 |
7 |
2 |
14 |
|
|
|
|
|
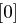 |
|
|
2 |
12 |
4 |
1 |
7 |
10 |
11 |
6 |
8 |
5 |
3 |
15 |
13 |
0 |
14 |
9 |
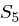 |
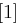 |
|
|
14 |
11 |
2 |
12 |
4 |
7 |
13 |
1 |
5 |
0 |
15 |
10 |
3 |
9 |
8 |
6 |
|
|
 |
|
|
4 |
2 |
1 |
11 |
10 |
13 |
7 |
8 |
15 |
9 |
12 |
5 |
6 |
3 |
0 |
14 |
|
|
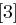 |
|
|
11 |
8 |
12 |
7 |
1 |
14 |
2 |
13 |
6 |
15 |
0 |
9 |
10 |
4 |
5 |
3 |
|
|
|
|
|
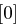 |
|
|
12 |
1 |
10 |
15 |
9 |
2 |
6 |
8 |
0 |
13 |
3 |
4 |
14 |
7 |
5 |
11 |
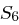 |
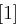 |
|
|
10 |
15 |
4 |
2 |
7 |
12 |
9 |
5 |
6 |
1 |
13 |
14 |
0 |
11 |
3 |
8 |
|
|
 |
|
|
9 |
14 |
15 |
5 |
2 |
8 |
12 |
3 |
7 |
0 |
4 |
10 |
1 |
13 |
11 |
6 |
|
|
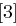 |
|
|
4 |
3 |
2 |
12 |
9 |
5 |
15 |
10 |
11 |
14 |
1 |
7 |
6 |
0 |
8 |
13 |
|
|
|
|
|
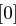 |
|
|
4 |
11 |
2 |
14 |
15 |
0 |
8 |
13 |
3 |
12 |
9 |
7 |
5 |
10 |
6 |
1 |
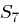 |
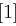 |
|
|
13 |
0 |
11 |
7 |
4 |
9 |
1 |
10 |
14 |
3 |
5 |
12 |
2 |
15 |
8 |
6 |
|
|
 |
|
|
1 |
4 |
11 |
13 |
12 |
3 |
7 |
14 |
10 |
15 |
6 |
8 |
0 |
5 |
9 |
2 |
|
|
 |
|
|
6 |
11 |
13 |
8 |
1 |
4 |
10 |
7 |
9 |
5 |
0 |
15 |
14 |
2 |
3 |
12 |
|
|
|
|
|
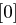 |
|
|
13 |
2 |
8 |
4 |
6 |
15 |
11 |
1 |
10 |
9 |
3 |
14 |
5 |
0 |
12 |
7 |
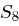 |
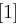 |
|
|
1 |
15 |
13 |
8 |
10 |
3 |
7 |
4 |
12 |
5 |
6 |
11 |
0 |
14 |
9 |
2 |
|
|
 |
|
|
7 |
11 |
4 |
1 |
9 |
12 |
14 |
2 |
0 |
6 |
10 |
13 |
15 |
3 |
5 |
8 |
|
|
 |
|
|
2 |
1 |
14 |
7 |
4 |
10 |
8 |
13 |
15 |
12 |
9 |
0 |
3 |
5 |
6 |
11 |
|
|
| Tabelle 1.8: |
S-Boxen  |
|
Entschlüsselung
Die Entschlüsselung entspricht der Verschlüsselung mit dem Unterschied, dass die Rundenschlüssel in umgekehrter Reihenfolge angewendet werden.
Übungen
Aufgabe 1
Zeigen Sie am Beispiel einer der S-Boxen von DES, dass diese nichtlinear ist.
Aufgabe 2
Zeigen Sie, dass das Vertauschen der linken und rechten Hälfte der 64-Bit-Blöcke nach jeder Runde eine lineare Operation ist.
Aufgabe 3
Die S-Boxen von DES sind das einzige nichtlineare Element von DES, worauf die Sicherheit basiert. Warum wäre DES mit linearen S-Boxen unsicher? Beschreiben Sie einen Angriff gegen ein derartiges lineares DES.
Aufgabe 4
Bestimmen Sie alle schwachen DES-Schlüssel.
Aufgabe 5
Berechnen Sie den Aufwand zum Brechen von Triple-DES
mit einem Meet-in-the-Middle-Angriff und vergleichen Sie diesen mit dem Aufwand zum Brechen von einfachem und doppeltem DES.
Link zu den Lösungen
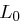 und eine rechte Hälfte
und eine rechte Hälfte 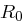 mit jeweils 32 Bit geteilt. In jeder der
mit jeweils 32 Bit geteilt. In jeder der 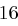 Runden wird die rechte Hälfte unverändert als linke Hälfte der nächsten Runde übernommen. Auf die rechte Seite einer Runde und einen speziellen Rundenschlüssel
Runden wird die rechte Hälfte unverändert als linke Hälfte der nächsten Runde übernommen. Auf die rechte Seite einer Runde und einen speziellen Rundenschlüssel  (dessen Erläuterung noch folgt) wird eine Funktion
(dessen Erläuterung noch folgt) wird eine Funktion 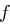 angewendet. Das Ergebnis dieser Funktion wird dann durch XOR mit der linken Hälfte der vorherigen Runde verknüpft:
angewendet. Das Ergebnis dieser Funktion wird dann durch XOR mit der linken Hälfte der vorherigen Runde verknüpft: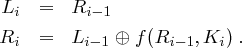
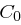 und eine rechte Hälfte
und eine rechte Hälfte 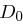 mit jeweils 28 Bit. In der
mit jeweils 28 Bit. In der 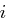 -ten Runde werden neue Schlüsselblöcke
-ten Runde werden neue Schlüsselblöcke 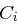 und
und 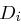 berechnet, indem
berechnet, indem 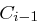 und
und 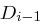 jeweils um ein oder zwei Bits (siehe Tabelle
jeweils um ein oder zwei Bits (siehe Tabelle 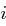 wird nun der Rundenschlüssel
wird nun der Rundenschlüssel 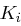 berechnet, indem die beiden Hälften
berechnet, indem die beiden Hälften 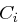 und
und 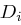 konkateniert werden (wir erhalten einen Block von 56 Bits) und anschließend die Kompressionspermutation entsprechend Tabelle
konkateniert werden (wir erhalten einen Block von 56 Bits) und anschließend die Kompressionspermutation entsprechend Tabelle 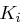 besteht somit aus 48 Bit.
besteht somit aus 48 Bit.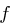
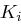 und die 32 Bit lange rechte Hälfte
und die 32 Bit lange rechte Hälfte 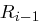 des Datenblocks wird die Funktion
des Datenblocks wird die Funktion 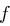 angewendet, die wir an dieser Stelle genauer erörtern wollen. Zunächst durchläuft der Block
angewendet, die wir an dieser Stelle genauer erörtern wollen. Zunächst durchläuft der Block 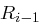 eine Expansionspermutation entsprechend Tabelle
eine Expansionspermutation entsprechend Tabelle 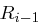 auf 48 Bit aufgeweitet (dies erreicht man durch Duplizieren einzelner Bits) und kann nun mit dem ebenfalls 48 Bit langen Rundenschlüssel
auf 48 Bit aufgeweitet (dies erreicht man durch Duplizieren einzelner Bits) und kann nun mit dem ebenfalls 48 Bit langen Rundenschlüssel 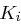 mittels XOR verknüpft werden. Die nun folgende S-Box-Transformation (Tabelle
mittels XOR verknüpft werden. Die nun folgende S-Box-Transformation (Tabelle