Bloms Schema
Eine Möglichkeit der Schlüsselverteilung ist Bloms Schema. Bei einem Schema für 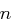 User sind die Schlüssel aus der Menge
User sind die Schlüssel aus der Menge 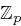 , wobei
, wobei 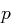 eine öffentlich bekannte Primzahl ist, für die
eine öffentlich bekannte Primzahl ist, für die 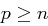 gilt. Weiterhin gibt es einen Sicherheitsparameter
gilt. Weiterhin gibt es einen Sicherheitsparameter 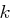 , der die größte Anzahl Teilnehmer einer Koalition angibt (damit ist gemeint, dass
, der die größte Anzahl Teilnehmer einer Koalition angibt (damit ist gemeint, dass 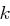 Personen untereinander Informationen austauschen können), so dass das Schema noch sicher ist. Mögliche Werte für diesen Parameter liegen in der Menge
Personen untereinander Informationen austauschen können), so dass das Schema noch sicher ist. Mögliche Werte für diesen Parameter liegen in der Menge 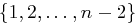 .
.
Das Schema funktioniert nun wie folgt.
Für jeden User 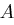 gibt es eine öffentliche Zahl
gibt es eine öffentliche Zahl 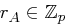 , wobei je zwei User verschiedene öffentliche Zahlen besitzen. Ein Trust Center wählt nun zufällig Zahlen
, wobei je zwei User verschiedene öffentliche Zahlen besitzen. Ein Trust Center wählt nun zufällig Zahlen 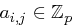 ,
, 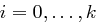 und
und 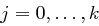 , mit
, mit 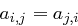 für
für 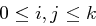 , die das folgende Polynom in den Variablen
, die das folgende Polynom in den Variablen 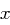 und
und 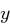 bestimmen
bestimmen
Für jeden User 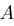 berechnet das Trust Center in
berechnet das Trust Center in 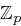 ein Polynom
ein Polynom
und sendet dem User 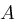 das Polynom
das Polynom 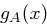 über einen sicheren Kanal.
über einen sicheren Kanal.
Falls die User 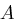 und
und 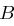 kommunizieren wollen, berechnen sie jeweils
kommunizieren wollen, berechnen sie jeweils 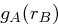 und
und 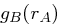 und erhalten den Kommunikationsschlüssel
und erhalten den Kommunikationsschlüssel
Der Vorteil bei Bloms Schema ist, dass jeder User A je nach Sicherheitsparameter nur 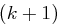 Elemente aus
Elemente aus 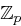 speichern muss, nämlich die Koeffizienten des Polynoms
speichern muss, nämlich die Koeffizienten des Polynoms 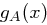 .
.
Lemma 15
Bloms Schema für 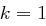 ist sicher bzgl. eines Angriffs jedes anderen einzelnen Users.
ist sicher bzgl. eines Angriffs jedes anderen einzelnen Users.
Beweis Das Trust Center habe die Funktion
gewählt.
Ein User 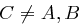 möchte den Kommunikationsschlüssel
möchte den Kommunikationsschlüssel 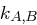 mit
mit
berechnen. Hierbei sind
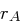
und
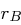
öffentlich bekannt, aber
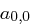
,
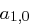
sowie
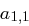
sind unbekannt.
Der Angreifer  kennt sein Polynom
kennt sein Polynom
und nimmt nun an, dass
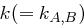
der Kommunikationsschlüssel von
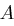
und
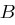
ist. Die Information, welche
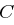
zur Verfügung steht, kann man mittels eines Gleichungssystems darstellen, bei dem
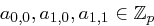
bestimmt werden sollen:
Wir betrachten die Determinante der Matrix:
dies folgt aus
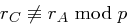
und
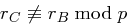
, da
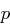
eine Primzahl ist. Da die Determinante ungleich Null ist, ist das Gleichungssystem für jeden angenommenen Schlüssel
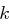
eindeutig nach
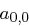
,
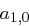
und
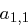
auflösbar. Der Schlüssel
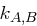
kann nicht von
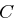
identifiziert werden.
Zwei User 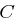 und
und 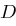 in einer Koalition können jedoch den Schlüssel
in einer Koalition können jedoch den Schlüssel 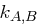 für
für 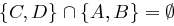 berechnen. Sie kennen nämlich
berechnen. Sie kennen nämlich
Aus (1.1) und (1.3) folgt
also mit 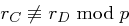 :
:
Damit lässt sich 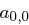 mit (1.1) oder (1.3) leicht berechnen. Analog erhält man aus (1.2) und (1.4) den Wert von
mit (1.1) oder (1.3) leicht berechnen. Analog erhält man aus (1.2) und (1.4) den Wert von 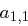 , damit kennen
, damit kennen 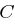 und
und 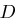 das geheime Polynom
das geheime Polynom 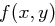 und können alle Schlüssel berechnen. Analog kann man zeigen:
und können alle Schlüssel berechnen. Analog kann man zeigen:
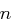 User sind die Schlüssel aus der Menge
User sind die Schlüssel aus der Menge 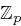 , wobei
, wobei 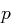 eine öffentlich bekannte Primzahl ist, für die
eine öffentlich bekannte Primzahl ist, für die 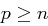 gilt. Weiterhin gibt es einen Sicherheitsparameter
gilt. Weiterhin gibt es einen Sicherheitsparameter 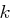 , der die größte Anzahl Teilnehmer einer Koalition angibt (damit ist gemeint, dass
, der die größte Anzahl Teilnehmer einer Koalition angibt (damit ist gemeint, dass 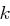 Personen untereinander Informationen austauschen können), so dass das Schema noch sicher ist. Mögliche Werte für diesen Parameter liegen in der Menge
Personen untereinander Informationen austauschen können), so dass das Schema noch sicher ist. Mögliche Werte für diesen Parameter liegen in der Menge 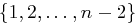 .
.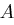 gibt es eine öffentliche Zahl
gibt es eine öffentliche Zahl 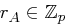 , wobei je zwei User verschiedene öffentliche Zahlen besitzen. Ein Trust Center wählt nun zufällig Zahlen
, wobei je zwei User verschiedene öffentliche Zahlen besitzen. Ein Trust Center wählt nun zufällig Zahlen 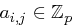 ,
, 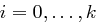 und
und 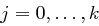 , mit
, mit 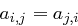 für
für 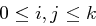 , die das folgende Polynom in den Variablen
, die das folgende Polynom in den Variablen 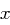 und
und 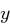 bestimmen
bestimmen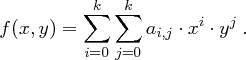
 berechnet das Trust Center in
berechnet das Trust Center in  ein Polynom
ein Polynom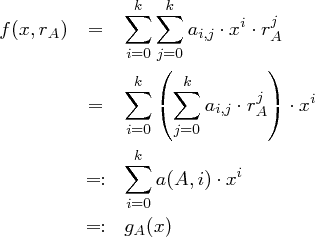
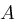 das Polynom
das Polynom 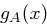 über einen sicheren Kanal.
über einen sicheren Kanal.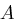 und
und 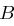 kommunizieren wollen, berechnen sie jeweils
kommunizieren wollen, berechnen sie jeweils 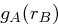 und
und 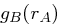 und erhalten den Kommunikationsschlüssel
und erhalten den Kommunikationsschlüssel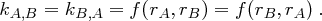
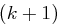 Elemente aus
Elemente aus 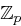 speichern muss, nämlich die Koeffizienten des Polynoms
speichern muss, nämlich die Koeffizienten des Polynoms 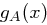 .
.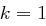 ist sicher bzgl. eines Angriffs jedes anderen einzelnen Users.
ist sicher bzgl. eines Angriffs jedes anderen einzelnen Users.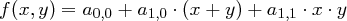
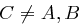 möchte den Kommunikationsschlüssel
möchte den Kommunikationsschlüssel 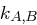 mit
mit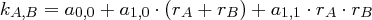
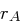 und
und 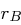 öffentlich bekannt, aber
öffentlich bekannt, aber 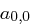 ,
, 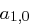 sowie
sowie 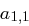 sind unbekannt.
sind unbekannt.
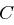 kennt sein Polynom
kennt sein Polynom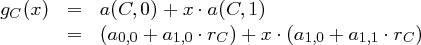
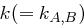 der Kommunikationsschlüssel von
der Kommunikationsschlüssel von 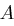 und
und 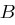 ist. Die Information, welche
ist. Die Information, welche 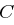 zur Verfügung steht, kann man mittels eines Gleichungssystems darstellen, bei dem
zur Verfügung steht, kann man mittels eines Gleichungssystems darstellen, bei dem 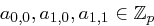 bestimmt werden sollen:
bestimmt werden sollen:

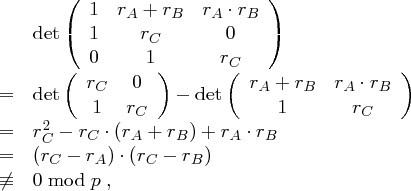
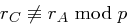 und
und 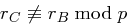 , da
, da 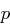 eine Primzahl ist. Da die Determinante ungleich Null ist, ist das Gleichungssystem für jeden angenommenen Schlüssel
eine Primzahl ist. Da die Determinante ungleich Null ist, ist das Gleichungssystem für jeden angenommenen Schlüssel 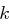 eindeutig nach
eindeutig nach 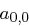 ,
, 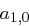 und
und 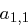 auflösbar. Der Schlüssel
auflösbar. Der Schlüssel 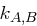 kann nicht von
kann nicht von 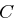 identifiziert werden.
identifiziert werden.
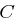 und
und 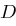 in einer Koalition können jedoch den Schlüssel
in einer Koalition können jedoch den Schlüssel 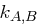 für
für 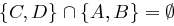 berechnen. Sie kennen nämlich
berechnen. Sie kennen nämlich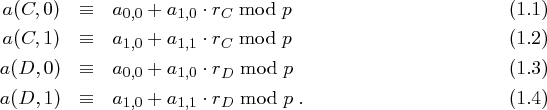
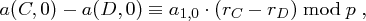
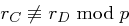 :
: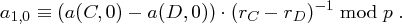
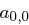 mit (
mit (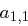 , damit kennen
, damit kennen 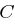 und
und 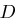 das geheime Polynom
das geheime Polynom 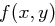 und können alle Schlüssel berechnen. Analog kann man zeigen:
und können alle Schlüssel berechnen. Analog kann man zeigen: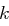 ist sicher bzgl. jeder Koalition von
ist sicher bzgl. jeder Koalition von 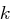 anderen Usern, aber unsicher bzgl. einer Koalition von
anderen Usern, aber unsicher bzgl. einer Koalition von 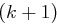 Usern.
Usern.