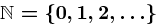
| Bloms Schema |
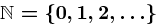 Ganze Zahlen
Ganze Zahlen 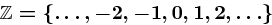
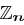 - Restklassenring modulo
- Restklassenring modulo 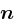 Übungen
Übungen
Im Folgenden werden einige für das Verständnis sinnvolle mathematische Definitionen und Sätze (teilweise mit Beweis) vorgestellt.
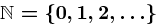
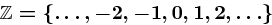
Definition 17 (Teilbarkeit)
Seien 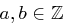 .
.
Man sagt "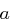 teilt
teilt 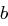 " (geschrieben:
" (geschrieben: 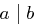 ), wenn es eine Zahl
), wenn es eine Zahl 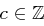 gibt, sodass
gibt, sodass 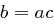 gilt. In diesem Fall heißen
gilt. In diesem Fall heißen 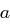 und
und  Teiler von
Teiler von 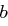 .
.
Definition 19 (Größter gemeinsamer Teiler)
Seien 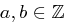 .
.
Eine Zahl 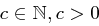 nennt man den größten gemeinsamen Teiler von
nennt man den größten gemeinsamen Teiler von 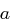 und
und 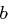 , wenn
, wenn 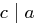 und
und 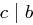 und keine Zahl
und keine Zahl 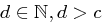 mit
mit 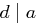 und
und 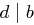 existiert. Man schreibt
existiert. Man schreibt 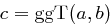 .
.
Bemerkung 20 (Eigenschaften des größten gemeinsamen Teilers)
Für 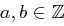 gilt
gilt
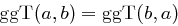
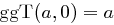 für
für 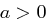
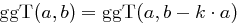 für alle
für alle 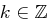
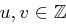 mit
mit 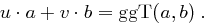
Satz 23 (Primfaktorenzerlegung)
Jede Zahl 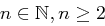 lässt sich eindeutig (bis auf die Reihenfolge) als Produkt von Primzahlpotenzen darstellen:
lässt sich eindeutig (bis auf die Reihenfolge) als Produkt von Primzahlpotenzen darstellen:
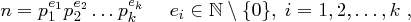
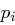 paarweise verschiedene Primzahlen sind.
paarweise verschiedene Primzahlen sind.
Definition 24 (Eulersche 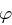 -Funktion)
-Funktion)
Sei 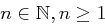 .
.
Dann bezeichnet 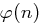 die Anzahl der Zahlen in
die Anzahl der Zahlen in 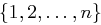 , die teilerfremd zu
, die teilerfremd zu 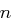 sind:
sind:
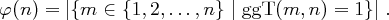
Satz 25 (Eigenschaften der Eulerschen 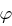 -Funktion)
-Funktion)
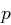 gilt
gilt 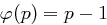 .
.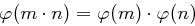 , falls
, falls 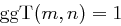 ist.
ist.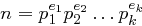 die Primfaktorenzerlegung von
die Primfaktorenzerlegung von 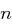 ist, dann gilt
ist, dann gilt
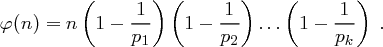

Die Korrektheit des Euklidischen Algorithmus basiert auf den in Bemerkung 20 genannten Eigenschaften des größten gemeinsamen Teilers in leicht veränderter Form: 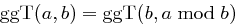 .
.

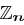 - Restklassenring modulo
- Restklassenring modulo 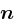
Definition 27 (Restklassenring modulo 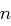 )
)
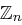 ist die Menge
ist die Menge  der natürlichen Zahlen. Addition, Subtraktion und Multiplikation in
der natürlichen Zahlen. Addition, Subtraktion und Multiplikation in 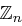 werden modulo
werden modulo 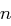 durchgeführt.
durchgeführt.
Definition 28 (Multiplikatives Inverses)
Sei 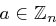 .
.
Das multiplikative Inverse von 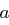 modulo
modulo 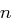 ist die Zahl
ist die Zahl 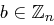 mit
mit 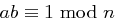 . Falls
. Falls 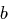 existiert, so ist es eindeutig und wird mit
existiert, so ist es eindeutig und wird mit 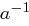 beschrieben;
beschrieben; 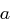 nennt man dann in
nennt man dann in 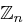 invertierbar.
invertierbar.
Definition 29 (Division in 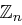 )
)
Seien 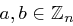 .
.
In 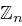 ist die Division von
ist die Division von 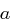 durch
durch 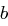 das Produkt von
das Produkt von 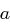 und
und 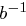 und nur definiert, falls
und nur definiert, falls 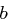 invertierbar in
invertierbar in  ist.
ist.
Aus Satz 30 folgt für 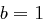 :
:
Satz 32 (Chinesischer Restsatz)
Seien 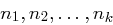 paarweise teilerfremd und
paarweise teilerfremd und 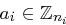 ,
, 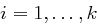 .
.
Dann hat das System
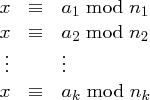
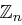 mit
mit 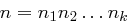 .
.
Beweis Wir definieren 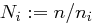 mit
mit 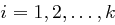 . Da die
. Da die 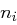 paarweise teilerfremd sind, ist
paarweise teilerfremd sind, ist
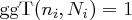
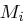 existieren mit
existieren mit
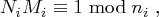
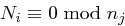 für
für 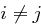 . Nun setzen wir
. Nun setzen wir
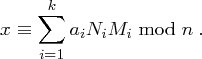
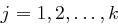 gilt unter der Voraussetzung
gilt unter der Voraussetzung 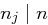 deshalb:
deshalb:
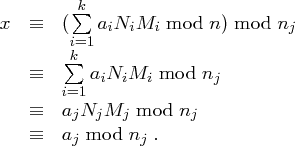
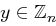 mit obigen Eigenschaften, so folgt
mit obigen Eigenschaften, so folgt 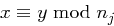 für
für 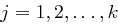 und aufgrund der paarweisen Teilerfremdheit der
und aufgrund der paarweisen Teilerfremdheit der 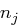 auch
auch 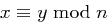 , d.h. unser
, d.h. unser 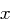 erfüllt alle Anforderungen und ist in
erfüllt alle Anforderungen und ist in 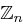 eindeutig.
eindeutig.
Definition 33 (Multiplikative Gruppe 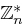 )
)
Die Menge der Zahlen aus 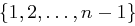 , die zu
, die zu 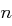 teilerfremd sind, bezeichnet man als
teilerfremd sind, bezeichnet man als 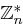 :
:
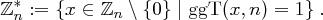
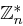 ist abgeschlossen bezüglich der Multiplikation in
ist abgeschlossen bezüglich der Multiplikation in 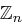 .
.
Definition 34 (Ordnung von 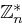 )
)
Die Ordnung von 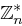 ist die Anzahl der Elemente in dieser Menge und es gilt nach Definition 24:
ist die Anzahl der Elemente in dieser Menge und es gilt nach Definition 24:
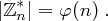
Definition 35 (Ordnung von 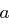 )
)
Sei 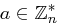 .
.
Unter der Ordnung von einem Element 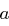 versteht man die kleinste Zahl
versteht man die kleinste Zahl 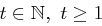 mit
mit 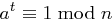 .
.
Definition 36 (Erzeugendes Element, zyklische Gruppe)
Sei 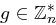 .
.
Falls die Ordnung eines Elements 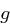 gleich
gleich 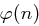 ist, so bezeichnet man
ist, so bezeichnet man 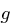 als ein erzeugendes (bzw. primitives) Element. Enthält
als ein erzeugendes (bzw. primitives) Element. Enthält 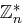 ein erzeugendes Element, dann nennt man die Gruppe zyklisch.
ein erzeugendes Element, dann nennt man die Gruppe zyklisch.
Satz 37 (Eigenschaften erzeugender Elemente)
Sei 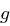 ein erzeugendes Element von
ein erzeugendes Element von 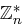 .
.
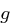 existiert genau dann, wenn
existiert genau dann, wenn 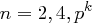 oder
oder 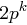 , wobei
, wobei 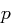 eine ungerade Primzahl und
eine ungerade Primzahl und 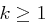 ist.
ist.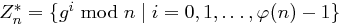
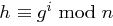 ist genau dann erzeugendes Element, wenn gilt
ist genau dann erzeugendes Element, wenn gilt 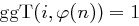 .
.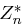 eine zyklische Gruppe ist, die Anzahl erzeugender Elemente gleich
eine zyklische Gruppe ist, die Anzahl erzeugender Elemente gleich 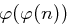 ist.
ist.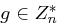 ist genau dann erzeugendes Element, wenn
ist genau dann erzeugendes Element, wenn 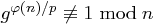 für jeden Primfaktor
für jeden Primfaktor 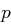 von
von 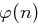 ist.
ist.Definition 38 (Diskreter Logarithmus)
Sei 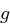 ein erzeugendes Element von
ein erzeugendes Element von 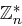 .
.
Dann gibt es zu jedem Element 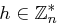 eine positive Zahl
eine positive Zahl 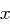 mit
mit 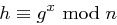 . Diese Zahl
. Diese Zahl 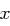 bezeichnet man als den diskreten Logarithmus von
bezeichnet man als den diskreten Logarithmus von 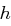 zur Basis
zur Basis 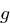 in
in 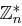 .
.
Beweis Zuerst zeigen wir, dass aus 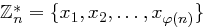 folgt
folgt 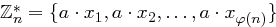 für
für 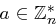 . Dies gilt, denn
. Dies gilt, denn
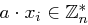 (folgt aus
(folgt aus 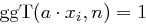 für
für 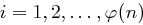 ) und
) und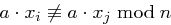 für
für 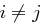 , denn aus
, denn aus 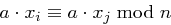 folgt sofort
folgt sofort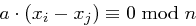 und mit
und mit 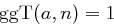 erhält man
erhält man 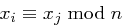 .
.Mit 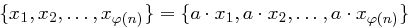 erhalten wir dann
erhalten wir dann
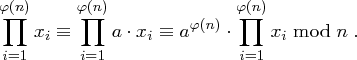
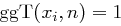 für
für 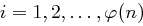 , gilt auch
, gilt auch 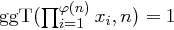 und es folgt mit Satz 31 die Behauptung
und es folgt mit Satz 31 die Behauptung 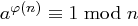 .
.
Bemerkung 42
Der Satz 41 ermöglicht es in manchen Fällen, die Lösung des Problems 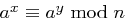 für
für 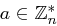 auf die Lösung des Problems
auf die Lösung des Problems 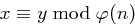 zurückzuführen.
zurückzuführen.
Beweis Falls 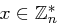 , so folgt die Behauptung aus Satz 41 und im Falle
, so folgt die Behauptung aus Satz 41 und im Falle 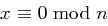 gilt sie trivialerweise. Damit bleiben die Möglichkeiten entweder
gilt sie trivialerweise. Damit bleiben die Möglichkeiten entweder 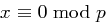 oder
oder 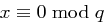 .
.
O.B.d.A. wollen wir den ersten Fall betrachten. Für 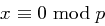 ist offenbar
ist offenbar 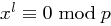 für jedes
für jedes 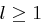 , also
, also 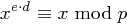 . Mit
. Mit 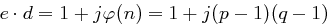 für ein
für ein 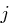 und Satz 25 ergibt sich folglich wegen
und Satz 25 ergibt sich folglich wegen 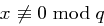 mit dem Satz von Euler
mit dem Satz von Euler
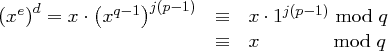
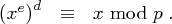
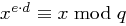 und
und 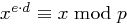 und, da
und, da 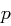 und
und 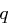 verschieden sind, also
verschieden sind, also 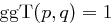 , ergibt sich somit die Behauptung
, ergibt sich somit die Behauptung 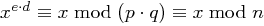 .
.
Satz 45 (Eulersches Kriterium, quadratischer Rest)
Sei 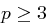 eine Primzahl und
eine Primzahl und 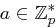 .
.
Die Kongruenz 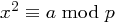 ist genau dann lösbar, wenn gilt
ist genau dann lösbar, wenn gilt
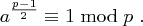
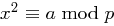 lösbar ist, so nennt man
lösbar ist, so nennt man 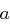 einen quadratischen Rest modulo p, andernfalls einen quadratischen Nichtrest modulo p.
einen quadratischen Rest modulo p, andernfalls einen quadratischen Nichtrest modulo p.
Beweis
" " Ist
" Ist 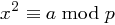 lösbar, und damit
lösbar, und damit 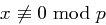 , dann gilt:
, dann gilt:
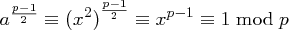
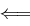 " Wir nehmen an, dass
" Wir nehmen an, dass 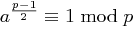 gilt. Die multiplikative Gruppe
gilt. Die multiplikative Gruppe 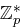 besitzt ein erzeugendes Element
besitzt ein erzeugendes Element 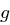 und, da
und, da 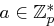 , gibt es eine natürliche Zahl
, gibt es eine natürliche Zahl 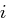 mit
mit 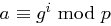 . Damit folgt
. Damit folgt
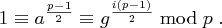
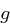 sei erzeugendes Element, liefern, dass
sei erzeugendes Element, liefern, dass 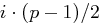 ein ganzzahliges Vielfaches von
ein ganzzahliges Vielfaches von 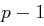 ist und damit
ist und damit 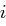 gerade sein muss, etwa
gerade sein muss, etwa 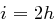 . Dies bedeutet aber
. Dies bedeutet aber 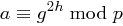 und für
und für 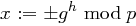 erhalten wir die Behauptung
erhalten wir die Behauptung 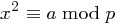 .
.
Satz 46
Sei 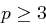 eine Primzahl.
eine Primzahl.
In 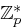 ist die Anzahl der quadratischen Reste gleich der Anzahl der quadratischen Nichtreste.
ist die Anzahl der quadratischen Reste gleich der Anzahl der quadratischen Nichtreste.
Beweis Die Behauptung folgt unmittelbar aus folgendem Lemma.
Lemma 47
Sei 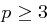 eine Primzahl.
eine Primzahl.
Für ein erzeugendes Element 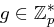 ist
ist 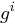 genau dann quadratischer Rest, wenn
genau dann quadratischer Rest, wenn 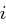 gerade ist.
gerade ist.
Beweis
"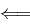 " Ist
" Ist 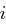 gerade, dann ist
gerade, dann ist 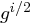 natürlich eine Quadratwurzel von
natürlich eine Quadratwurzel von 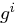 und somit
und somit 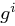 quadratischer Rest modulo
quadratischer Rest modulo 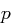 .
.
" " Sei nun
" Sei nun 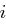 ungerade, d.h.
ungerade, d.h. 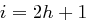 . Angenommen, es gibt ein
. Angenommen, es gibt ein 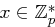 mit
mit 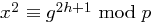 . Da
. Da 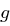 erzeugendes Element in
erzeugendes Element in 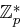 ist, muss ein
ist, muss ein 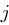 mit
mit 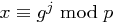 existieren. Also ist
existieren. Also ist 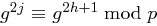 und nach Bemerkung 42 auch
und nach Bemerkung 42 auch 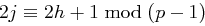 . Dies würde jedoch
. Dies würde jedoch 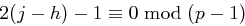 implizieren, aber da
implizieren, aber da 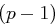 gerade und
gerade und 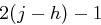 ungerade ist, erhalten wir mit der Annahme,
ungerade ist, erhalten wir mit der Annahme, 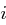 sei ungerade, einen Widerspruch.
sei ungerade, einen Widerspruch.
Aufgabe 1
Bestimmen Sie alle Parameter, für welche die Gleichung 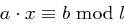 genau
genau 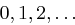 Lösungen hat.
Lösungen hat.
(Hinweis: Ist 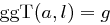 , so existieren ganze Zahlen
, so existieren ganze Zahlen 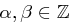 mit
mit 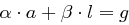 , vgl. Bemerkung 20 (iv).)
, vgl. Bemerkung 20 (iv).)
Aufgabe 2
Seien 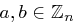 mit
mit 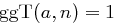 und
und 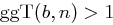 .
.
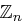 das multiplikative Inverse von
das multiplikative Inverse von 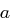 ?
?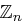 nicht das multiplikative Inverse von
nicht das multiplikative Inverse von 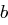 ?
?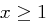 mit
mit 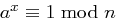 ?
?
Aufgabe 3
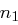 und
und 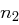 für die Eulersche
für die Eulersche 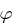 -Funktion gilt
-Funktion gilt
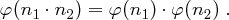
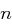 mit Primfaktorzerlegung
mit Primfaktorzerlegung 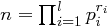 mit
mit 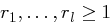 gilt:
gilt:
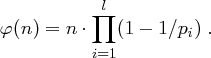
Aufgabe 4
Lösen Sie die beiden folgenden Systeme simultaner Kongruenzen:

Aufgabe 5
Gegeben ist eine zyklische Gruppe 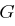 mit
mit 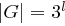 .
.
Wie kann man schnell entscheiden, welche Ordnung ein gegebenes Element hat?
Aufgabe 6
Sei 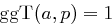 . Zeigen Sie, dass
. Zeigen Sie, dass 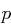 eine Primzahl ist, genau dann, wenn gilt
eine Primzahl ist, genau dann, wenn gilt
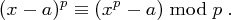
Aufgabe 7
Bestimmen Sie mit dem erweiterten Euklidischen Algorithmus die Inversen von
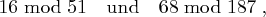
sofern diese existieren.
Aufgabe 8
Für genau welche Primzahlen 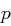 ist die Kongruenz
ist die Kongruenz 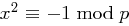 lösbar?
lösbar?
Aufgabe 9
Versuchen Sie in Analogie zum Eulerschen Kriterium ein hinreichendes und notwendiges Kriterium für die Lösbarkeit der Kongruenz 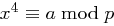 für Primzahlen
für Primzahlen 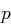 und
und 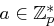 zu bestimmen und zu verifizieren.
zu bestimmen und zu verifizieren.
Aufgabe 10
Für 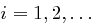 sei
sei 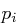 die
die 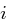 -te Primzahl. Begründen Sie, warum die (schlechte) obere Schranke
-te Primzahl. Begründen Sie, warum die (schlechte) obere Schranke 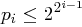 für alle
für alle 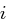 gilt.
gilt.
Aufgabe 11
Wie prüft man bei einer gegebenen 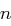 -stelligen Binärzahl algorithmisch in maximal
-stelligen Binärzahl algorithmisch in maximal 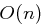 Schritten, ob diese durch
Schritten, ob diese durch  ,
, 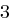 oder
oder 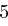 ohne Rest teilbar ist?
ohne Rest teilbar ist?
Aufgabe 12
Man weiß, dass für 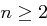 für die Anzahl
für die Anzahl 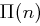 der Primzahlen kleiner gleich
der Primzahlen kleiner gleich 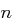 gilt
gilt
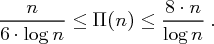
Zeigen Sie, dass für jede natürliche Zahl 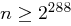 gilt:
gilt:
Zwischen 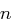 und
und 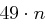 liegt immer eine Primzahl.
liegt immer eine Primzahl.
Aufgabe 13
Sei 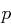 ein Primteiler von
ein Primteiler von 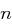 und
und 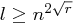 mit
mit 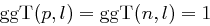 mit
mit
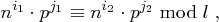
für verschiedene Paare 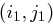 und
und 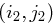 mit
mit 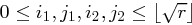 .
.
Zeigen Sie, dass dann 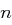 eine Potenz von
eine Potenz von 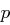 ist.
ist.