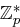 , auf dem das ElGamal Kryptosystem basiert. Hintergrund ist folgender:
, auf dem das ElGamal Kryptosystem basiert. Hintergrund ist folgender:| RSA | Pohlig-Hellman Algorithmus |
Die Sicherheit des RSA-Systems basiert darauf, dass Faktorisieren von natürlichen Zahlen wahrscheinlich algorithmisch schwierig ist, das bedeutet, es sind derzeit keine Polynomialzeitalgorithmen zur Lösung dieses Problems bekannt. Ein vermutlich ähnlich schweres Problem ist das des diskreten Logarithmus in 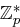 , auf dem das ElGamal Kryptosystem basiert. Hintergrund ist folgender:
, auf dem das ElGamal Kryptosystem basiert. Hintergrund ist folgender:
| Gegeben: | Ein Tripel 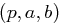 , wobei , wobei 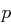 eine Primzahl und eine Primzahl und 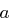 primitiv ist, also Erzeuger von primitiv ist, also Erzeuger von 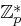 , , |
das heißt 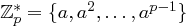 , und , und 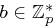 . . |
|
| Gesucht: | Ein 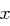 mit mit 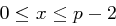 und und 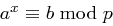 . . |
Für kryptographische Anwendungen sollte die Primzahl 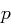 mindestens
mindestens 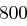 Bits haben, damit ein Angreifer nicht mit Brute Force Verfahren ein geeignetes
Bits haben, damit ein Angreifer nicht mit Brute Force Verfahren ein geeignetes 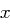 mit
mit 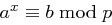 in vertretbarer Zeit finden kann.
in vertretbarer Zeit finden kann.
Alice möchte an Bob eine Nachricht senden. Beim ElGamal Kryptosystem ist das Tripel 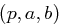 öffentlich, während
öffentlich, während 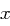 mit
mit 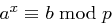 geheim ist. Zum Verschlüsseln einer Nachricht
geheim ist. Zum Verschlüsseln einer Nachricht 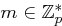 wählt Alice eine zufällige Zahl
wählt Alice eine zufällige Zahl 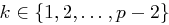 und berechnet
und berechnet
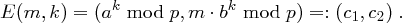
Zum Dechiffrieren wird von Bob
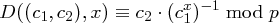
berechnet.
Man wählt nicht 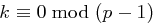 , da dann
, da dann 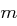 als Klartext übertragen wird.
als Klartext übertragen wird.
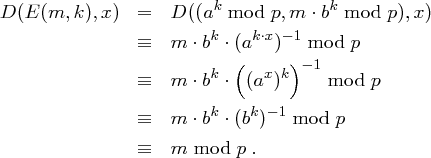
Das Chiffrat ist doppelt so lang wie der Klartext.
Wird zweimal der gleiche Exponent 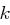 verwendet, so kann ein Angreifer, wenn er zwei Chiffrate
verwendet, so kann ein Angreifer, wenn er zwei Chiffrate 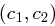 und
und 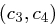 hat und die zu
hat und die zu 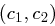 zugehörige Nachricht
zugehörige Nachricht 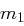 , auch die zu
, auch die zu 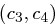 gehörige Nachricht
gehörige Nachricht 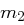 mit
mit 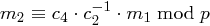 berechnen, denn wegen
berechnen, denn wegen 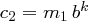 und
und 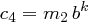 gilt
gilt 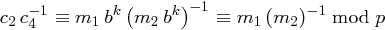 .
.