Gegeben: Ein Tripel
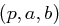 , wobei
, wobei 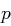 Primzahl ist,
Primzahl ist, 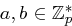 und
und 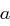 primitiv in
primitiv in 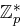 .
.Gesucht: Das
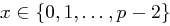 mit
mit 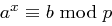 .
.| ElGamal | Digitale Signaturen |
Im vorangegangenen Abschnitt haben wir ein Kryptosystem betrachtet, dessen Sicherheit darauf beruht, dass das Diskrete Logarithmusproblem (DLP) schwierig ist, also auf der Annahme, dass es keine polynomiellen Lösungsverfahren gibt. Wir wollen nun versuchen, das DLP algorithmisch zu lösen.
Diskretes Logarithmusproblem (DLP)
Gegeben: Ein Tripel 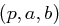 , wobei
, wobei 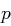 Primzahl ist,
Primzahl ist, 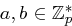 und
und 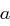 primitiv in
primitiv in 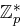 .
.
Gesucht: Das 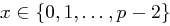 mit
mit 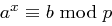 .
.
Trivialer Algorithmus
Für 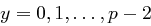 berechne
berechne 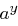 bis
bis 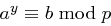 gilt, die Lösung ist dann
gilt, die Lösung ist dann 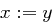 .
.
Die Anzahl der Multiplikationen bei diesem trivialen Algorithmus ist im worst case 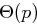 , also nicht polynomiell in der Eingabelänge
, also nicht polynomiell in der Eingabelänge 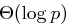 .
.
Der Pohlig-Hellman Algorithmus berechnet zu gegebenem Tripel 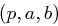 (
(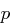 prim,
prim, 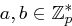 und
und 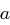 primitiv in
primitiv in 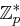 ) ein
) ein 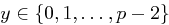 mit
mit 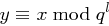 , wobei
, wobei 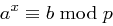 gilt und
gilt und 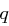 eine Primzahl ist mit
eine Primzahl ist mit 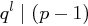 ,
, 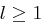 , aber
, aber 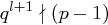 .
.
Kennt man alle paarweise verschiedenen Primteiler  von
von 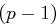 , also
, also 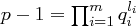 , so liefert das Pohlig-Hellman Verfahren Werte
, so liefert das Pohlig-Hellman Verfahren Werte 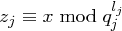 ,
, 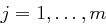 . Damit kann der Wert
. Damit kann der Wert 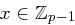 mit
mit 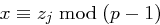 ,
, 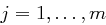 , mit dem Chinesischen Restsatz leicht berechnet werden, sodass gilt
, mit dem Chinesischen Restsatz leicht berechnet werden, sodass gilt 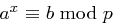 .
.
Bevor wir das Verfahren anwenden, machen wir zunächst einige Vorbemerkungen. Sei 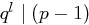 und
und 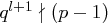 für eine Primzahl
für eine Primzahl 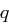 . Der gesuchte Wert
. Der gesuchte Wert 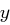 mit
mit 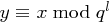 hat eine Darstellung der Form
hat eine Darstellung der Form
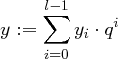
mit 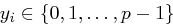 für
für 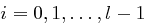 . Man berechnet nun sukzessive die Werte
. Man berechnet nun sukzessive die Werte 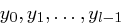 .
.
Beweis Aus 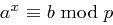 und
und 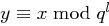 folgt die Existenz von
folgt die Existenz von 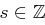 mit
mit 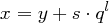 . Mit
. Mit 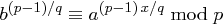 reicht es daher zu zeigen, dass gilt
reicht es daher zu zeigen, dass gilt
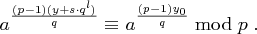
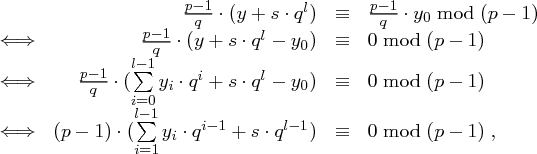
Beim Pohlig-Hellman Verfahren wird 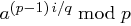 für
für 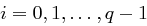 berechnet bis
berechnet bis 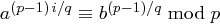 erfüllt ist, man setzt dann
erfüllt ist, man setzt dann 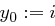 .
.
Für 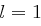 ist man fertig, sonst wird
ist man fertig, sonst wird 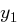 wie folgt berechnet: Sei
wie folgt berechnet: Sei 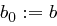 und setze
und setze 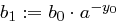 und
und 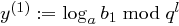 . Dann gilt
. Dann gilt 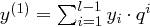 und somit folgt wie in Lemma 8
und somit folgt wie in Lemma 8
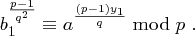
Also wird 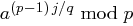 berechnet,
berechnet, 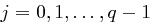 , bis
, bis 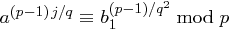 erfüllt ist, dann setzt man
erfüllt ist, dann setzt man 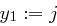 .
.
Das Verfahren wird fortgesetzt. Allgemein wird wie folgt vorgegangen:
Pohlig-Hellman Verfahren:
Gegeben: Ein Tripel 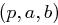 mit
mit 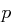 prim,
prim, 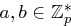 und
und 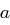 primitiv in
primitiv in 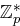 sowie eine Primzahl
sowie eine Primzahl 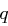 mit
mit 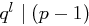 aber
aber 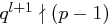 .
.
Gesucht: Ein 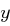 mit
mit 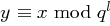 und
und 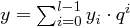 , wobei gilt
, wobei gilt 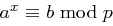 .
.
Man muss maximal 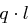 Schritte durchführen, von denen jeder einzelne in Zeit
Schritte durchführen, von denen jeder einzelne in Zeit 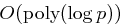 durchführbar ist. Mit
durchführbar ist. Mit 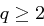 und
und 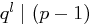 folgt
folgt 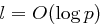 . Gilt für jeden einzelnen Primfaktor
. Gilt für jeden einzelnen Primfaktor  mit
mit 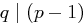 nun
nun 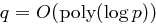 , so löst das Pohlig-Hellman Verfahren das Diskrete Logarithmus Problem in Polynomialzeit, wenn die Primfaktorzerlegung von
, so löst das Pohlig-Hellman Verfahren das Diskrete Logarithmus Problem in Polynomialzeit, wenn die Primfaktorzerlegung von 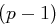 gegeben ist. Letzteres ist natürlich nicht unproblematisch.
gegeben ist. Letzteres ist natürlich nicht unproblematisch.
Zusammenfassend können wir sagen: Ist die Primzahlzerlegung von 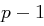 "leicht" zu finden, so ist das Diskrete Logarithmus Problem mit dem Pohlig-Hellman Verfahren "effizient" zu lösen.
"leicht" zu finden, so ist das Diskrete Logarithmus Problem mit dem Pohlig-Hellman Verfahren "effizient" zu lösen.