3. Zusammengesetzte Datentypen

3.2 Erstes Programmierprojekt: Geometrie, Grafik und Modularisierung

Abgabetermin: Sonntag, 3. Dezember 2023.

Aufgaben: Die in diesem Teilkapitel (3.2) als Testataufgabe gekennzeichneten Aufgaben.

Format: Elm-Quelldateien, wie weiter unten beschrieben.

Material: Die Quelldateien des Projekts mit einer fehlerhaften Dummy-Implementierung von mir: project-1-geometry.zip. Wie Sie mit diesen Dateien vorgehen, ist weiter unten genauer beschrieben.

In diesem Projekt werden wir zusammen mehrere Applikationen programmieren. Ein Beispiel sehen Sie hier:

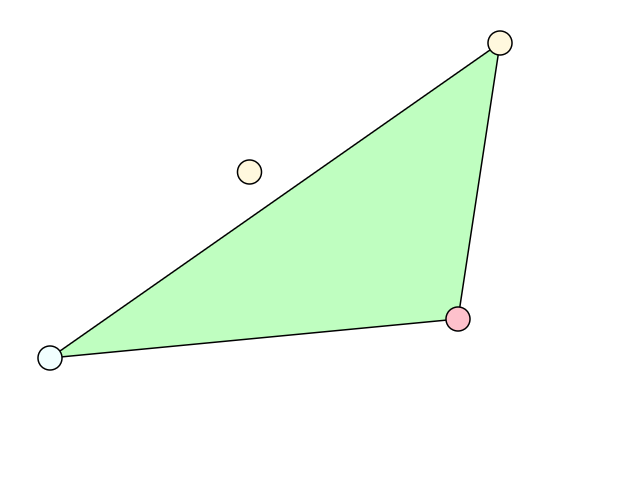
In dieser App können Sie bis zu drei Punkte in das Spielfeld klicken. Sobald Sie drei Punkte haben, wird das Dreieck eingefäbt, und zwar abhängig davon, ob die Maus innerhalb oder außerhalb des Dreiecks ist.

Modularisierung

Eins der wichtigsten Prinzipien beim Programmieren ist die Modularisierung. Das heißt, dass Sie Ihren Code in sinnvolle, wiederverwertbare Einheiten (genannt Module) trennen. Um ein Modul verwenden zu können, muss ich wissen, was es implementiert, nicht wie es implementiert wird. In etwa so, wie Sie beim Kauf einer Glühbirne die Spezifikationen (Spannung, Leistung, Art des Gewindes) wissen müssen, aber eben nichts davon verstehen müssen, wie die Glühbirne funktioniert.

Modularisierung dient der Zusammenarbeit. Sie werden den Großteil Ihres Arbeitslebens nicht alleine programmieren, sondern in Zusammenarbeit mit anderen. Dies tun Sie auch im Rahmen dieses Projekts.

Was ich mache: ich schreibe in diesem Projekt das "Front End", also die grafische Benutzeroberfläche. Im Moment würde das auch Ihre Kenntnisse übersteigen. Mein Code benutzt ein Modul GeometryTypes, welches die Typen Vector, DirectedLine und Triangledefiniert. Diese Modul stelle ich Ihnen bereit. Des Weiteren benutzt es ein Modul GeometryFunctions, welches die folgenden Funktionen implementiert:

leftRightOrOnLine : DirectedLine -> Vector -> Int
insideTriangle : Triangle -> Vector -> Bool
pointOnLineClosestTo : DirectedLine -> Vector -> Vector

Was Sie machen: Sie implementieren das Modul GeometryFunctions, also die verlangten drei Funktionen.

Worüber wir kommunizieren müssen: Stellen Sie sich vor, Sie wären ein Team von Softwareentwicklern und ich wäre ein anderes Team. Unsere Kompetenzen sind verschieden: Ihr Team besteht aus Spezialisten für geometrische Algorithmen; mean Team besteht aus Spezialisten für Webentwicklung, Frontends und grafische Benutzeroberflächen. Es gibt nur wenig Überschneidung unserer Kompetenzen. Daher ist es wichtig, die Schnittstelle kleinzuhalten, also das, worüber wir kommunizieren müssen, was wir beide verstehen müssen. Und die Schnittstelle ist eben genau dies: die Typen, die in GeometryTypes definiert sind, und die Signaturen der Funktionen, die Sie in GeometryFunctions implementieren sollen. Am wichtigsten und schwierigsten aber: was diese Funktionen denn tun sollen, also deren Semantik. Versuchen wir es.

• leftRightOrOnLine line v gibt 1, -1, oder 0 zurück, je nachdem, ob der Punkt v links von, rechts von oder auf der gerichteten Gerade line liegt.
• insideTriangle triangle v gibt True zurück, wenn v im Inneren des Dreiecks liegt, ansonsten False.
• pointOnLineClosestTo line v gibt den Punkt u auf der Gerade line zurück, der am nächsten zu v liegt; also den Fußpunkt, wenn Sie von v aus ein Lot auf line fällen.

Meine Dummy-Implementierung und wie Sie sie starten.

"Mein" Code, also die grafische Oberfläche, ist schon fertig. Damit Sie gleich starten können, habe ich eine Dummy-Implementierung von GeometryFunctions geschrieben. Darin sind die Funktionen zwar alle vorhanden, geben aber inkorrekte Werte zurück. Der Zweck ist, dass Sie einen lauffähigen Code haben, auf dem Sie aufbauen können.

Laden Sie sich nun project-1-geometry.zip herunter, speichern es in Ihrem PP-Order, also unter H:\PP\ und entkomprimieren ihn dann. Gehen Sie auf der Konsole in den dekomprimierten Ordner.

C:\> H:\
H:\> cd PP\project-1-geometry
H:\PP\project-1-geometry\>

Sie können jetzt natürlich Elm im Relp-Modus starten und mit meiner Dummy-Implementierung rumspielen:

H:\PP\project-1-geometry\> elm repl                        
import GeometryTypes exposing (..)
import GeometryFunctions exposing (..)
p = {x = 0, y = 0}
q = {x = 3, y = 1}
line = {from = p, to = q}
v = {x = 1, y = 0}
leftRightOrOnLine line v
1 : Int

Der Code läuft also, ist aber nicht korrekt. Der Punkt \(v\) liegt nämlich rechts von der gerichteten Geraden, die Funktion hätte also -1 ausgeben müssen (zeichnen Sie die drei Punkte in einem Koordinatensystem, um sich zu überzeugen). Wenn Sie Ihren Code testen wollen, so können Sie natürlich jederzeit das Repl-Fenster starten. Achten Sie aber immer auf die beiden import-Befehle.

Eine Elm-App im Browser starten: elm reactor

Um aber nun die grafische Benutzeroberfläche zu sehen, öffnen Sie eine weitere Konsole und gehen in den Ordner. Dann rufen Sie elm reactor auf:

C:\> H:\
H:\> cd PP\project-1-geometry
H:\PP\project-1-geometry\>elm reactor
Go to http://localhost:8000 to see your project dashboard.

Der Befehl elm reactor startet auf Ihrem Rechner einen Webserver. Öffnen Sie nun http://localhost:8000. Sie sehen den Inhalt des Ordners project-1-geometry mit drei Einträgen: geometry, src und elm.json. Klicken Sie auf src und dann auf eine der Drei Dateien, die mit DemoDrop... beginnen. Die Elm-Apps laufen nun in Ihrem Browser. Aber sie tun nicht das, was sie soll. Die App DemoDropTriangle.elm zum Beispiel (Link funktioniert nur, wenn Sie den Elm-Reactor-Server wie oben beschrieben gestartet haben) testet nicht, ob die Maus innerhalb des Dreicks liegt, sondern ob sie links vom ältesten Punkt (dem blassgelben) liegt. Das ist mit v.x \lt triangle.a.x natürlich einfach getestet. Meine Dummy-Implementierung in GeometryFunctions dient auch nur dazu, die App zum Laufen zu bringen.

Ihre Testataufgaben

leftRightOrOnLine : DirectedLine -> Vector -> Int
insideTriangle : Triangle -> Vector -> Bool
pointOnLineClosestTo : DirectedLine -> Vector -> Vector

module GeometryFunctionsVornameNachname exposing (..)

import GeometryFunctionsVornameNachname exposing (..) import GeometryFunctions exposing (..)

testTriangle1 : Bool
testTriangle1 =
    let
        a : Vector
        a =
            { x = 1, y = 0 }

        b : Vector
        b =
            { x = 0, y = 0 }

        c : Vector
        c =
            { x = 0, y = 1 }

        triangle : Triangle
        triangle =
            { a = a, b = b, c = c }

        {--beachten Sie, dass in der Schreibweise "a = a" das erste a der Name 
        der Record-Variable ist; das zweite a ist der Bezeichner, den wir in Zeile 11 
        definiert haben.
        --}
        testPoint : Vector
        testPoint =
            { x = 0.6, y = 0.5 }

        -- dieser Punkt ist nicht im Dreieck drinnen
    in
    -- Test bestanden wenn die Funktion insideTriangle False zurückgibt
    not (insideTriangle triangle testPoint)

Nachtrag zur obigen Testataufgabe: Ihre Test-Cases sollten allesamt den Wert Bool annehmen. Um zum Beispiel pointOnLineClosestTo zu testen, machen Sie es :

testPointClosest1 : Bool 
testPointClosest1 = 
    let 
        a = {x = 0, y = 0}
        b = {x = 2, y = 2}

        c = {x = 2, y = 0}

        line : {from = a, to = b}

        trueAnswer = {x = 1, y = 1} -- was Sie als korrekte Antwort ausgerechnet haben
    in 
    pointOnLineClosestTo line c == trueAnswer