Visualisierung mit Matplotlib
Contents
4. Visualisierung mit Matplotlib¶
Matplotlib ist eine mächtige Python-Bibliothek, welche viele Funktionen für die graphische Darstellung in Form von Plots und Diagrammen bereitstellt. Wir werden in diesem Abschnitt die grundlegende Funktionsweise kennenlernen.
4.1. Erste Schritte¶
Ähnlich wie bei NumPy müssen wir Matplotlib erst installieren. Man kann entweder direkt das Paket python3-matplotlib über den Paketmanager der Linux-Distribution installieren, das Verwaltungsprogramm pip nutzen, oder über die Conda-Distribution gehen:
conda install -c conda-forge matplotlib
Anschließend können wir Matplotlib, besser gesagt das Submodul matplotlib.pyplot in unser Programm einbinden:
import matplotlib.pyplot as plt
Der wichtigste Befehl ist plt.plot(...). Wir geben plt.plot? ein um zu erfahren wie dieser funktioniert. In der einfachsten Form sind die Argumente dieser Funktion 2 Vektoren mit \(x\)- bzw. \(y\)-Koordinaten einer Punktwolke. Diese Vektoren können Listen, oder Numpy-Arrays sein. Die Sinusfunktion können wir wie folgt plotten:
import numpy as np
x = np.linspace(0,2*np.pi, 11) # Erzeuge Gitter [0, 0.2*pi, 0.4*pi, ..., 2*pi])
y = np.sin(x) # Berechne zugehörige Funktionswerte
plt.plot(x,y) # Erzeuge Plot
plt.show() # Zeige den Plot
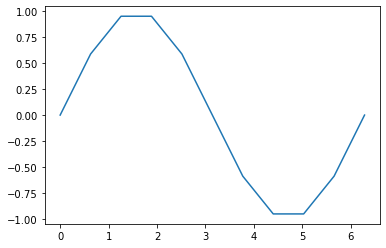
Hier sehen wir auch eine schöne Anwendung der komponentenweise definierten mathematischen Funktionen aus numpy.
Übungsaufgabe
Plotte die Funktion \(f(x) = e^{-x}\,\sin(2\,\pi\,x)\) im Intervall \([0,6]\).
4.2. Gestaltung von Plots¶
Machen wir unseren Plot noch etwas schöner:
import numpy as np
x = np.linspace(0,4*np.pi, 1001) # Erzeuge Gitter [0, 0.2*pi, 0.4*pi, ..., 2*pi])
y = np.sin(x) # Berechne zugehörige Funktionswerte für sinus
z = np.cos(x) # und cosinus
plt.figure(figsize=(10,5)) # Größe einstellen
plt.plot(x,y,label="$\sin(x)$") # Erzeuge Plot für Sinus
plt.plot(x,z,label="$\cos(x)$") # Erzeuge Plot für Cosinus
plt.title("Sinus und Cosinus") # Titel des Plots
plt.grid() # Gitterlinien einschalten
plt.xlabel('x') # Bezeichner an x-Achse
plt.ylabel('f(x)') # Bezeichner an y-Achse (in Latex-Code)
plt.legend() # Legende
plt.show() # Zeige den Plot
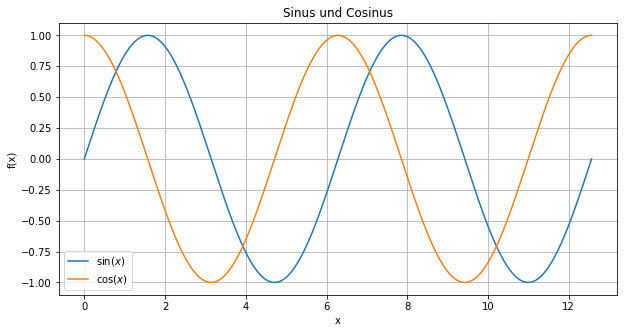
Im Prinzip hat Matplotlib unsere Punktwolke mit Koordinaten aus x und y gezeichnet, und die Punkte mit Linen verbunden. Es gibt aber noch einige andere Linientypen:
x = np.linspace(0,2,21)
y1= x**2-x
y2= 2*x-x**2
y3= 3*x-1.5*x**2
plt.figure(figsize=(10,5)) # Größe einstellen
# Zeichne rote (r) Kreise (o) mit Verbindungslinien (-)
plt.plot(x, y1, 'ro-', linewidth=0.2)
# Zeichne blaue (b) Quadrate (s)
plt.plot(x, y2, 'bs')
# Zeichne cyane (c) Dreiecke (^) mit gestrichelten Verbindungslinien (--)
plt.plot(x, y3, 'c^--', markersize=10)
plt.show()
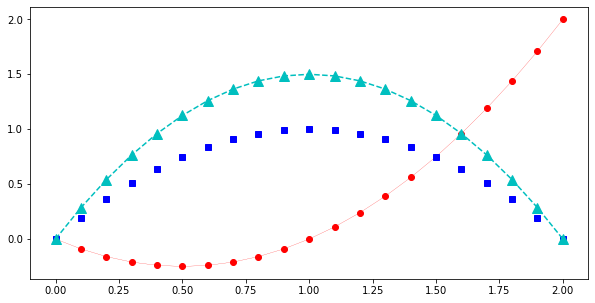
Im Hilfetext plt.plot? sind noch weitere Linien- und Markertypen erklärt. Vordefinierte Farben im Submodul matplotlib.colors. Es gibt verschiedene Farbpaletten. Die Grundfarben sind:
import matplotlib.colors as mcolors
mcolors.BASE_COLORS
{'b': (0, 0, 1),
'g': (0, 0.5, 0),
'r': (1, 0, 0),
'c': (0, 0.75, 0.75),
'm': (0.75, 0, 0.75),
'y': (0.75, 0.75, 0),
'k': (0, 0, 0),
'w': (1, 1, 1)}
Es gibt weiterhin die Farbpalette Tableau:
mcolors.TABLEAU_COLORS
{'tab:blue': '#1f77b4',
'tab:orange': '#ff7f0e',
'tab:green': '#2ca02c',
'tab:red': '#d62728',
'tab:purple': '#9467bd',
'tab:brown': '#8c564b',
'tab:pink': '#e377c2',
'tab:gray': '#7f7f7f',
'tab:olive': '#bcbd22',
'tab:cyan': '#17becf'}
Und außerdem noch CSS-Farben:
mcolors.CSS4_COLORS
{'aliceblue': '#F0F8FF',
'antiquewhite': '#FAEBD7',
'aqua': '#00FFFF',
'aquamarine': '#7FFFD4',
'azure': '#F0FFFF',
'beige': '#F5F5DC',
'bisque': '#FFE4C4',
'black': '#000000',
'blanchedalmond': '#FFEBCD',
'blue': '#0000FF',
'blueviolet': '#8A2BE2',
'brown': '#A52A2A',
'burlywood': '#DEB887',
'cadetblue': '#5F9EA0',
'chartreuse': '#7FFF00',
'chocolate': '#D2691E',
'coral': '#FF7F50',
'cornflowerblue': '#6495ED',
'cornsilk': '#FFF8DC',
'crimson': '#DC143C',
'cyan': '#00FFFF',
'darkblue': '#00008B',
'darkcyan': '#008B8B',
'darkgoldenrod': '#B8860B',
'darkgray': '#A9A9A9',
'darkgreen': '#006400',
'darkgrey': '#A9A9A9',
'darkkhaki': '#BDB76B',
'darkmagenta': '#8B008B',
'darkolivegreen': '#556B2F',
'darkorange': '#FF8C00',
'darkorchid': '#9932CC',
'darkred': '#8B0000',
'darksalmon': '#E9967A',
'darkseagreen': '#8FBC8F',
'darkslateblue': '#483D8B',
'darkslategray': '#2F4F4F',
'darkslategrey': '#2F4F4F',
'darkturquoise': '#00CED1',
'darkviolet': '#9400D3',
'deeppink': '#FF1493',
'deepskyblue': '#00BFFF',
'dimgray': '#696969',
'dimgrey': '#696969',
'dodgerblue': '#1E90FF',
'firebrick': '#B22222',
'floralwhite': '#FFFAF0',
'forestgreen': '#228B22',
'fuchsia': '#FF00FF',
'gainsboro': '#DCDCDC',
'ghostwhite': '#F8F8FF',
'gold': '#FFD700',
'goldenrod': '#DAA520',
'gray': '#808080',
'green': '#008000',
'greenyellow': '#ADFF2F',
'grey': '#808080',
'honeydew': '#F0FFF0',
'hotpink': '#FF69B4',
'indianred': '#CD5C5C',
'indigo': '#4B0082',
'ivory': '#FFFFF0',
'khaki': '#F0E68C',
'lavender': '#E6E6FA',
'lavenderblush': '#FFF0F5',
'lawngreen': '#7CFC00',
'lemonchiffon': '#FFFACD',
'lightblue': '#ADD8E6',
'lightcoral': '#F08080',
'lightcyan': '#E0FFFF',
'lightgoldenrodyellow': '#FAFAD2',
'lightgray': '#D3D3D3',
'lightgreen': '#90EE90',
'lightgrey': '#D3D3D3',
'lightpink': '#FFB6C1',
'lightsalmon': '#FFA07A',
'lightseagreen': '#20B2AA',
'lightskyblue': '#87CEFA',
'lightslategray': '#778899',
'lightslategrey': '#778899',
'lightsteelblue': '#B0C4DE',
'lightyellow': '#FFFFE0',
'lime': '#00FF00',
'limegreen': '#32CD32',
'linen': '#FAF0E6',
'magenta': '#FF00FF',
'maroon': '#800000',
'mediumaquamarine': '#66CDAA',
'mediumblue': '#0000CD',
'mediumorchid': '#BA55D3',
'mediumpurple': '#9370DB',
'mediumseagreen': '#3CB371',
'mediumslateblue': '#7B68EE',
'mediumspringgreen': '#00FA9A',
'mediumturquoise': '#48D1CC',
'mediumvioletred': '#C71585',
'midnightblue': '#191970',
'mintcream': '#F5FFFA',
'mistyrose': '#FFE4E1',
'moccasin': '#FFE4B5',
'navajowhite': '#FFDEAD',
'navy': '#000080',
'oldlace': '#FDF5E6',
'olive': '#808000',
'olivedrab': '#6B8E23',
'orange': '#FFA500',
'orangered': '#FF4500',
'orchid': '#DA70D6',
'palegoldenrod': '#EEE8AA',
'palegreen': '#98FB98',
'paleturquoise': '#AFEEEE',
'palevioletred': '#DB7093',
'papayawhip': '#FFEFD5',
'peachpuff': '#FFDAB9',
'peru': '#CD853F',
'pink': '#FFC0CB',
'plum': '#DDA0DD',
'powderblue': '#B0E0E6',
'purple': '#800080',
'rebeccapurple': '#663399',
'red': '#FF0000',
'rosybrown': '#BC8F8F',
'royalblue': '#4169E1',
'saddlebrown': '#8B4513',
'salmon': '#FA8072',
'sandybrown': '#F4A460',
'seagreen': '#2E8B57',
'seashell': '#FFF5EE',
'sienna': '#A0522D',
'silver': '#C0C0C0',
'skyblue': '#87CEEB',
'slateblue': '#6A5ACD',
'slategray': '#708090',
'slategrey': '#708090',
'snow': '#FFFAFA',
'springgreen': '#00FF7F',
'steelblue': '#4682B4',
'tan': '#D2B48C',
'teal': '#008080',
'thistle': '#D8BFD8',
'tomato': '#FF6347',
'turquoise': '#40E0D0',
'violet': '#EE82EE',
'wheat': '#F5DEB3',
'white': '#FFFFFF',
'whitesmoke': '#F5F5F5',
'yellow': '#FFFF00',
'yellowgreen': '#9ACD32'}
Durch Setzen des Parameters color im Plot-Befehl kann nun eine Farbe aus einer der oberen Farbpaletten gewählt werden:
x = np.linspace(0,1,10)
plt.plot(x,0.5*x*(1-x),'o-',color='g') # Grundfarbe
plt.plot(x,x*(1-x),'d-',color='tab:olive') # Tableau-Farbe
plt.plot(x,1.5*x*(1-x),'s-',color='firebrick') # CSS-Farbe
plt.show()
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_colortable(colors, title, sort_colors=True, emptycols=0):
cell_width = 212
cell_height = 22
swatch_width = 48
margin = 12
topmargin = 40
# Sort colors by hue, saturation, value and name.
if sort_colors is True:
by_hsv = sorted((tuple(mcolors.rgb_to_hsv(mcolors.to_rgb(color))),
name)
for name, color in colors.items())
names = [name for hsv, name in by_hsv]
else:
names = list(colors)
n = len(names)
ncols = 4 - emptycols
nrows = n // ncols + int(n % ncols > 0)
width = cell_width * 4 + 2 * margin
height = cell_height * nrows + margin + topmargin
dpi = 72
fig, ax = plt.subplots(figsize=(width / dpi, height / dpi), dpi=dpi)
fig.subplots_adjust(margin/width, margin/height,
(width-margin)/width, (height-topmargin)/height)
ax.set_xlim(0, cell_width * 4)
ax.set_ylim(cell_height * (nrows-0.5), -cell_height/2.)
ax.yaxis.set_visible(False)
ax.xaxis.set_visible(False)
ax.set_axis_off()
ax.set_title(title, fontsize=24, loc="left", pad=10)
for i, name in enumerate(names):
row = i % nrows
col = i // nrows
y = row * cell_height
swatch_start_x = cell_width * col
text_pos_x = cell_width * col + swatch_width + 7
ax.text(text_pos_x, y, name, fontsize=14,
horizontalalignment='left',
verticalalignment='center')
ax.add_patch(
Rectangle(xy=(swatch_start_x, y-9), width=swatch_width,
height=18, facecolor=colors[name], edgecolor='0.7')
)
return fig
plot_colortable(mcolors.BASE_COLORS, "Grundfarben",
sort_colors=False, emptycols=1)
plot_colortable(mcolors.TABLEAU_COLORS, "Tableau-Palette",
sort_colors=False, emptycols=2)
plot_colortable(mcolors.CSS4_COLORS, "CSS-Farben")
# Optionally plot the XKCD colors (Caution: will produce large figure)
# xkcd_fig = plot_colortable(mcolors.XKCD_COLORS, "XKCD Colors")
# xkcd_fig.savefig("XKCD_Colors.png")
plt.show()
Bei der Fehleranalyse sind oft logarithmische Achsen von interesse. Angenommen, wir analysieren einen iterativen Algorithmus und messen die Entfernung \(\text{err}_n\) zwischen exakter Lösung und der berechnete Näherungslösung nach \(n\) Iterationen. Man sagt, das Verfahren konvergiert
Q-linear, falls \(\text{err}_n \le C\, \text{err}_{n-1}\) mit \(C\in (0,1)\)
Q-superlinear, falls \(\text{err}_n \le \varepsilon_n\,\text{err}_{n-1}\) mit einer Nullfolge \(\varepsilon_n\searrow 0\)
Q-quadratisch, falls \(\text{err}_n \le C\, \text{err}_{n-1}^2\) mit \(C>0\).
Stellen wir den Fehlerverlauf in einem kartesischen Koordinatensystem und einem Koordinatensystem mit logarithmischer \(y\)-Achse dar:
import math
n = np.array(range(1,6), dtype='float64')
err_p1 = (0.8)**n
err_p2 = [1./math.factorial(int(i)) for i in n]
err_p3 = (0.8)**(2**n)
plt.figure(figsize=(10,5))
def generate_plot():
plt.plot(n, err_p1, 'ro-', label='Q-linear')
plt.plot(n, err_p2, 'bo-', label='Q-superlinear')
plt.plot(n, err_p3, 'co-', label='Q-quadratisch')
plt.grid()
# Plot in kartesischen Koordinatensystem
plt.subplot(1,2,1)
generate_plot()
plt.legend(loc='upper right')
# Plot in Koordinatensystem mit logarithmischer y-Achse
plt.subplot(1,2,2)
generate_plot()
plt.semilogy()
plt.legend(loc='lower left')
plt.show()
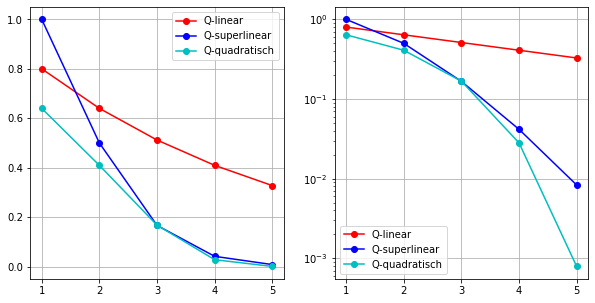
Wir sehen, dass eine \(Q\)-linear konvergente Folge im Plot mit logarithmischer \(y\)-Achse einer lineare Funktion ist.
Analog dazu kann man auch die \(x\)-Achse mit plt.semilogx() logatithmisch skalieren, was bei oben vorgestellter Anwendung allerdings wenig Sinn macht.
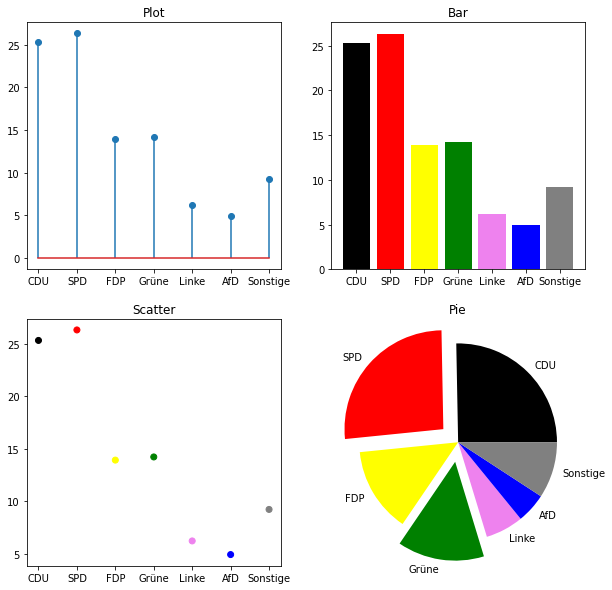
Schauen wir uns weitere elementare Plot-Typen an. Angenommen wir haben die Auswertung einer Umfrage vorliegen, und möchten diese graphisch aufbereiten. Unsere Beispieldaten sind:
parties = ["CDU", "SPD", "FDP", "Grüne", "Linke", "AfD", "Sonstige"]
colors = ["black", "red", "yellow", "green", "violet", "blue", "gray"]
values = [25.3, 26.3, 13.9, 14.2, 6.2, 4.9]
values.append(100-sum(values))
Wir können anstelle des plot-Befehls auch stem verwenden um ein Liniendiagramm zu erstellen, scatter für ein Streudiagramm, bar für ein Balkendiagramm oder pie für ein Tortendiagramm. Im folgenden Beispiel werden die Unterschiede gezeigt:
plt.figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.stem(parties, values)
plt.title("Plot")
plt.subplot(2,2,2)
plt.bar(parties, values, color=colors)
plt.title("Bar")
plt.subplot(2,2,3)
plt.scatter(parties, values, color=colors)
plt.title("Scatter")
plt.subplot(2,2,4)
plt.pie(values, labels=parties, explode=[0,0.2,0,0.2,0,0,0], colors=colors)
plt.title("Pie")
plt.show()
4.3. Plots für Skalar- und Vektorfelder¶
Auch für die graphische Darstellung von Skalarfeldern \(f\colon \mathbb{R}^2 \to \mathbb{R}\) und Vektorfeldern \(\vec F\colon \mathbb{R}^2 \to \mathbb{R}^2\) stehen einige Funktionen in Matplotlib bereit. Die meisten Funktionen zur Darstellung von Skalarfeldern erwarten als Argument 3 Matrizen, eine für die \(x\)-Koordinaten, eine für die \(y\)-Koordinaten und eine für den Funktionswert \(f(x,y)\). Hilfreich ist hier die Funktion numpy.meshgrid mit der wir ein 2D-Tensorprodukt-Gitter aus 2 1D-Gittern erzeugen:
# 1D-Gitter für x- und y-Variable
x = np.linspace(-4.5,3.5,1001)
y = np.linspace(-3.5,3.5,1001)
# 2D-Gitter erzeugen
X,Y = np.meshgrid(x,y)
# Definiere Himmelblau-Funktion
Z = (X**2 + y - 11)**2 + (X + Y**2 - 7)**2
Eine mögliche Darstellung einer solchen Funktion wäre ein Contour-Plot, in welchem die Kurven \(\{(x,y)\colon f(x,y)=c_i\}\) für verschiedene Werte \(c_1<c_2 < \ldots<c_{\text{levels}}\) eingezeichnet werden:
plt.contour(X,Y,Z, levels=25)
plt.colorbar()
plt.show()
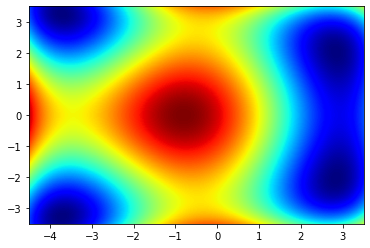
Ähnlich funktionieren Color-Plots, bei denen der Funktionswert an einer Stelle \((x,y)\) dem Farbwert einer vordefinierten Farbpalette entspricht:
import matplotlib.cm as cm
plt.pcolormesh(X,Y,Z, cmap=cm.jet)
plt.show()
Skalarfelder lassen sich auch in dreidimensionalen Koordinatensystemen darstellen. Die Argumente werden auf \(x\)- und \(y\)-Achse aufgetragen, und der Funktionswert auf die \(z\)-Achse. Die entsprechenden Plot-Befehle sind allerdings nicht im Submodul matplotlib.pyplot definiert, daher müssen wir einen Umweg nehmen. Zunächst erzeugen wir uns ein Bildobjekt mit
fig = plt.figure()
fügen ein 3D-Koordinatensystem hinzu
ax = fig.axes(projection='3d')
und nutzen die vom Objekt ax bereitgestellten Plot-Befehle. Hier ein Beispiel:
plt.figure(figsize=(8,6))
# 3D-Koordinatensystem hinzufügen
ax = plt.axes(projection='3d')
# Surface-Plot erstellen
ax.plot_surface(X,Y,Z, cmap=cm.inferno)
plt.show()
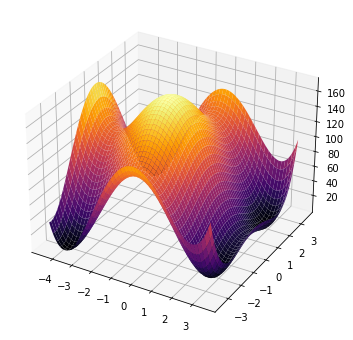
plt.figure(figsize=(8,6))
ax = plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z, rcount=10)
plt.show()
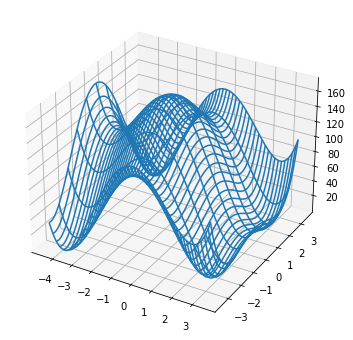
Schauen wir uns noch eine Methode mit der wir Vektorfelder zeichnen können. Als Beispiel definieren wir \(\vec f(x,y) = (-y,x)^\top\). Solche Vektorfelder können in sogenannten Quiver-Plots dargestellt werden:
x = np.linspace(-1,1, 11)
y = np.linspace(-1,1, 11)
# Punktgitter definieren
X,Y = np.meshgrid(x, y)
# Funktionswerte von F
Z1 = -Y
Z2 = X
# Optional: Färbe Pfeile nach Länge
C = np.sqrt(Z1**2 + Z2**2)
# Quiverplot erzeugen und anzeigen
plt.quiver(X, Y, Z1, Z2, C, cmap=cm.rainbow)
plt.show()
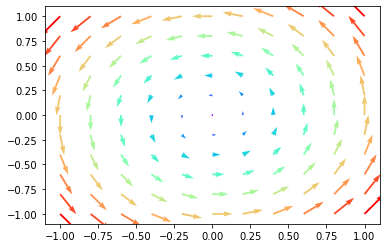
Auch Kurven lassen sich in Matplotlib zeichnen. Eine Kurve ist zunächst eine Menge an Punkten
mit einer sogenannten Kurvenparametrisierung \(\vec x\colon[t_a,t_b]\to\mathbb{R}^n\), welche regulär ist, d.h., \(\dot{\vec x}(t)\ne 0\) für alle \(t\in [t_a,t_b]\). Für eine ebene Kurve (\(n=2\)) können wir den normalen Plot-Befehl nutzen. Das Kleeblatt
zeichnen wir beispielsweise mit
t = np.linspace(0,2*np.pi,100)
x = np.cos(t)+np.cos(2*t)
y = np.sin(t)-np.sin(2*t)
plt.plot(x,y,'o-')
plt.grid()
plt.show()
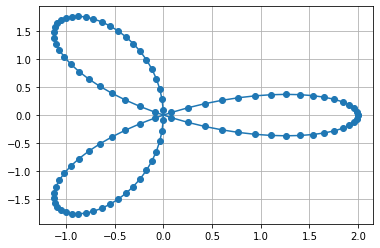
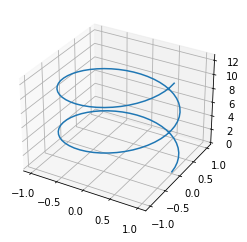
Ähnlich kann man Raumkurven (\(n=3\)) zeichnen, man benötigt nur vorher ein dreidimensionales Koordinatensystem. Wie wir das anlegen haben wir aber schon gesehen. Wir zeichnen hier die Schraubenlinie
t = np.linspace(0,4*np.pi,100)
x = np.cos(t)
y = np.sin(t)
z = t
ax = plt.axes(projection='3d')
ax.plot3D(x, y, z)
plt.show()
