Leistungssatz
Die Momente / Kräfte in einem Getriebe oder an einem Glied stehen im Gleichgewicht, wenn die Summe ihrer Leistungen = 0 ist.
\[ \sum_{i} P_{i} = \sum_{i} \vec{M_i} \cdot \vec{\omega_i} + \sum_{i} \vec{F_i} \cdot \vec{v_i} + P_V = 0\]zeichnerische Methoden
Methode der h-Strecke
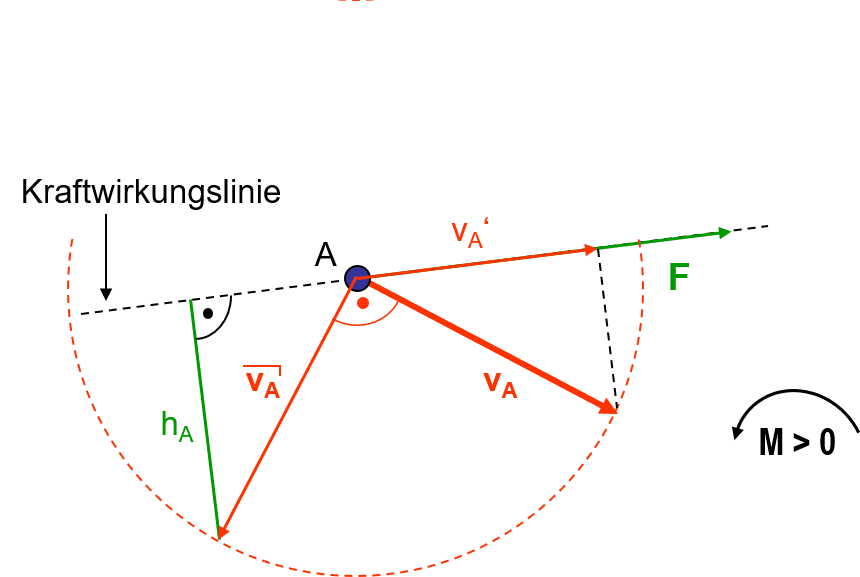
Die Methode der h-Strecke kann sowohl für die Ermittlung der in einem Getriebe wirkenden Kräfte als auch für die Ermittlung der auftretenden Geschwindigkeiten eingesetzt werden. Die h-Strecke ist:
- die des Geschwindigkeitsanteils des Kraftangriffspunktes in der Kraftwirkungslinie
- der senkrechte Abstand der Kraftwirkungslinie zur Spitze der gedrehten Geschwindigkeit
- maßstabsbehaftet (\(M_V\))
Vorgehen:
- Aufstellen der Ansatzgleichung: \( \sum_{i} F_{i} \cdot h_{i} = 0\)
(Das Vorzeichen der Kraft in der Ansatzgleichung ergibt sich aus der Drehrichtung der Kraft um die Spitze der gedrehten Geschwindigkeit)
- Umstellen der Gleichung nach der gesuchten Größe
- Ermittlung der benötigten h-Strecken
- Einsetzen der h-Strecken in die Gleichung
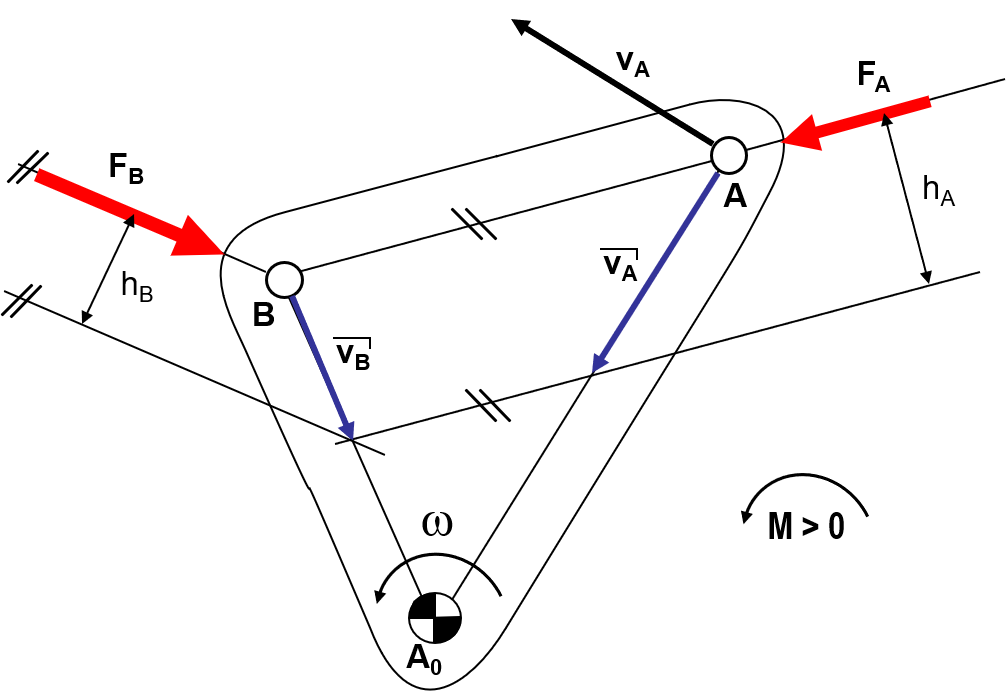
Beispiel
geg.:
- Kraft \(F_A\)
- Wirkungslinie der Kraft \(F_B\)
- beliebige Geschwindigkeit \(v_A\)
ges.:
- Kraft \(F_B\)
Lösung:
- \(\sum F_i \cdot h_i=0\)
- \(F_A \cdot h_A-F_B \cdot h_B=0\)
- \(F_B=F_A \cdot h_A/h_B\)
Beispielaufgabe "Hängeschranktür"
Ermittlung des Antriebsmomentes aus dem Arbeitswiderstand
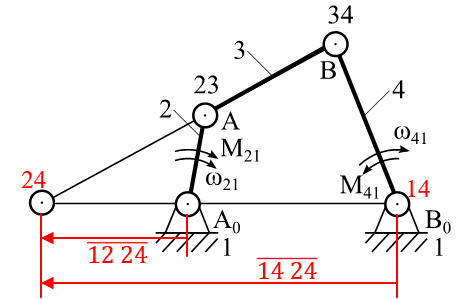
Leistungssatz mit Übersetzung
geg.:
- Kraft \(F_A\)
- Wirkungslinie der Kraft \(F_B\)
- beliebige Geschwindigkeit \(v_A\)
ges.:
- Kraft \(F_B\)
Lösung:
- \(\sum F_i \cdot h_i=0\)
- \(F_A \cdot h_A-F_B \cdot h_B=0\)
- \(F_B=F_A \cdot h_A/h_B\)
Stehen an einem Getriebe zwei Momente im Gleichgewicht (z. B. am An- und Abtriebsglied) so kann ihr Verhältnis,
unter Vernachlässigung der Verlust- und Trägheitskräfte, durch die Übersetzung dargestellt werden.
\(\rightarrow \) zwei drehende Bezugsglieder
Vorgehen:
- Ansatzgleichung aufstellen: \( \sum_{i} M_{i} \cdot \omega_{i} = 0\)
- Umstellen der Gleichung nach der gesuchten Größe
- Ermittlung der benötigten Momentanpole
- Ermittlung der benötigten Momentanpol-Strecken rij
- Einsetzen der ermittelten Strecken
Beispiel
geg.:
- Moment \( M_{41}\)
- Winkelgeschwindigkeit \(\omega_{21} \)
ges.:
- Moment \(M_{21}\)
Lösung:
- \(M_{21} \cdot \omega_{21} + M_{41} \cdot \omega_{41} = 0 \)
- \(M_{21} =-\frac{\omega_{41}}{\omega_{21}} \cdot M_{41} = -i_{41-21} \cdot M_{41} = - \frac{\overline{12 24}}{\overline{14 24}} \cdot M_{41}\)
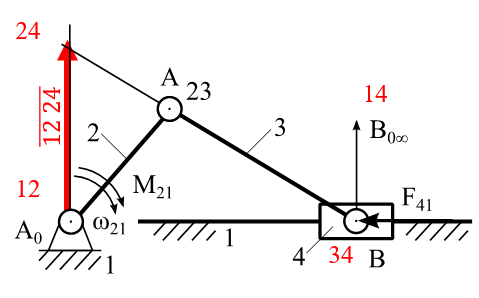
Methode der Drehschubstrecke
Stehen an einem Getriebe ein Moment und eine Kraft im Gleichgewicht (z. B. Antriebsmoment und Abtriebskraft) so ist ihr Verhältnis,
unter Vernachlässigung der Verlust- und Trägheitskräfte, durch die Drehschubstrecke definiert.
\(\rightarrow\) drehendes und schiebendes Bezugsglied
Vorgehen:
- Aufstellen der Ansatzgleichung: \( \sum_{i} M_{i} \cdot \omega_{i} + \sum_{i} F_{i} \cdot v_{i} = 0\)
- Umstellen der Gleichung nach der gesuchten Größe
- Ermittlung der benötigten Momentanpole
- Drehschubstrecke bestimmen und in die Gleichung einsetzen
Beispiel
geg.:
- Kraft \( F_{41}\)
- Winkelgeschwindigkeit \(\omega_{21} \)
ges.:
- Moment \(M_{21}\)
Lösung:
- \(M_{21} \cdot \omega_{21} + F_{41} \cdot v_{41} = 0 \)
- \(M_{21} =-\frac{v_{41}}{\omega_{21}} \cdot F_{41} = -r_{41-21} \cdot F_{41} = - \overline{12 24} \cdot M_{41}\)
- \(r_{41-21} =\frac{v_{41}}{\omega_{21}} = - \frac{M_{21}}{F_{41}} = \overline{12 24}\)
