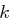 Zeichen, wobei
Zeichen, wobei 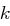 der verwendete Schlüssel ist.
der verwendete Schlüssel ist.
| Allgemeine Methoden | Vigenère-Chiffre |
Verschlüsselung Entschlüsselung Beispiel Kryptoanalyse mit Sprachstatistik Eine zweite Kryptoanalyse Übungen
Die Cäsar-Chiffre ist eines der einfachsten, aber auch unsichersten Verfahren, um Texte zu verschlüsseln. Das Verfahren wurde nach dem römischen Kaiser Julius Cäsar benannt, der auf diese Weise bereits vor über 2000 Jahren Nachrichten verschlüsselt haben soll.
Die Cäsar-Chiffre ist eine monoalphabetische Substitution, das heißt, jeder Buchstabe des Textes wird durch genau einen anderen Buchstaben des Alphabets ersetzt. Dieser Austausch geschieht jedoch nicht zufällig, sondern basiert auf zyklischer Rotation des Alphabets um 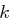 Zeichen, wobei
Zeichen, wobei 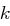 der verwendete Schlüssel ist.
der verwendete Schlüssel ist.
Die Verschlüsselung einer Nachricht erfolgt buchstabenweise mit einem Schlüssel 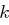 aus der Menge
aus der Menge 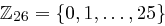 , wobei der Wert
, wobei der Wert 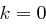 nicht sinnvoll ist, da der Originaltext in diesem Fall keine Änderung erfährt.
nicht sinnvoll ist, da der Originaltext in diesem Fall keine Änderung erfährt.
Für einen gegebenen Buchstaben wird zunächst anhand der folgenden Tabelle seine Position 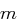 im Alphabet bestimmt.
im Alphabet bestimmt.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
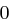 |
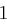 |
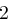 |
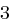 |
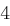 |
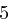 |
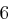 |
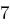 |
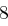 |
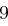 |
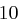 |
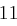 |
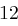 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
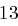 |
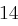 |
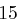 |
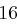 |
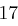 |
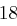 |
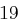 |
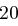 |
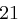 |
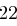 |
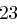 |
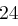 |
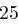 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Anschließend erhält man den Wert 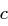 des verschlüsselten Buchstaben durch folgende kurze Berechnungsformel:
des verschlüsselten Buchstaben durch folgende kurze Berechnungsformel:
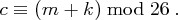
Mit Hilfe obiger Tabelle kann dieser Wert 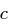 wieder in einen Buchstaben transformiert werden.
wieder in einen Buchstaben transformiert werden.
Die Entschlüsselung einer Nachricht erfolgt ähnlich wie die Verschlüsselung mit Schlüssel 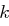 , wir verwenden jedoch die Formel
, wir verwenden jedoch die Formel
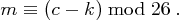
Der Satz "OTTO KOMMT" wird mit dem Schlüssel 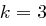 verschlüsselt.
verschlüsselt.
|
|
|
|
|
|
|
|
|
|
|
|
| unverschlüsselt | O | T | T | O | K | O | M | M | T | |
|
|
|
|
|
|
|
|
|
|
|
|
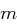 |
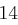 |
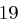 |
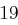 |
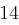 |
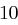 |
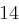 |
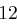 |
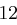 |
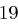 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
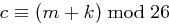 |
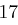 |
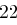 |
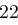 |
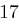 |
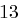 |
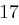 |
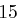 |
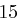 |
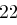 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| verschlüsselt | R | W | W | R | N | R | P | P | W | |
|
|
|
|
|
|
|
|
|
|
|
|
Statt nur über dem Alphabet 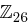 kann man analog allgemeine Cäsar-Chiffre über beliebigen endlichen Alphabeten
kann man analog allgemeine Cäsar-Chiffre über beliebigen endlichen Alphabeten 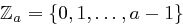 definieren.
definieren.
In diesem Abschnitt wollen wir beispielhaft anhand der Cäsar-Chiffre vorführen, wie die Methode der Sprachstatistik angewendet werden kann. Dazu sei eine allgemeine Cäsar-Chiffre über dem Alphabet 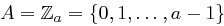 gegeben.
gegeben.
Wir nehmen an, dass die Buchstaben des Klartextes unabhängig voneinander gemäß der Wahrscheinlichkeitsverteilung 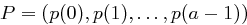 gewählt werden. Der Wert
gewählt werden. Der Wert 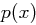 gibt also die Wahrscheinlichkeit für das Auftreten des Buchstabens
gibt also die Wahrscheinlichkeit für das Auftreten des Buchstabens 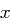 an. Die Annahme über die Verteilung der Buchstaben kann man als in der Realität annähernd erfüllt ansehen.
an. Die Annahme über die Verteilung der Buchstaben kann man als in der Realität annähernd erfüllt ansehen.
Wenn 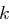 der Schlüssel ist, dann hat das Kryptogramm die Wahrscheinlichkeitsverteilung
der Schlüssel ist, dann hat das Kryptogramm die Wahrscheinlichkeitsverteilung 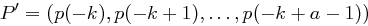 , wobei die Indizes modulo
, wobei die Indizes modulo 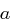 gerechnet werden. Der Vektor der Wahrscheinlichkeitsverteilung
gerechnet werden. Der Vektor der Wahrscheinlichkeitsverteilung 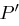 ist also eine zyklische Rotation des Vektors der Verteilung
ist also eine zyklische Rotation des Vektors der Verteilung 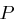 . Wenn man die Größe der Verschiebung bestimmen kann, so hat man den Schlüssel gefunden. Die Größe der Verschiebung bestimmt man nun dadurch, dass man die Positionen beispielsweise der beiden häufigsten, also wahrscheinlichsten Buchstaben im verschobenen Vektor bestimmt und diese mit ihren nicht verschobenen Positionen vergleicht. Dazu überlegen wir uns folgendes.
. Wenn man die Größe der Verschiebung bestimmen kann, so hat man den Schlüssel gefunden. Die Größe der Verschiebung bestimmt man nun dadurch, dass man die Positionen beispielsweise der beiden häufigsten, also wahrscheinlichsten Buchstaben im verschobenen Vektor bestimmt und diese mit ihren nicht verschobenen Positionen vergleicht. Dazu überlegen wir uns folgendes.
Es sei 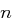 die Länge eines Klartextes und
die Länge eines Klartextes und 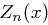 die Zufallsvariable die angibt, wie oft der Buchstabe
die Zufallsvariable die angibt, wie oft der Buchstabe 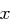 im Klartext vorkommt. Es ergibt sich als Wahrscheinlichkeit, dass der Buchstabe
im Klartext vorkommt. Es ergibt sich als Wahrscheinlichkeit, dass der Buchstabe 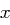 genau
genau 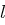 mal im Klartext der Länge
mal im Klartext der Länge 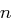 vorkommt
vorkommt
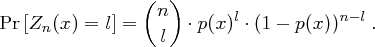
denn man hat 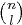 Möglichkeiten,
Möglichkeiten, 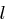 der
der 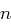 Positionen im Klartext auszuwählen und an diesen
Positionen im Klartext auszuwählen und an diesen 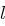 Positionen tritt jeweils mit Wahrscheinlichkeit
Positionen tritt jeweils mit Wahrscheinlichkeit 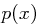 der Buchstabe
der Buchstabe 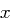 auf und jede andere der
auf und jede andere der 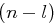 vielen restlichen Positionen enthält kein
vielen restlichen Positionen enthält kein 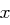 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit 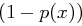 . Somit ergibt sich der Erwartungswert der Zufallsvariable
. Somit ergibt sich der Erwartungswert der Zufallsvariable 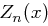 als
als
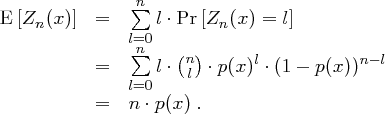
Als Varianz ergibt sich dann
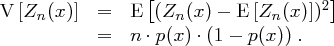
Wir führen eine neue Zuvallsvariable 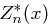 ein mit
ein mit 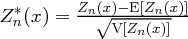 . Die Zufallsvariable
. Die Zufallsvariable 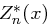 hat eine zentrierte und normierte Binomialverteilung, die sich für große
hat eine zentrierte und normierte Binomialverteilung, die sich für große 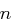 wie eine Standardnormalverteilung verhält. Insbesondere gilt für große
wie eine Standardnormalverteilung verhält. Insbesondere gilt für große 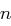
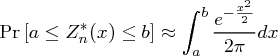
und damit
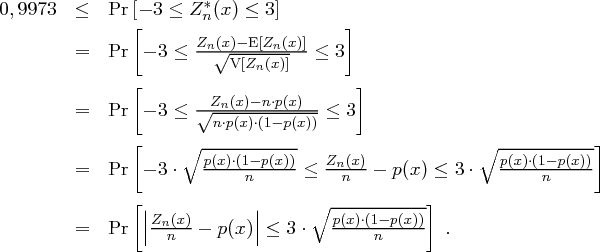
Mit 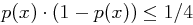 (da im Allgemeinen
(da im Allgemeinen 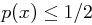 ist) folgt
ist) folgt
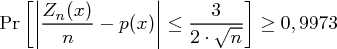
also
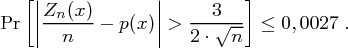
Für die Länge der Nachricht 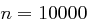 erhält man etwa
erhält man etwa
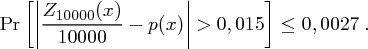
Also ist die Wahrscheinlichkeit, dass die relative Häufigkeit 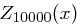 des Buchstaben
des Buchstaben 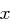 um mehr als 0,015 von der Wahrscheinlichkeit
um mehr als 0,015 von der Wahrscheinlichkeit 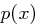 des Auftretens von
des Auftretens von 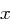 abweicht, kleiner als
abweicht, kleiner als 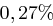 . Betrachtet man das englische Alphabet, so sind die Wahrscheinlichkeiten der beiden häufigsten Buchstaben e und t:
. Betrachtet man das englische Alphabet, so sind die Wahrscheinlichkeiten der beiden häufigsten Buchstaben e und t: 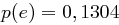 und
und 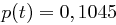 und somit
und somit 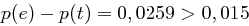 . Es kann also mit großer Wahrscheinlichkeit in einem langen Text zwischen
. Es kann also mit großer Wahrscheinlichkeit in einem langen Text zwischen 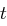 und
und 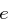 unterschieden werden und die Cäsar-Chiffre mit Hilfe der Häufigkeitsanalyse geknackt werden.
unterschieden werden und die Cäsar-Chiffre mit Hilfe der Häufigkeitsanalyse geknackt werden.
Eine zweite Möglichkeit, Cäsar-Chiffren über dem Alphabet 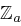 durch eine Häufigkeitsanalyse zu brechen, ist die folgende. Es sei
durch eine Häufigkeitsanalyse zu brechen, ist die folgende. Es sei 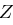 eine Zufallsvariable mit der Verteilung
eine Zufallsvariable mit der Verteilung  wobei
wobei 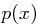 die Wahrscheinlichkeit für das Auftreten des Buchstaben
die Wahrscheinlichkeit für das Auftreten des Buchstaben 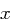 im Klartext ist. Weiterhin seien
im Klartext ist. Weiterhin seien  die beobachteten relativen Häufigkeiten der Buchstaben im Kryptogramm. Bei Schlüssel
die beobachteten relativen Häufigkeiten der Buchstaben im Kryptogramm. Bei Schlüssel 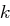 ist
ist 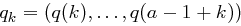 (Indexrechnung modulo
(Indexrechnung modulo 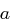 ) die Buchstabenverteilung im Klartext. Die Idee bei der Analyse besteht darin, ein
) die Buchstabenverteilung im Klartext. Die Idee bei der Analyse besteht darin, ein 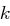 zu bestimmen, bei dem die euklidische Norm
zu bestimmen, bei dem die euklidische Norm
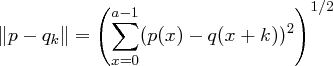
minimal wird, und damit
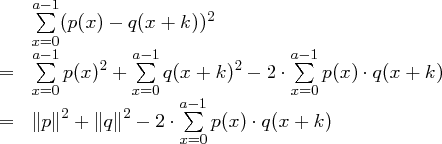
minimal ist. Da 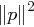 und
und 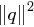 für jedes
für jedes 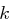 konstant sind, reicht es, den Ausdruck
konstant sind, reicht es, den Ausdruck
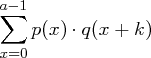
zu maximieren. Für große 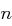 gilt mit einer Wahrscheinlichkeit von fast
gilt mit einer Wahrscheinlichkeit von fast 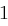 , dass
, dass 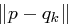 klein ist, wenn
klein ist, wenn 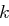 korrekt ist, sowie dass
korrekt ist, sowie dass 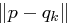 groß ist, wenn
groß ist, wenn 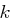 nicht korrekt ist.
nicht korrekt ist.
Aufgabe 1
Gegeben sei eine Cäsar-Chiffre bei beliebigem Modulus 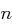 . Ein Angreifer kenne nur einige Kryptogramme
. Ein Angreifer kenne nur einige Kryptogramme 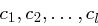 .
.
Diskutieren Sie in nachfolgenden Situationen, ob der Angreifer die Kryptogramme entschlüsseln kann:
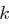 und den Modulus
und den Modulus 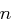 .
.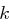 , aber nicht den Modulus
, aber nicht den Modulus 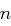 .
.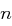 , aber nicht den Schlüssel
, aber nicht den Schlüssel 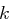 .
.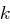 noch Modulus
noch Modulus 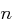 .
.Wie sind die Punkte 1. bis 4. zu beantworten, wenn der Angreifer für das Kryptogramm 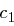 (und nur für dieses) den entsprechenden Klartext kennt?
(und nur für dieses) den entsprechenden Klartext kennt?
Aufgabe 2
Diskutieren Sie Kryptosysteme in Analogie zur Cäsar-Chiffre, die die folgende Chiffrierfunktion 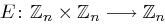 mit
mit 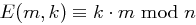 verwenden; speziell hinsichtlich der geeigneten Parameterwahl.
verwenden; speziell hinsichtlich der geeigneten Parameterwahl.
Wie ändert sich die Situation, wenn man Chiffrierfunktionen der Form 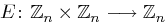 mit
mit 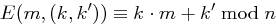 verwendet?
verwendet?
Aufgabe 3
Überlegen Sie sich ein Kryptosystem in Analogie zur Cäsar-Chiffre, das auf konsekutiven Paaren von Buchstaben operiert.
Aufgabe 4
Gegeben ist eine Cäsar-Chiffre über dem endlichen Alphabet 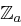 . Bei einem ciphertext-only-attack erhalten Sie genau einen Chiffratbuchstaben
. Bei einem ciphertext-only-attack erhalten Sie genau einen Chiffratbuchstaben 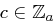 . Gemäß der Gleichverteilung raten Sie zufällig einen Schlüssel
. Gemäß der Gleichverteilung raten Sie zufällig einen Schlüssel 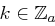 . Nach Ihrer Wahl erfahren Sie, dass der Buchstabe
. Nach Ihrer Wahl erfahren Sie, dass der Buchstabe 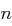 mit
mit 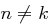 nicht der Schlüssel ist. Sie haben nun die Möglichkeit, Ihre ursprüngliche Wahl einmalig zu revidieren. Würden Sie diese Möglichkeit wahrnehmen?
nicht der Schlüssel ist. Sie haben nun die Möglichkeit, Ihre ursprüngliche Wahl einmalig zu revidieren. Würden Sie diese Möglichkeit wahrnehmen?