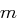 wieder "OTTO KOMMT" und das Schlüsselwort
wieder "OTTO KOMMT" und das Schlüsselwort 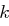 "KEYWORD", so erhalten wir als Chiffrat
"KEYWORD", so erhalten wir als Chiffrat  die Zeichenkette "YXRKYEPWX". Dabei haben wir unter Nutzung der Zuordnung
die Zeichenkette "YXRKYEPWX". Dabei haben wir unter Nutzung der Zuordnung| Cäsar-Chiffre | Hill-Chiffre |
Im 16. Jahrhundert wurde von Blaise de Vigenère eine Verschiebechiffre vorgeschlagen, bei der jedes Zeichen im Klartext je nach Position verschieden weit verschoben wird. Diese Verschiebung wird dabei über ein Schlüsselwort definiert. Am besten versteht man das Prinzip anhand eines Beispiels:
Lautet der Klartext 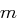 wieder "OTTO KOMMT" und das Schlüsselwort
wieder "OTTO KOMMT" und das Schlüsselwort 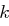 "KEYWORD", so erhalten wir als Chiffrat
"KEYWORD", so erhalten wir als Chiffrat  die Zeichenkette "YXRKYEPWX". Dabei haben wir unter Nutzung der Zuordnung
die Zeichenkette "YXRKYEPWX". Dabei haben wir unter Nutzung der Zuordnung
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
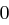 |
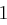 |
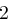 |
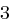 |
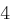 |
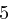 |
 |
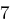 |
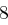 |
 |
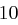 |
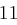 |
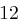 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
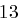 |
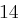 |
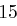 |
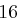 |
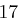 |
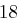 |
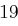 |
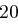 |
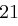 |
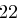 |
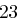 |
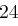 |
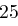 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
den Klartext zunächst in die Zahlenfolge 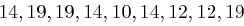 umgewandelt. Die gleiche Prozedur wird mit dem Schlüsselwort vorgenommen, so dass man die Folge
umgewandelt. Die gleiche Prozedur wird mit dem Schlüsselwort vorgenommen, so dass man die Folge 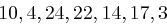 erhält. Man addiert nun die Folgen komponentenweise, also
erhält. Man addiert nun die Folgen komponentenweise, also 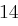 und
und 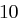 ,
,  und
und 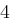 ,
, 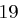 und
und 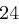 usw., jeweils modulo
usw., jeweils modulo 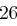 und erhält die Folge
und erhält die Folge 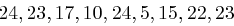 , aus der sich wieder mit obiger Tabelle das Chiffrat ableiten lässt. Zusammengefasst erhalten wir bei Schlüssellänge
, aus der sich wieder mit obiger Tabelle das Chiffrat ableiten lässt. Zusammengefasst erhalten wir bei Schlüssellänge 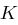 :
:
|
|
|
|
|
|
|
|
|
|
|
|
| unverschlüsselt | O | T | T | O | K | O | M | M | T | |
|
|
|
|
|
|
|
|
|
|
|
|
 |
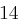 |
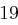 |
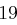 |
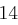 |
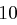 |
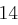 |
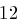 |
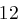 |
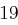 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
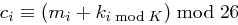 |
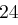 |
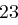 |
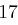 |
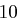 |
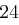 |
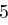 |
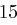 |
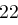 |
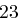 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| verschlüsselt | Y | X | R | K | Y | F | P | W | X | |
|
|
|
|
|
|
|
|
|
|
|
|
Wir wollen nun das Prinzip der Vigenère-Chiffre formalisieren.
Die Verschlüsselung einer Nachricht erfolgt buchstabenweise, wobei die 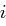 -te Stelle im Klartext, also
-te Stelle im Klartext, also 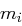 , mit dem Teilschlüssel
, mit dem Teilschlüssel 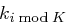 verschlüsselt wird. Der Wert von
verschlüsselt wird. Der Wert von 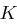 ist die Länge des Schlüssels, das heißt die Anzahl Buchstaben des Schlüsselworts
ist die Länge des Schlüssels, das heißt die Anzahl Buchstaben des Schlüsselworts 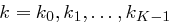 . Dabei entsprechen
. Dabei entsprechen 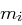 und
und 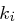 bereits den Zahlenrepräsentationen der Buchstaben des Schlüsselwortes oder des Klartextes nach der Zuordnung in obiger Tabelle. Für die Verschlüsselung des
bereits den Zahlenrepräsentationen der Buchstaben des Schlüsselwortes oder des Klartextes nach der Zuordnung in obiger Tabelle. Für die Verschlüsselung des 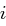 -ten Buchstabens im Klartext gilt also
-ten Buchstabens im Klartext gilt also
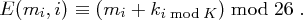
Die Entschlüsselung erfolgt nun bei vorliegendem Chiffrat 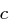 analog in der Form
analog in der Form
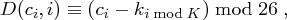
denn es gilt
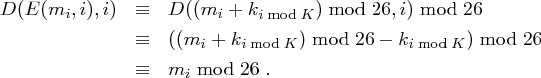
Aufgabe 1
Eine Variante der Vigenère-Chiffre ist die selbstentschlüsselnde Beaufort-Chiffre, die wie folgt definiert ist:
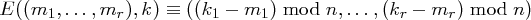
für einen Schlüssel  und eine Nachricht
und eine Nachricht  . Die Chiffrier- und die Dechiffrierfunktion sind also identisch, resp. ihre eigene Inverse.
. Die Chiffrier- und die Dechiffrierfunktion sind also identisch, resp. ihre eigene Inverse.
Das Kryptogramm "CJUJ LAFY TCTU LTKG" wurde für 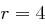 und
und 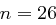 mit dem Schlüssel "EASY" chiffriert. Finden Sie den Klartext.
mit dem Schlüssel "EASY" chiffriert. Finden Sie den Klartext.