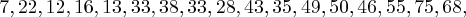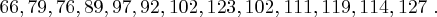Klassische Kryptographie
Übungen
Als Klassische Chiffren bezeichnet man alle bis etwa 1950 entwickelten und benutzten Verfahren.
Von diesen werden hier nur diejenigen vorgestellt, die für das Verständnis der modernen Verfahren notwendig oder hilfreich sind. Alle hier vorgestellten Chiffren arbeiten mit mathematischen Methoden auf einem endlichen Alphabet.
Schon im ersten Jahrhundert vor Christus wurden Nachrichten zu dem Zweck verschlüsselt, dass Dritte keinen Einblick in die übermittelte Information erhalten. Dabei kam eine Chiffre zum Einsatz, die wir heute als Cäsar-Chiffre bezeichnen. Dieses frühe Kryptosystem ist sehr einfach aufgebaut, indem jeder Buchstabe durch genau einen anderen Buchstaben des Alphabets zyklisch ersetzt wird. Genauer wurde jeder Buchstabe des Alphabets um drei Positionen verschoben. Die dahinter stehende Mathematik basiert also auf einfacher Addition modulo 26. Das heißt wir rechnen wie beim Teilen von ganzen Zahlen mit Rest.
In der Folge wurden auch andere ähnlich einfach aufgebaute Chiffren entworfen. So kann man sich überlegen, durch einen Schritt mehrere aufeinander folgende Buchstaben mit diesem Verfahren zu verschlüsseln, wobei der Versatz unterschiedlich gewählt wird. Diese Verfahren bezeichnet man als Vigenère-Chiffre, benannt nach Blaise de Vigenère (16. Jahrhundert).
Derartige Verfahren, bei denen jedes Zeichen des Klartextes durch ein anderes ersetzt wird, nennen wir Substitutionschiffren. Dabei unterscheiden wir monoalphabetische und polyalphabetische Chiffren. Unter ersteren (etwa Cäsar-Chiffre) versteht man, dass jedes Klartextzeichen immer auf das gleiche Geheimtextzeichen abgebildet wird. Ist dies nicht der Fall, etwa bei Verschlüsselung von Buchstabenkombinationen in Blöcken - sog. Block Chiffren, handelt es sich um eine polyalphabetische Chiffre (beispielsweise Vigenère-Chiffre oder die Playfair-Chiffre).
Ein anderer Ansatz für polyalphabetische Chiffren nutzt die Matrixmultiplikation zur Verschlüsselung von Klartextblöcken aus, indem mehrere Zeichen als Vektor interpretiert werden, der mit einer Schlüsselmatrix multipliziert ein Chiffrat liefert. Für die entsprechende Entschlüsselung ist die Multiplikation mit der Inversen der Schlüsselmatrix nötig, so dass nur invertierbare Matrizen verwendet werden können. Das beschriebene Verfahren bezeichnen wir als Hill-Chiffre.
Diese Formen der Verschlüsselung können sehr leicht gebrochen werden, so dass es heute keine ernsthafte praktische Anwendung für derartige Verfahren gibt. So kann man für die Cäsar-Chiffre alle möglichen Verschiebungen systematisch durchprobieren, bis ein lesbarer Text entsteht. Ist das Alphabet zu groß zum Probieren, so bietet sich eine statistische Analyse an, denn die Häufigkeiten von Buchstaben in deutschen Texten variieren kaum. So kann man die Häufigkeiten aller Buchstaben im Geheimtext bestimmen, um diese mit den bekannten mittleren Häufigkeiten in deutschen Texten zu vergleichen.
Wir führen einige grundlegende Methoden der Kryptoanalyse auf. Diese sind:
- Probable Word Methode.
Diese ist eine heuristische Methode, die nach häufig vorkommenden Wörtern oder Ausdrücken wie "Sehr geehrte Damen und Herren" sucht.
- Vollständige Suche.
Bei der vollständigen Suche werden alle möglichen Schlüssel auf das Kryptogramm angewendet. Bei einem known plaintext attack werden mit dieser Methode alle passenden Schlüssel gefunden, während bei einem ciphertext only attack alle Schlüssel gefunden werden, die zu sinnvollen Texten führen. Um eine vollständige Suche zu verhindern, sollte die Schlüsselmenge sehr groß sein, beispielsweise benutzt DES (Data Encryption Standard) 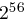 Schlüssel.
Schlüssel.
- Strukturelle Zerlegung des Schlüsselraums.
Falls sich die Schlüssel, beispielsweise 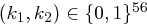 eines Kryptosystems separieren lassen, also getrennt nach
eines Kryptosystems separieren lassen, also getrennt nach 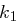 und
und 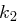 gesucht werden kann, wird das System unsicherer. Hängt zum Beispiel die erste Hälfte des Kryptogramms ausschließlich von
gesucht werden kann, wird das System unsicherer. Hängt zum Beispiel die erste Hälfte des Kryptogramms ausschließlich von 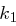 und die zweite Hälfte ausschließlich von
und die zweite Hälfte ausschließlich von 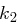 ab, so verringert sich die Anzahl der Möglichkeiten sehr stark. Nehmen wir an, dass
ab, so verringert sich die Anzahl der Möglichkeiten sehr stark. Nehmen wir an, dass 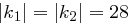 ist, dann verringert sich die Anzahl der durchzuführenden Tests von
ist, dann verringert sich die Anzahl der durchzuführenden Tests von 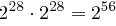 auf
auf 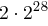 . Jedes Kryptogrammbit sollte daher möglichst von allen Schlüsselbits abhängen.
. Jedes Kryptogrammbit sollte daher möglichst von allen Schlüsselbits abhängen.
- Sprachstatistik.
Die zu verschlüsselnden Nachrichten sind im Allgemeinen strukturiert und enthalten Standardredewendungen, entsprechen einem bestimmten Dateiformat oder die Häufigkeiten der in ihnen vorkommenden Buchstaben entsprechen bekannten Regeln. Diese Eigenschaft kann bei der Kryptoanalyse ausgenutzt werden, indem Häufigkeitstabellen für Buchstaben, Buchstabenpaare (Digramme) oder -tripel (Trigramme) erstellt werden. Nach dem Gesetz der großen Zahlen werden diese Häufigkeiten bei langen Texten approximiert. Ein Beispiel für diese Art der Analyse wird im Abschnitt über die Cäsar-Chiffre gezeigt.
Übungen
Aufgabe 1
Sie haben den Geheimtext "OFJDFOHFXOL" abgehört und wissen, dass er mit einer affin linearen Chiffre (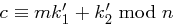 ) der Blocklänge 1 im 27-Zeichen-Alphabet der englischen Sprache kodiert wurde (Leerzeichen = 26). Weiterhin ist Ihnen der Anfang "I " ("I" gefolgt von einem Leerzeichen) bekannt. Finden Sie den Schlüssel und dekodieren Sie die Nachricht.
) der Blocklänge 1 im 27-Zeichen-Alphabet der englischen Sprache kodiert wurde (Leerzeichen = 26). Weiterhin ist Ihnen der Anfang "I " ("I" gefolgt von einem Leerzeichen) bekannt. Finden Sie den Schlüssel und dekodieren Sie die Nachricht.
Aufgabe 2
Bei einem Kryptosystem sei für 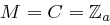 und
und 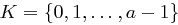 eine Verschlüsselungsfunktion
eine Verschlüsselungsfunktion 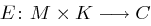 gegeben durch
gegeben durch 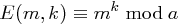 für
für 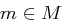 und
und 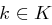 .
.
Ist es kryptographisch sinnvoll, für den Parameter 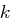 gerade Zahlen zu wählen?
gerade Zahlen zu wählen?
Aufgabe 3
Auf den Webseiten des BND findet man als Chiffrat folgende Zahlenfolge:
Welche Nachricht wurde hier verschlüsselt?
Link zu den Lösungen
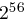 Schlüssel.
Schlüssel.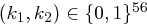 eines Kryptosystems separieren lassen, also getrennt nach
eines Kryptosystems separieren lassen, also getrennt nach 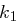 und
und 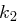 gesucht werden kann, wird das System unsicherer. Hängt zum Beispiel die erste Hälfte des Kryptogramms ausschließlich von
gesucht werden kann, wird das System unsicherer. Hängt zum Beispiel die erste Hälfte des Kryptogramms ausschließlich von 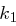 und die zweite Hälfte ausschließlich von
und die zweite Hälfte ausschließlich von 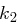 ab, so verringert sich die Anzahl der Möglichkeiten sehr stark. Nehmen wir an, dass
ab, so verringert sich die Anzahl der Möglichkeiten sehr stark. Nehmen wir an, dass 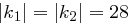 ist, dann verringert sich die Anzahl der durchzuführenden Tests von
ist, dann verringert sich die Anzahl der durchzuführenden Tests von 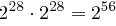 auf
auf 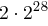 . Jedes Kryptogrammbit sollte daher möglichst von allen Schlüsselbits abhängen.
. Jedes Kryptogrammbit sollte daher möglichst von allen Schlüsselbits abhängen.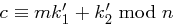 ) der Blocklänge 1 im 27-Zeichen-Alphabet der englischen Sprache kodiert wurde (Leerzeichen = 26). Weiterhin ist Ihnen der Anfang "I " ("I" gefolgt von einem Leerzeichen) bekannt. Finden Sie den Schlüssel und dekodieren Sie die Nachricht.
) der Blocklänge 1 im 27-Zeichen-Alphabet der englischen Sprache kodiert wurde (Leerzeichen = 26). Weiterhin ist Ihnen der Anfang "I " ("I" gefolgt von einem Leerzeichen) bekannt. Finden Sie den Schlüssel und dekodieren Sie die Nachricht.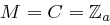 und
und 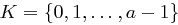 eine Verschlüsselungsfunktion
eine Verschlüsselungsfunktion 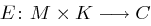 gegeben durch
gegeben durch 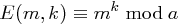 für
für 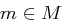 und
und 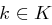 .
.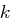 gerade Zahlen zu wählen?
gerade Zahlen zu wählen?