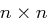 -Matrizen über
-Matrizen über 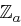 benutzt, das heißt über den ganzen Zahlen
benutzt, das heißt über den ganzen Zahlen 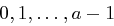 . Dabei entspricht der Parameter
. Dabei entspricht der Parameter 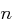 der Blocklänge. Das Inverse einer Matrix
der Blocklänge. Das Inverse einer Matrix 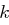 existiert genau dann, wenn gilt
existiert genau dann, wenn gilt 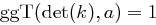 .
.| Vigenère-Chiffre | Playfair-Chiffre |
Verschlüsselung Entschlüsselung Angriffe auf Hill-Chiffren Beispiel Übungen
Die Hill-Chiffren gehören zu den Blockchiffren, das heißt es werden jeweils Klartextblöcke einer bestimmten Länge zu Chiffraten einer bestimmten Länge verschlüsselt, wobei speziell bei Hill-Chiffren die Länge eines Klartextblocks gleich der Länge des zugehörigen Chiffrats ist. Als Schlüsselmenge wird die Menge der invertierbaren 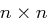 -Matrizen über
-Matrizen über 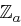 benutzt, das heißt über den ganzen Zahlen
benutzt, das heißt über den ganzen Zahlen 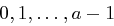 . Dabei entspricht der Parameter
. Dabei entspricht der Parameter 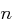 der Blocklänge. Das Inverse einer Matrix
der Blocklänge. Das Inverse einer Matrix 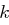 existiert genau dann, wenn gilt
existiert genau dann, wenn gilt 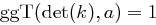 .
.
Für einen gegebenen Buchstaben im Klartext wird zunächst anhand der folgenden Tabelle seine Position im Alphabet bestimmt. Das heißt dem 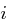 -ten Buchstaben im Klartext wird eine Zahl
-ten Buchstaben im Klartext wird eine Zahl 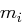 aus
aus 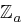 zugewiesen, wie es für
zugewiesen, wie es für 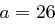 in der folgenden Tabelle illustriert ist.
in der folgenden Tabelle illustriert ist.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
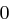 |
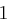 |
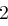 |
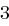 |
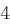 |
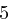 |
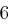 |
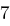 |
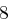 |
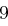 |
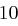 |
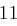 |
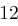 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
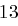 |
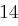 |
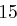 |
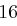 |
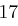 |
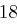 |
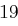 |
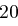 |
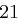 |
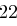 |
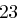 |
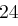 |
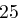 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sei 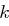 die Schlüsselmatrix und
die Schlüsselmatrix und 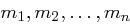 ein Nachrichtenblock, der als Spaltenvektor
ein Nachrichtenblock, der als Spaltenvektor
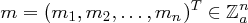
interpretiert wird. Dann ergibt sich das Chiffrat 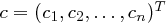 aufgrund der Matrix-Vektor Multiplikation
aufgrund der Matrix-Vektor Multiplikation
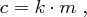
wobei Addition und Multiplikation in 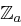 geschieht.
geschieht.
Bestimmt man zur Matrix 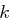 die inverse Matrix
die inverse Matrix 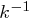 , also eine Matrix der Form
, also eine Matrix der Form
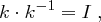
wobei 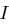 die Einheitsmatrix ist (alle Hauptdiagonalelemente sind gleich Eins und die restlichen Einträge gleich Null), dann lässt sich aus dem Chiffrat
die Einheitsmatrix ist (alle Hauptdiagonalelemente sind gleich Eins und die restlichen Einträge gleich Null), dann lässt sich aus dem Chiffrat 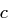 die ursprüngliche Nachricht
die ursprüngliche Nachricht 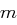 wie folgt bestimmen:
wie folgt bestimmen:
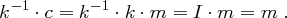
Wir wollen kurz zwei mögliche Angriffe auf die Hill-Chiffre beschreiben. Die erste Möglichkeit ist ein chosen plaintext attack. Mit diesem Angriff sind Hill-Chiffren leicht zu brechen, denn wenn man die 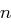 Einheitsvektoren
Einheitsvektoren 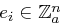 als Nachrichten wählt, so erhält man mit
als Nachrichten wählt, so erhält man mit 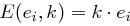 die
die 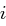 -te Spalte der Matrix
-te Spalte der Matrix 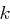 .
.
Die zweite Methode ist ein known plaintext attack. Wenn 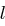 Klartexte
Klartexte  und die zugehörigen Kryptogramme
und die zugehörigen Kryptogramme  , alle aus
, alle aus 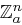 , zur Verfügung stehen, können wir hoffen, dass
, zur Verfügung stehen, können wir hoffen, dass  oder
oder  ein Erzeugendensystem von
ein Erzeugendensystem von 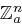 bilden. Es sollte also zumindest
bilden. Es sollte also zumindest 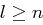 gelten, um den Angriff durchzuführen. Wir benutzen die Ansätze
gelten, um den Angriff durchzuführen. Wir benutzen die Ansätze
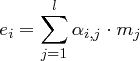
bzw.
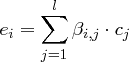
jeweils für 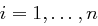 und versuchen, eines der beiden Gleichungssysteme nach den Unbekannten
und versuchen, eines der beiden Gleichungssysteme nach den Unbekannten 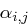 bzw.
bzw. 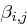 aufzulösen (etwa mit dem Eliminationsverfahren von Gauss). Gelingt dies, so können wir danach mit
aufzulösen (etwa mit dem Eliminationsverfahren von Gauss). Gelingt dies, so können wir danach mit
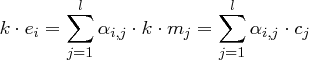
bzw.
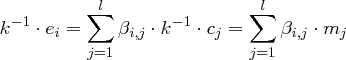
die 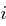 -te Spalte der Matrix
-te Spalte der Matrix 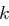 bzw. der Matrix
bzw. der Matrix 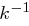 berechnen.
berechnen.
Wir wollen uns noch kurz überlegen, wieviele Klartext/Kryptogramm-Paare wir benötigen, um die Matrix 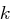 bzw. ihre inverse Matrix
bzw. ihre inverse Matrix 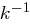 bestimmen zu können, d.h. wie viele solcher Paare nötig sind, um wie besprochen ein Erzeugendensystem zu erhalten. Dazu nehmen wir an, dass die Klartexte unabhängig und gleichverteilt gewählt werden.
bestimmen zu können, d.h. wie viele solcher Paare nötig sind, um wie besprochen ein Erzeugendensystem zu erhalten. Dazu nehmen wir an, dass die Klartexte unabhängig und gleichverteilt gewählt werden.
Sei 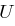 ein linearer Unterraum von
ein linearer Unterraum von 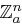 mit
mit 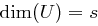 . Die Zufallsgröße
. Die Zufallsgröße 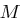 sei die Zufallsgröße für das Ziehen eines Klartextes. Für jeden festen Klartext
sei die Zufallsgröße für das Ziehen eines Klartextes. Für jeden festen Klartext 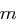 ergibt sich
ergibt sich 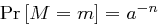 sowie
sowie 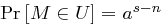 , da die Anzahl der Elemente in
, da die Anzahl der Elemente in 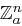 gleich
gleich 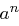 ist und jeder
ist und jeder 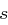 -dimensionale lineare Unterraum von
-dimensionale lineare Unterraum von 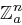 genau
genau 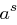 viele Elemente enthält.
viele Elemente enthält.
Als nächstes betrachten wir die Zufallsvariable 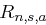 , die die Anzahl zufällig gezogener Klartexte angibt, bis zum ersten Mal
, die die Anzahl zufällig gezogener Klartexte angibt, bis zum ersten Mal 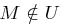 ist. Aufgrund der Gleichverteilung der Klartexte hängt der Wert von
ist. Aufgrund der Gleichverteilung der Klartexte hängt der Wert von 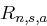 nicht von der speziellen Wahl des Unterraumes
nicht von der speziellen Wahl des Unterraumes 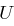 ab und es ergibt sich
ab und es ergibt sich
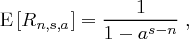
da 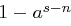 die Wahrscheinlichkeit ist, bei einmaligem Ziehen eines Klartextes nicht im Unterraum zu landen und der Kehrwert der Wahrscheinlichkeit die erwartete Anzahl an Zufallsexperimenten ist, bis das Ereignis zum ersten Mal eintritt.
die Wahrscheinlichkeit ist, bei einmaligem Ziehen eines Klartextes nicht im Unterraum zu landen und der Kehrwert der Wahrscheinlichkeit die erwartete Anzahl an Zufallsexperimenten ist, bis das Ereignis zum ersten Mal eintritt.
Nun betrachten wir die erwartete Anzahl an Zufallsexperimenten 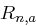 , um einen
, um einen 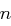 -dimensionalen Unterraum, also den ganzen Raum
-dimensionalen Unterraum, also den ganzen Raum 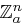 , zu erzeugen. Dazu müssen
, zu erzeugen. Dazu müssen 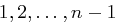 dimensionale Unterräume und schließlich der
dimensionale Unterräume und schließlich der 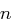 -dimensionale Unterraum erzeugt werden. Er ergibt sich also
-dimensionale Unterraum erzeugt werden. Er ergibt sich also
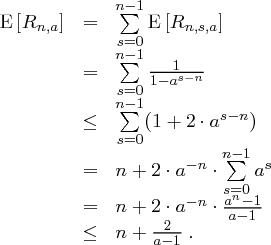
Man benötigt also wenigstens 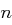 , aber im Mittel höchstens
, aber im Mittel höchstens 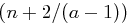 Klartext/Kryptogramm-Paare, um die Matrix
Klartext/Kryptogramm-Paare, um die Matrix 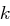 ermitteln zu können. Gehen wir beispielsweise von einer Blocklänge von
ermitteln zu können. Gehen wir beispielsweise von einer Blocklänge von 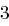 aus und dem
aus und dem 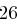 -Zeichen-Alphabet, dann ergibt sich
-Zeichen-Alphabet, dann ergibt sich 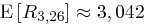 . Schließlich können wir mit der Markov-Ungleichung, die für nichtnegative Zufallsvariablen
. Schließlich können wir mit der Markov-Ungleichung, die für nichtnegative Zufallsvariablen 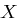 und reelle Zahlen
und reelle Zahlen 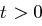 besagt
besagt

abschätzen, wie groß die Wahrscheinlichkeit ist, in diesem Fall mindestens 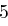 Paare zu benötigen, diese ergibt sich als höchstens
Paare zu benötigen, diese ergibt sich als höchstens 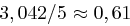 .
.
Verwenden wir die invertierbare Matrix
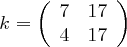
über 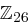 zur Verschlüsselung der durch den Buchstaben X auf geradzahlige Länge ergänzten Nachricht "OTTO KOMMT", aus der zunächst die Vektoren
zur Verschlüsselung der durch den Buchstaben X auf geradzahlige Länge ergänzten Nachricht "OTTO KOMMT", aus der zunächst die Vektoren
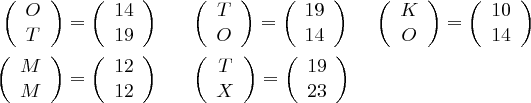
erstellt werden, so erhalten wir die Vektoren
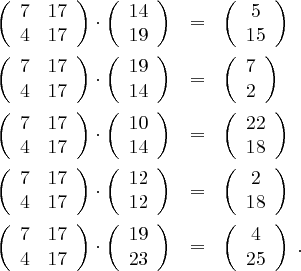
Das Chiffrat lautet also nach einer Rückumwandlung in Buchstaben "FPHC WSCSEZ".
Aufgabe 1
Bekannt sei 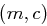 = ("TURING", "UBIXGT").
= ("TURING", "UBIXGT").
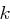 bzw. deren Inverse
bzw. deren Inverse 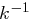 und entschlüsseln Sie den restlichen Geheimtext "ENERHLNHAHRM".
und entschlüsseln Sie den restlichen Geheimtext "ENERHLNHAHRM".
Aufgabe 2
Bekannt seien folgende 7 plaintext/ciphertext - Paare:
| HAV | EDI | FFE | REN | TOB | JEC | TIV |
| QQX | DUK | ITS | GAD | UWH | XRM | SWL |
Brechen Sie in einem Known-Plaintext-Angriff die Hill-Chiffre mit der Blocklänge 3 vollständig. Finden Sie dazu die Schlüsselmatrix 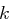 bzw. deren Inverse
bzw. deren Inverse 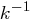 .
.
Aufgabe 3
Gegeben sei eine Hill-Chiffre mit Blocklänge 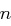 über dem Alphabet
über dem Alphabet 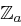 , also
, also 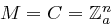 , und mit der Schlüsselmenge
, und mit der Schlüsselmenge 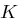 . Bei einer Modifikation dieser Hill-Chiffre nehmen wir als Schlüsselmenge
. Bei einer Modifikation dieser Hill-Chiffre nehmen wir als Schlüsselmenge 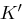 alle Produkte von je zwei Matrizen aus
alle Produkte von je zwei Matrizen aus 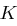 , wobei auch
, wobei auch 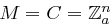 ist. Eine Nachricht
ist. Eine Nachricht 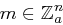 wird verschlüsselt zum Chiffrat
wird verschlüsselt zum Chiffrat 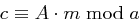 mit Schlüssel
mit Schlüssel 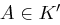 .
.
Vergleichen Sie diese modifizierte Hill-Chiffre mit der normalen Hill-Chiffre.
Aufgabe 4
Gegeben ist eine modifizierte Hill-Chiffre mit Blocklänge 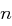 über dem Alphabet
über dem Alphabet 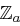 und
und 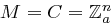 . Die Schlüsselmenge
. Die Schlüsselmenge 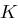 ist nun die Menge aller
ist nun die Menge aller 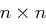 Matrizen
Matrizen 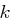 mit Einträgen aus
mit Einträgen aus 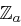 , wobei jede Matrix
, wobei jede Matrix 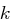 nur auf der Diagonalen von
nur auf der Diagonalen von 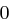 verschiedene Eintrage besitzt und
verschiedene Eintrage besitzt und 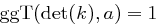 gilt.
gilt.
Diskutieren Sie jeweils einen - für den Angreifer möglichst effizienten - chosen plaintext, chosen ciphertext und known plaintext Angriff auf diese Chiffre.
Aufgabe 5
Gegeben sei eine natürliche Zahl 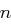 . Zufällig gemäß der Gleichverteilung wird eine natürliche Zahl
. Zufällig gemäß der Gleichverteilung wird eine natürliche Zahl 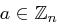 gewählt.
gewählt.
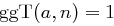 gilt.
gilt.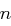 das Produkt zweier verschiedener Primzahlen
das Produkt zweier verschiedener Primzahlen 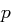 und
und 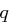 ist. Bei welchen Zahlen
ist. Bei welchen Zahlen 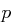 und
und 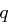 ist diese Wahrscheinlichkeit groß bzw. klein?
ist diese Wahrscheinlichkeit groß bzw. klein?
Aufgabe 6
Bei einer 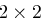 Hill-Chiffre über
Hill-Chiffre über 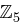 gehören zu den Nachrichten
gehören zu den Nachrichten 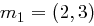 und
und 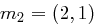 die Chiffrate
die Chiffrate 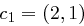 und
und 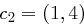 .
.
Berechnen Sie die Verschlüsselungsmatrix 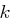 .
.
Aufgabe 7
Die Einträge einer 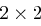 Schlüsselmatrix
Schlüsselmatrix 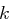 einer Hill-Chiffre über
einer Hill-Chiffre über 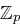 mit einer Primzahl
mit einer Primzahl 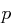 seien einem Angreifer bis auf den Eintrag an der Position
seien einem Angreifer bis auf den Eintrag an der Position 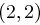 bekannt.
bekannt.
Kann der Angreifer die möglichen Werte für den Eintrag 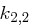 einschränken bzw. diesen eindeutig bestimmen?
einschränken bzw. diesen eindeutig bestimmen?
Aufgabe 8
In einem Kryptosystem mit Nachrichtenmenge 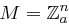 und Chiffratmenge
und Chiffratmenge 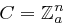 besteht die Schlüsselmenge
besteht die Schlüsselmenge 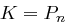 aus allen
aus allen 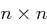 Matrizen
Matrizen 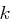 mit Einträgen aus
mit Einträgen aus 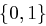 , wobei jede Zeile und jede Spalte aus
, wobei jede Zeile und jede Spalte aus 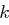 genau eine
genau eine 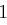 enthält. Die Verschlüsselungsfunktion
enthält. Die Verschlüsselungsfunktion 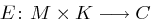 ist gegeben durch
ist gegeben durch 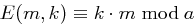 mit
mit  und
und 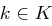 , wobei
, wobei 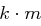 ein Matrix-Vektorprodukt ist und alle Einträge von
ein Matrix-Vektorprodukt ist und alle Einträge von 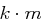 jeweils
jeweils 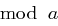 berechnet werden.
berechnet werden.
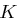 ?
?
Aufgabe 9
Wir erweitern das Kryptosystem mit 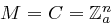 aus der vorherigen Aufgabe dahingehend, dass wir als Schlüsselmenge
aus der vorherigen Aufgabe dahingehend, dass wir als Schlüsselmenge 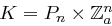 wählen. Die Verschlüsselungsfunktion
wählen. Die Verschlüsselungsfunktion 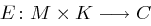 ist definiert durch
ist definiert durch 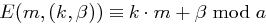 mit
mit 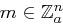 ,
, 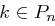 und
und 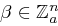 , wobei alle Einträge von
, wobei alle Einträge von 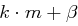 jeweils
jeweils 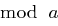 bestimmt werden.
bestimmt werden.
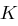 ?
?
Aufgabe 10
Wir betrachten einen chosen plaintext Angriff auf das Kryptosystem aus Aufgabe 8.
Wieviele Nachrichten 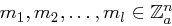 muss ein Angreifer höchstens wählen, um mit Wissen der entsprechenden Chiffrate
muss ein Angreifer höchstens wählen, um mit Wissen der entsprechenden Chiffrate 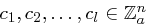 den verwendeten Schlüssel eindeutig ermitteln zu können? Versuchen Sie, einen möglichst kleinen Wert für
den verwendeten Schlüssel eindeutig ermitteln zu können? Versuchen Sie, einen möglichst kleinen Wert für  zu bestimmen.
zu bestimmen.