Buchstaben. Das zugrunde liegende Alphabet ist 
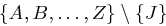. Der Buchstabe J wird im Klartext mit dem Buchstaben I gleichgesetzt.| Hill-Chiffre | Perfekte Sicherheit |
Verschlüsselung Entschlüsselung Beispiel Übungen
Die Playfair-Chiffre, die auf Baron Playfair of St. Andrews (1854) zurückgeht, ist eine polygraphische Substitutionschiffre, das heißt, es werden Blöcke von Buchstaben verschlüsselt. Bei der Playfair-Chiffre bestehen diese Blöcke (sowohl Klartext als auch Chiffrat) aus jeweils Buchstaben. Das zugrunde liegende Alphabet ist 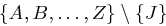. Der Buchstabe J wird im Klartext mit dem Buchstaben I gleichgesetzt.
Der Schlüsselraum der Playfair-Chiffre ist die Menge aller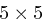 
-Matrizen, wobei jeder Buchstabe aus dem Alphabet genau einmal in jeder Matrix vorkommt. Eine solche Matrix könnte wie folgt aussehen:
Die Verschlüsselung eines Textes geschieht nun auf folgende Weise. Zunächst werden die Buchstaben des Textes beginnend von vorn sukzessive in Zweiergruppen aufgeteilt. Besteht eine Gruppe aus zwei gleichen Buchstaben, dann wird zwischen diese beiden gleichen Buchstaben ein seltener Füllbuchstabe, etwa ein "X", eingefügt und der Text weiter in Zweiergruppen aufgeteilt. Besteht die letzte Gruppe nur aus einem Buchstaben, dann wird zusätzlich der gewählte Füllbuchstabe angehängt.
Wir unterscheiden bei der Kodierung eines Blockes aus zwei Buchstaben folgende drei Fälle:
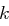. Jeder Buchstabe wird verschlüsselt, indem er durch seinen rechten Nachbarn ersetzt wird. Hat ein Buchstabe keinen rechten Nachbarn, das heißt der zu verschlüsselnde Buchstabe steht in der fünften Spalte der Matrix 
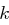, dann wird der Buchstabe der ersten Spalte der Zeile verwendet.
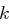. Als Chiffrat werden die Buchstaben verwendet, die genau eine Zeile darunter in der Matrix 
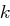enthalten sind. Liegt der zu verschlüsselnde Buchstabe in der letzten Zeile, dann wird der Buchstabe aus der ersten Zeile der Spalte verwendet.
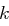. Man geht in der Zeile des ersten Buchstaben zu der Spalte, in der sich der zweite Buchstabe befindet. Der Buchstabe an dieser Position ist das Chiffrat des ersten Buchstaben. Für den zweiten Buchstaben wird analog verfahren.Die Entschlüsselung erfolgt analog zur Verschlüsselung, wobei wir bei Regel 1 jeweils den linken Nachbarn und bei Regel 2 jeweils den oberen Nachbarn wählen. Bei Regel 3 können wir exakt die gleichen Schritte wie bei der Verschlüsselung durchführen.
Der Satz "OTTO KOMMT" soll mit obiger Matrix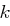 
verschlüsselt werden.
Zunächst wird der Satz in Zweiergruppen aufgeteilt und Gruppen mit gleichen Buchstaben werden durch den Füllbuchstaben "X" getrennt: OT TO KO MX MT
OT: Mit Regel 3 verschlüsselt zu YX
TO: Mit Regel 3 verschlüsselt zu XY
KO: Mit Regel 2 verschlüsselt zu PQ
MX: Mit Regel 1 verschlüsselt zu ZM
MT: Mit Regel 3 verschlüsselt zu HX
Insgesamt erhalten wir als Chiffrat also "YXXYPQZMHX".
Aufgabe 1
Gegeben sei eine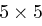 
Playfair Chiffre mit Matrix 
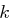. Ein Sender verschlüsselt eine Nachricht zweimal unter Verwendung der gleichen Matrix 
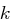, das heißt, er verschlüsselt den Klartext und dann noch einmal das Resultat.
Ist dieses Vorgehen kryptographisch sinnvoll?