 keinerlei Rückschlüsse auf den zugehörigen Klartext ziehen kann.
keinerlei Rückschlüsse auf den zugehörigen Klartext ziehen kann.| Playfair-Chiffre | Moderne Chiffren |
Der Begriff der perfekten Sicherheit wurde von Shannon eingeführt. Shannons Idee bei perfekt sicheren Kryptosystemen war, dass ein Angreifer Oskar aus einem empfangenen Chiffrat  keinerlei Rückschlüsse auf den zugehörigen Klartext ziehen kann.
keinerlei Rückschlüsse auf den zugehörigen Klartext ziehen kann.
Wir nehmen an, dass die Klartexte 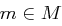 gemäß einer Wahrscheinlichkeitsverteilung
gemäß einer Wahrscheinlichkeitsverteilung 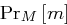 auftreten. Analoges gilt für die verwendeten Schlüssel
auftreten. Analoges gilt für die verwendeten Schlüssel 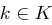 gemäß einer Wahrscheinlichkeitsverteilung
gemäß einer Wahrscheinlichkeitsverteilung 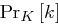 . Dann gilt für den Empfang eines bestimmten Chiffrats
. Dann gilt für den Empfang eines bestimmten Chiffrats 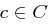 :
:
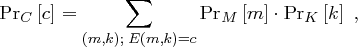
da Klartext und Schlüssel unabhängig voneinander gewählt werden, wobei 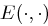 die Chiffrierfunktion ist.
die Chiffrierfunktion ist.
Definition 1 (perfekt sicheres Kryptosystem)
Das eben vorgestellte Kryptosystem heißt perfekt sicher, wenn für alle Paare 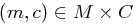 mit
mit 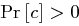 gilt
gilt 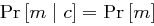 .
.
In perfekt sicheren Systemen ist also bei Vorliegen des Chiffrats 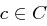 jeder Klartext genauso wahrscheinlich wie er ohne Vorliegen des Chiffrats ist, das heißt, der Gegner erhält aus
jeder Klartext genauso wahrscheinlich wie er ohne Vorliegen des Chiffrats ist, das heißt, der Gegner erhält aus 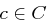 keine Information über den zugehörigen Klartext.
keine Information über den zugehörigen Klartext.
Beispiel 2
Sei 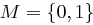 ,
, 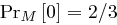 und
und 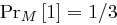 . Weiter sei
. Weiter sei 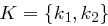 mit
mit 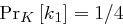 und
und 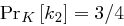 , sowie
, sowie 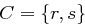 . Für die Verschlüsselungsfunktion
. Für die Verschlüsselungsfunktion 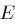 gelte
gelte
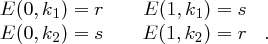
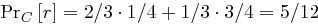 sowie
sowie 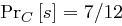 . Weiter ist
. Weiter ist 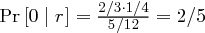 und
und 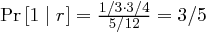 , sowie
, sowie 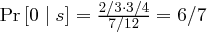 und
und 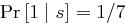 . Das System ist also nicht perfekt sicher.
. Das System ist also nicht perfekt sicher.
Satz 3
Ein perfekt sicheres kryptographisches System hat mindestens soviele Schlüssel wie es Klartexte mit positiver Wahrscheinlichkeit hat.
Beweis Sei 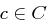 ein Chiffrat mit
ein Chiffrat mit 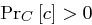 , und
, und 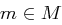 ein Klartext mit
ein Klartext mit 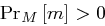 . Dann gilt wegen der perfekten Sicherheit
. Dann gilt wegen der perfekten Sicherheit 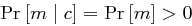 , also existiert ein Schlüssel
, also existiert ein Schlüssel 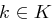 mit
mit 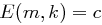 . Wegen der Injektivität von
. Wegen der Injektivität von 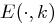 sind die gefundenen Schlüssel paarweise verschieden.
sind die gefundenen Schlüssel paarweise verschieden.
Satz 4
Sei 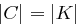 und
und 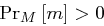 für jeden Klartext
für jeden Klartext 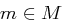 . Das Kryptosystem ist perfekt sicher genau dann, wenn die Wahrscheinlichkeitsverteilung
. Das Kryptosystem ist perfekt sicher genau dann, wenn die Wahrscheinlichkeitsverteilung 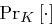 auf der Schlüsselmenge
auf der Schlüsselmenge 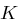 die Gleichverteilung ist und für jedes Paar
die Gleichverteilung ist und für jedes Paar 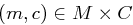 genau ein Schlüssel
genau ein Schlüssel 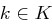 mit
mit 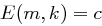 existiert.
existiert.
Beweis Angenommen, das System habe perfekte Sicherheit. Dann gibt es zu jedem Klartext 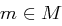 und für jedes Chiffrat
und für jedes Chiffrat 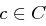 einen Schlüssel
einen Schlüssel 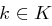 mit
mit 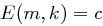 , da ansonsten
, da ansonsten 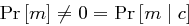 gelten würde. Mit
gelten würde. Mit 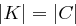 folgt die Eindeutigkeit des Schlüssels
folgt die Eindeutigkeit des Schlüssels 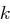 .
.
Sei nun ein Chiffrat 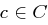 gegeben. Für einen beliebigen Klartext
gegeben. Für einen beliebigen Klartext 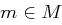 sei
sei 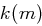 der Schlüssel mit
der Schlüssel mit 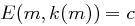 . Dann gilt nach dem Bayesschen Satz:
. Dann gilt nach dem Bayesschen Satz:
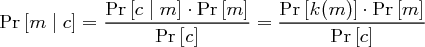
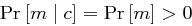 folgt sofort
folgt sofort
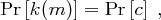
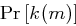 unabhängig von
unabhängig von 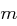 . Da für jeden Schlüssel
. Da für jeden Schlüssel 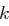 ein Klartext
ein Klartext 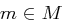 existiert mit
existiert mit 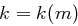 , folgt Gleichverteilung auf
, folgt Gleichverteilung auf 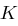 .
.
Angenommen nun, auf 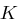 liege Gleichverteilung vor und für alle Paare
liege Gleichverteilung vor und für alle Paare 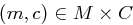 gibt es genau einen Schlüssel
gibt es genau einen Schlüssel 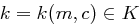 mit
mit 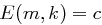 . Dann gilt
. Dann gilt
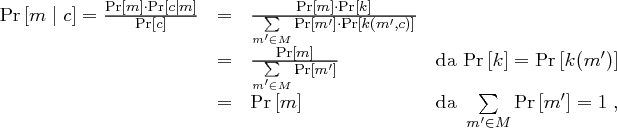
Hill-Chiffre sind nicht perfekt sicher, da Nullvektoren immer zu Nullvektoren verschlüsselt werden. Für 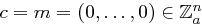 gilt daher
gilt daher 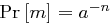 und
und 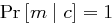 bei Gleichverteilung der Nachrichten in
bei Gleichverteilung der Nachrichten in 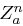 .
.