Beschleunigungsermittlung
Vorgehen
- Ermittlung aller Geschwindigkeiten
- Aufstellen des Satzes von Euler für die Beschleunigung
- Bekannte Größen kennzeichnen
- Beschleunigungen mit bekannter Richtung oder bekanntem Betrag einfach unterstreichen
- Beschleunigungen mit bekannter Richtung und bekanntem Betrag doppelt unterstreichen
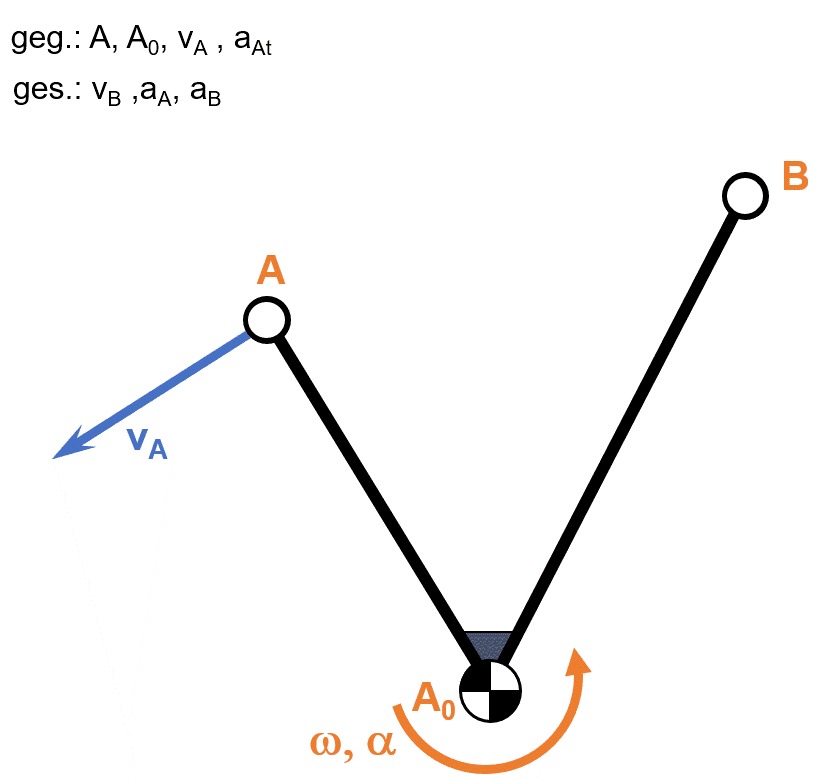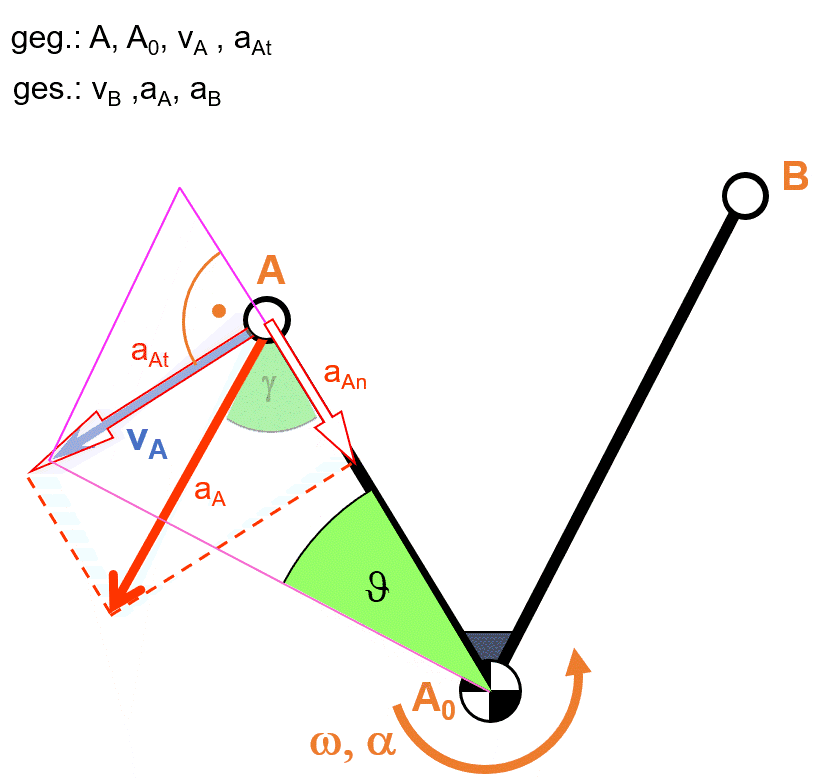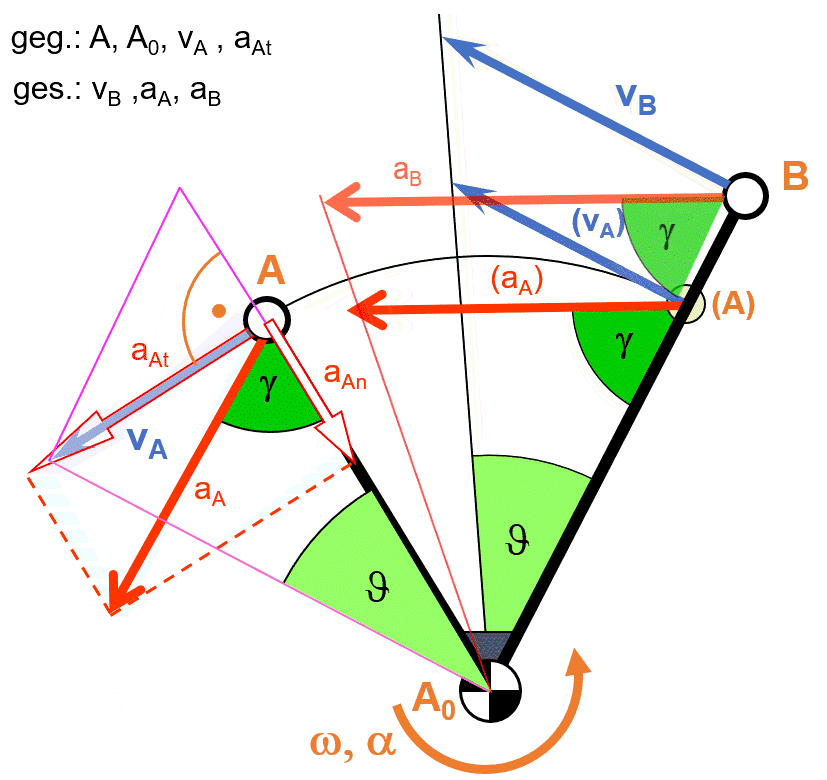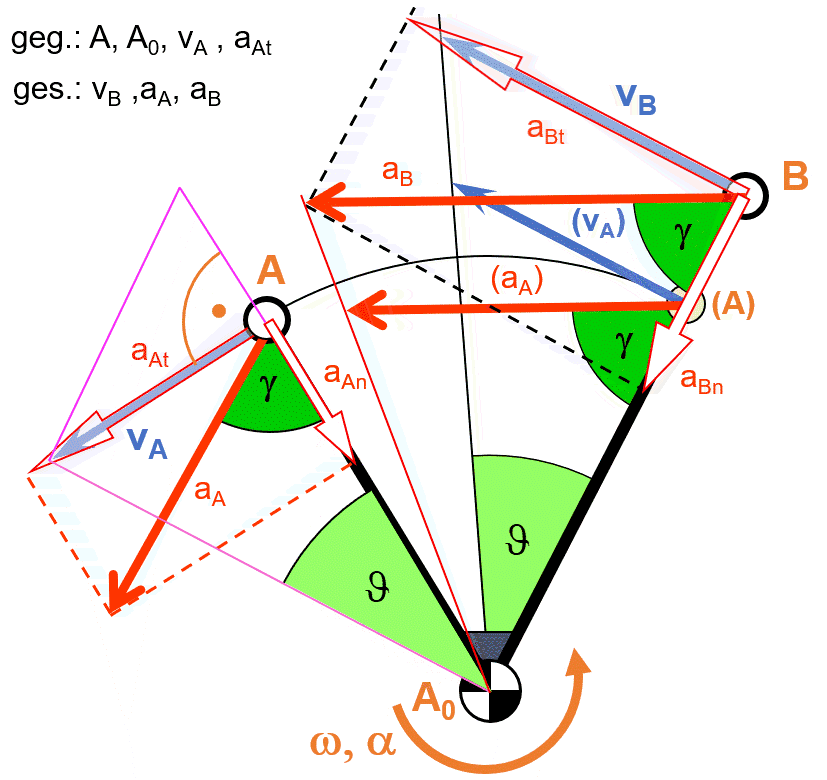
- Überführen der bekannten Beschleunigungen, Richtungen und Beträge in den Beschleunigungsplan
- Einzeichnen der gesuchten Beschleunigung im Beschleunigungsplan
- Umrechnen der gesuchten Beschleunigung mithilfe des Beschleunigungsmaßstabs
Hinweis: Bei der relativen Bewegung dreier Ebenen muss neben den Normal- und Tangentialbeschleunigungen, die Coriolisbeschleunigung berücksichtigt werden. Eine relative Bewegung dreier Ebenen tritt beispielsweise bei einer bewegten Schubgeraden (Kurbelschleife) auf.
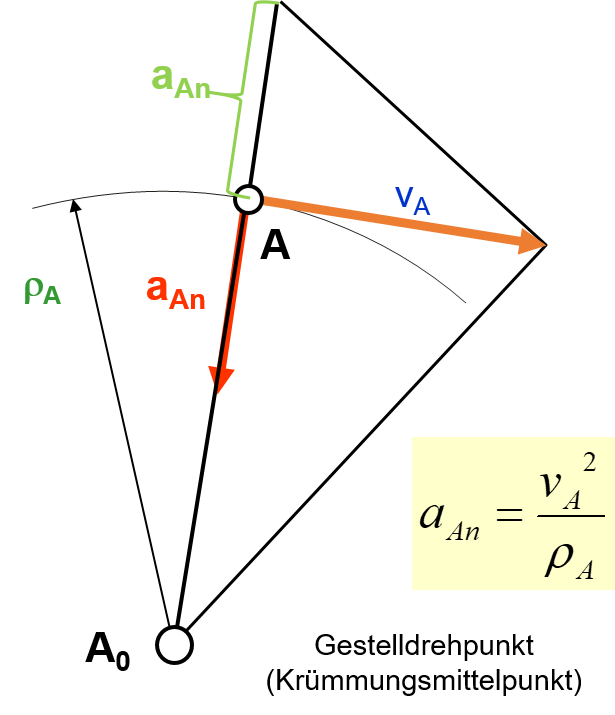
Hinweise: Normalbeschleunigungen können mithilfe des Höhensatzes aus der Geschwindigkeit ermittelt werden. Die Tangentialbeschleunigung ist immer senkrecht zur Normalbeschleunigung gerichtet.
Beispiel Winkelhebel
- Ermittlung der Geschwindigkeit des Punktes
- Wahl des Geschwindigkeitsmaßstabs
- Einzeichnen des Vektors
- Ermittlung der Geschwindigkeit
- Ermittlung der Beschleunigung
- Berechnung des Beschleunigungsmaßstab
- Einzeichnen der Tangentialbeschleunigung
- Einzeichnen der Normal- und Tangentialbeschleunigung des Punktes
Höhensatz