Forschungsprojekte

1. Laufende Projekte
   1. Diffusion und Trapping in begrenzten Flüssigkeitsfilmen und an Oberflächen
   2. Hyperbolizität und Lyapunov-Analyse
   3. Musterbildung in Systemen mit fluktuierender Verzögerung
   4. Stabilität spanender Bearbeitungsprozesse
   5. Chaos in ungeordneten Hamilton-Systemen
   6. Anomaler Transport
   7. Dynamik hysteretischer Systeme
2. Vergangene Projekte
   1. Langzeitverhalten großer dynamischer Systeme
   2. Modellierung schneller chaotischer Freiheitsgrade durch stochastische Prozesse
   3. Untersuchung nichtlinear-dynamischer Effekte in der Instandhaltung
   4. Kontrolle ausgedehnter schneller komplexer Systeme mit raum-zeitlich verzögerter Rückkopplung
   5. Verbesserung der Schnittqualität beim Schneiden mit Wasserabrasivstrahlen durch Methoden der nichtlinearen Dynamik
   6. Analyse verborgener Diffusionsprozesse
   7. Methoden der Systemadaption

Laufende Projekte

Diffusion und Trapping in begrenzten Flüssigkeitsfilmen und an Oberflächen

Förderung im Rahmen der Sächsische Forschergruppe 877 "From Local Constraints to Macroscopic Transport"
Teilbereich P4 "Diffusion and Trapping in Confined Liquid Films and at Interfaces"

Projektleitung: Prof. Dr. Günter Radons

Details finden Sie in der englischen Version dieser Seite und in unserer Arbeitsgruppenbroschüre (PDF) auf den Seiten 18 f. und 20 f.

Hyperbolizität und Lyapunov-Analyse

Musterbildung in Systemen mit fluktuierender Verzögerung

Stabilität spanender Bearbeitungsprozesse

Chaos in ungeordneten Hamilton-Systemen

Anomaler Transport

Dynamik hysteretischer Systeme

Hysterese ist ein weitverbreitetes Phänomen. Man kann es außer in physikalischen und chemischen Zusammenhängen auch in ingenieurwissenschaftlichen, sozialen oder ökonomischen Systemen beobachten. Eine erfolgreich angewandte und weitverbreitete Modellklasse für komplexe Hysterese mit nicht-lokalem Gedächtnis stellt das Preisach-Modell dar.

Unser Interesse liegt zum einen in der Kopplung dynamischer Systeme (iterierte Abbildungen, partielle Differentialgleichungen) mit diesen Modellen und zum anderen in Hysteresemodellen, welche von zufälligen bzw. chaotischen Prozessen getrieben werden. Aktuelle Untersuchungen lieferten bedeutende Einsichten bezüglich des Ursprungs und der Auswirkung des Langzeitgedächtnisses hysteretischer Prozesse.

• G. Radons, Hysteresis-Induced Long-Time Tails, Phys. Rev. Lett. 100, 240602 (2008). Abstract
• Pressemitteilung der TU Chemnitz vom 8. September 2008: Das Gedächtnis von Arbeitslosigkeit und Hochwasser berechnen (PDF)
• Seite 6 f. in unserer Arbeitsgruppenbroschüre (PDF)

Vergangene Projekte

Langzeitverhalten großer dynamischer Systeme

Seit 2006 Einzelförderung durch die DFG. Bis 2005 Bestandteil des interdisziplinärer Sonderforschungsbereich 393 "Numerische Simulation auf massiv parallelen Rechnern":
Projektbereich C "Simulation und Anwendungen in der Physik"
Teilbereich C8 "Langzeitverhalten großer dynamischer Systeme"
http://www.tu-chemnitz.de/sfb393/

Projektleitung: Prof. Dr. Günter Radons
Kontakt: Dr. Hong-liu Yang , Dipl. Phys. Christian Drobniewski

Während nichtlineare dynamische Systeme mit wenigen Freiheitsgraden und kompaktem Phasenraum inzwischen gut verstanden sind, trifft dies für ausgedehnte Systeme oder Systeme mit vielen Freiheitsgraden nicht zu. Neue Aspekte liegen hier insbesondere (a) im Auftreten von raum-zeitlichem Chaos und (b) in dynamischen Phänomenen, wie sie aus der Unordnungsphysik bekannt sind. In beiden Fällen interessiert vor allem das Langzeitverhalten, das jedoch für große Systeme mit konventioneller Rechentechnik schwer zugänglich ist.

Rechendauer (abfallende Kurven) und Orthogonalisierungsgrad (ansteigende Kurven) als Funktion der Prozessorenzahl für das parallelisierte Programm im Cluster CLIC der TU Chemnitz für eine Simulation einer 3d binären Lennard-Jones-Flüssigkeit mit 80 A-Teilchen und 20 B-Teilchen.

Das wissenschaftliche Projektziel liegt in der Aufdeckung der Zusammenhänge zwischen charakteristischen Größen der nichtlinearen Dynamik, wie z.B. Lyapunovspektren, und makroskopischen Größen, wie z.B. Transportkoeffizienten und thermodynamischen Ableitungen in ungeordneten Systemen. Ein interessantes System, das die beiden Aspekte (a) und (b) in sich vereint und das deshalb untersucht werden soll, sind binäre Lennard-Jones-Flüssigkeiten. Hier wird die statische Unordnung in Form eines Glasübergangs selbst generiert, was sich in einem nicht-trivialen Verhalten des Lyapunovspektrums anzudeuten scheint. Ferner zeigt das System nur teilweise verstandene Alterungsphänomene.

Höhenlinien der statischen Korrelationsfunktion S^(αα)(k) für eine 1-d Lennard-Jones-Flüssigkeit (N = 100, L = 1000). Der Kamm bei kleinen k- und λ-Werten (angedeutet durch die gestrichelte Linie) zeigt die Existenz hydrodynamischer Lyapunov-Moden.

Es kommen Methoden aus der Theorie periodischer Orbits, der Molekulardynamik und Techniken, wie das Parallel-Tempern, zum Einsatz. Das Programm kann nur mit Hilfe von äußerst leistungsfähiger Rechentechnik umgesetzt werden und bedeutet eine technische Herausforderung in Bezug auf seine Parallelisierung. Außer für den Periodic-Orbit-Zugang und das Parallel-Tempern ist die Parallelisierung wegen der erforderlichen Systemgrößen notwendig. Probleme, die z.B. bei der Parallel-Implementierung der Berechnung von Lyapunovspektren für hochdimensionale Systeme auftreten können, werden zusammen mit Spezialisten aus der Informatik angegangen.

Modellierung schneller chaotischer Freiheitsgrade durch stochastische Prozesse

Zusammenarbeit mit der Gruppe Nichtlineare Dynamik und Zeitreihenanalyse am Max-Planck-Institut für Physik komplexer Systeme und der Gruppe Dynamical Systems der Queen Mary / University of London gefördert von der Deutschen Forschungsgemeinschaft

Projektleitung: PD Dr. Wolfram Just, Prof. Dr. Holger Kantz, Prof. Dr. Günter Radons
Kontakt: Dr. Katrin Gelfert

Mit dem Ziel einer vereinfachten Modellierung von Systemen mit ausgeprägter Zeitskalentrennung ersetzen wir schnelle chaotische Freiheitsgrade durch stochastische Prozesse. Dieser Fall wird durch die bisher in der Literatur vorliegenden Eliminationsverfahren nicht in systematischer Weise erfasst. Offene Fragestellungen umfassen sowohl eine mathematisch rigorose Analyse als auch praktische Aspekte im Zusammenhang mit der Implementierung. Ziel des Projektes ist es, die Gültigkeit unserer Approximationen im Detail zu studieren, um so die formale Lösung des Problems in ein praktisch nutzbares Verfahren fortzuentwickeln. Dieses Vorhaben stellt einen neuen Ansatz für die Modellierung und effektive Simulation von Systemen mit stark ausgeprägter Zeitskalentrennung dar. Es weckt die Hoffnung auf neuartige Entwicklungen und Fortschritte, beispielsweise in der Klimamodellierung und Molekulardynamik, wo Langzeitsimulationen sich an den langsamen Freiheitsgraden orientieren müssen, während die Integrationsschrittweiten an die schnellen Zeitskalen angepasst sind, die man gerne durch Rauschprozesse ersetzen würde.

Untersuchung nichtlinear-dynamischer Effekte in der Instandhaltung

Projektleitung: Prof. Dr. Berend Denkena , Prof. Dr. Hans Kurt Tönshoff, Prof. Dr. Günter Radons
Kontakt: Dipl. Phys. André Löser

Nichtlinear-dynamische Effekte entstehen in der Instandhaltung u.a. durch stochastisches Auftreten von Maschinenstörungen mit sich dynamisch entwickelnden Ausfallraten, durch Rückkopplungen verschiedener Arbeitsstationen, Abhängigkeiten des Maschinenverhaltens vom Verschleißzustand von Werkzeugen und Maschinenelementen, Instabilitäten der Maschinen durch Störungen und Ausschuss, fehlendem Material und Personal sowie wechselnden Kapazitätsanforderungen. In der Theorie stochastischer oder deterministischer dynamischer Systeme wurden Methoden entwickelt, die es erlauben aus Zeitreihen von beobachtbaren Variablen auf die interessierenden Systemvariablen bzw. Systemzustände zu schließen um z.B. driftende Systemvariable, die Rückschlüsse auf die Zuverlässigkeit erlauben, zu identifizieren.

Die wissenschaftliche Zielsetzung dieses Projekts ist ein Beispiel für die Evaluation, Umsetzung und Weiterentwicklung von existierenden Methoden der nichtlinearen Dynamik an einem technisch relevanten komplexen Prozess, bei dem konventionelle Vorgehensweisen an ihre Grenzen stoßen und nicht zum Ziel führen. Am konkreten Beispiel einer komplexen Transferanlage im Dauerbetrieb und mit hohem Durchsatz soll die Machbarkeit einer automatisierten Prozesskontrolle bzw. -regelung unter Einbeziehung von dynamisch variierenden Zuverlässigkeitsaspekten und daran angepassten Instandhaltungsmaßnahmen aufgezeigt werden.

Kontrolle ausgedehnter schneller komplexer Systeme mit raum-zeitlich verzögerter Rückkopplung

Zusammenarbeit mit der Gruppe "Nichtlineare Spindynamik", Institut für Festkörperphysik, TU Darmstadt und unterstützt von der Deutschen Forschungsgemeinschaft

Projektleitung: Prof. Dr. Hartmut Benner, PD Dr. Wolfram Just, Prof. Dr. Günter Radons

Schwerpunkt des Projektes ist die Kontrolle räumlich ausgedehnter chaotischer Systeme mit Hilfe raum-zeitlich verzögerter Rückkopplung. Es sollen neue und robuste Kontrollmethoden zur Stabilisation schneller raum-zeitlicher Strukturen entwickelt werden. Ausgehend von einer experimentellen Sichtweise werden komplexe elektronische Netzwerke und ferromagnetische Filme von Hauptinteresse sein. Basierend auf analytischen Ansätzen, numerischen Simulationen und echten Experimenten werden wir untersuchen, wie Grenzen, zum Beispiel topologischen Ursprungs, durch die Modifikation der Kontrollmechanismen aufgeweitet werden können. Als eine Anwendung beabsichtigen wir die Stabilisierung von dynamischen Gittern in Yttrium-Eisen-Granat-Filmen oberhalb der ersten Suhl-Schwelle.

Experimentelles Bifurkationsdiagramm für ferromagnetische Resonanz an YIG-Kugeln (ν = 9.26 GHz) in Abhängingkeit vom magnetischen Feld H und der Stärke der einwirkenden Mikrowellen P_in. Die untere Linie kennzeichnet die erste Suhl-Schwelle, die darüber liegenden Linien trennen Bereiche mit unterschiedlichem zeitlichen Verhalten: z.B. Periodenverdopplung (P2, P4), Quasiperiodizität (QP), verschiedene Intermittency Typen (INT II, INT III) oder Chaos.

Verbesserung der Schnittqualität beim Schneiden mit Wasserabrasivstrahlen durch Methoden der nichtlinearen Dynamik

Bis 2005 durch das interdisziplinäres Schwerpunktprogramm der Volkswagenstiftung "Untersuchung nichtlinear-dynamischer Effekte in produktionstechnischen Systemen" gefördert

Projektleitung: Prof. Dr. Engelbert Westkämper, Prof. Dr. Günter Radons

Der Einsatz der Wasserstrahltechnik in industriellen Anwendungen ist begrenzt durch eine starke Rillen- und Riefenbildung an der Unterkante der Schnittkerbe bei hohen Schnittgeschwindigkeiten. Ziel des Projektes ist es, durch die Verwendung von zeitlich hochauflösenden optischen, akustischen u. gravimetrischen Meßsystemen und einer Analyse der Strukturbildungsprozesse durch Methoden der nichtlinearen Dynamik zu einem erweiterten Prozessverständnis zu gelangen. Hierzu sollen dynamische raumzeitliche Vorgänge aus Versuchsdaten rekonstruiert und mit nichtlinearen Methoden modelliert werden, um daraus – neben den analytischen Modellen – empirische Modelle der Prozessdynamik ableiten zukönnen. Aus den gewonnenen Evolutionsgleichungen werden Strategien zur Optimierung des Prozesses entwickelt und verifiziert.

Die Schnittgeschwindigkeit und die Schnittqualität werden durch die Ausbildung von Riefen und Rillen an der Schnittkante bei hohen Vorschubgeschwindigkeiten begrenzt.

Analyse verborgener Diffusionsprozesse

Bis 2004 durch das interdisziplinäres DFG-Schwerpunktprogramm 1114 "Mathematische Methoden der Zeitreihenanalyse und digitalen Bildverarbeitung" gefördert
http://www.math.uni-bremen.de/zetem/DFG-Schwerpunkt/

Projektleitung: Prof. Dr. Günter Radons
Kontakt: Dr. Abdelhadi Benabdallah

Diffusionsprozesse, die kontinuierlich in Raum und Zeit stattfinden, können oft nicht direkt beobachtet werden, sondern nur vermittelt durch Funktionen, die den Mess- oder Beobachtungsprozess widerspiegeln. In dem Projekt sollen Methoden entwickelt werden, um solche "verborgenen" Diffusionsprozesse zu erschließen. Es basiert auf Erfahrungen im Bereich der Zeitreihenanalyse mit Hidden-Markov-Modellen, die in diskreter oder kontinuierlicher Zeit, aber bisher ausschließlich mit diskreten Zuständen formuliert werden. Die dort bekannten Konzepte sollen auf zeitlich und räumlich kontinuierliche Prozesse, wie sie häufig in physikalischen Systemen zu finden sind, erweitert werden. Bei den resultierenden verborgenen Diffusionsprozessen geht man davon aus, dass die diffundierende Zustandsvariable, deren Dynamik typischerweise durch Fokker-Planck- bzw. Langevin-Gleichungen beschrieben wird, nicht direkt beobachtet werden kann, sondern nur vermittels einer deterministischen oder stochastischen Beobachtungsfunktion. Aus Zeitreihen der beobachtbaren Variable soll durch Verallgemeinerungen des EM-Algorithmus eine Parameterschätzung des zugrunde liegenden Diffusionsprozesses ermöglicht werden. Von besonderem Interesse sind Fälle, bei denen der Wertebereich der Beobachtungsvariable, im Gegensatz zur diffundierenden Zustandsvariable, beschränkt bleibt.

Schematische Näherung eines verborgenen Diffusionsprozesses durch ein diskretes Modell

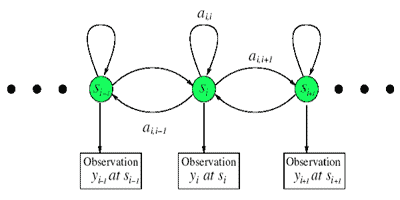
Als beispielhafte Anwendung der zu entwickelnden Methoden soll zunächst die Diffusion in einem eindimensionalen, periodischen Potential betrachtet werden, bei der die observierte Zeitreihe aus einer Sequenz von Potentialwerten der diffundierenden Zustandsvariable besteht, die zu deterministisch oder stochastisch verteilten Zeitpunkten gewonnen wurde. Erweiterungen bestehen in der Einbeziehung von Beobachtungsfehlern im Messprozess.

Methoden der Systemadaption

Bis 2002 durch den Sonderforschungsbereich 467 "Wandlungsfähige Unternehmensstrukturen für die variantenreiche Serienproduktion" (Stuttgart) finanziert
Projektbereich A "Grundlagen der Optimierung und Adaption"
Teilprojekt A1 "Methoden der Systemadaption"
http://www.sfb467.uni-stuttgart.de/

Projektleitung: Prof. Dr. Günter Radons

Zentrales Thema des Sonderforschungsbereiches ist der Übergang von eher starr organisierten Produktionssystemen zu wandlungsfähigen Produktionsnetzwerken. Das Teilprojekt A1 trägt mit der Erforschung neuer Konzepte für die kurz- und langfristige Adaption von Strukturen und Prozessen hierzu bei.

In der laufenden Förderperiode werden vernetzte Leistungseinheiten (LE), auch unter dynamischen Einflüssen, behandelt. Die zeitlich variierenden Einwirkungen können dabei durch die Wechselwirkung der LE selbst generiert oder extern (saisonbedingte Schwankungen, turbulentes Umfeld) verursacht sein. Diese Situation hat starke Parallelen zu koevolutionären Prozessen in der Natur. Letztere sind unter anderem Gegenstand der Forschungszweige "Artificial Life" und "Evolutionary Computation", die sich die Umsetzung von Konzepten der Evolutionsbiologie in technische Problemlösungsverfahren zum Ziel gesetzt hat.

Die Grafik stellt die beste Lösung des von uns entwickelten Genetischen Algorithmus für ein Facility Layout Problem mit 62 Departments dar. Die Departments clustern in acht Gruppen. Der koevolutionäre genetische Algorithmus erreicht diese Lösung in einigen Stunden, eine Rechenzeit, in der globale Optimierungsalgorithmen scheitern.